---

整数存储

原码、反码、补码

整数的2进制表示方法有三种，即原码、反码和补码
三种表示方法均有符号位和数值位两部分，符号位用0表示“正”，用1表示“负”。

有符号整数最高位的一位是被当做符号位，剩余的都是数值位。
无符号整数所有的位都是数值位

---

转换规则

正整数的原、反、补码都相同。
负整数的三种表示方法各不相同。

原码：直接将数值按照正负数的形式翻译成二进制得到的就是原码。
反码：将原码的符号位不变，其他位依次按位取反就可以得到反码。
补码：反码+1就得到补码。

正数：

对于int（整形），计算机会给内存开辟4个字节即32个比特来存放a。由于在此a是正数，第一位符号位为0，数值为5，转化为二进制就是101，存在最后。正数的原反补三码相同。

负数：

由于在此a是负数，在原码中，第一位是符号位，存放1。
反码：符号位不变，保持为1。其余位按位取反，即0变1，1变0.
补码：在反码的情况下加1。
而补码想要变回原码，也是相同的步骤，即先取反后加一。

数据与内存的关系

首先，我们在内存中存储的数据是以补码的形式存储的。我们用代码定义a，b为5和-5，然后观察其在内存中的值：

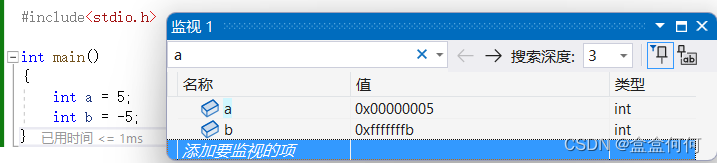
由于二进制实在难于分辨，所以编译器在向程序员呈现计算机存储的值的时候，会转为16进制。我们从上图中可见，a的存储是可以理解的，可b的值却不是-00000005。这个fffffffb其实就是-5的补码的16进制形式，由此可以证明，内存存储数据就是以补码的形式。
那为什么内存要存补码？

• 可以把符号与数值统一处理，把数字的正负放在码值中，不用额外区分。
• 可以使加法减法统一处理（CPU只有加法计算器）。

第一点其实是容易理解的，那为什么用补码可以统一加减法呢？我们以下面的代码为例：

以上代码中，计算机想要完成3 - 5，于是CPU将其转化为了3 + （-5），然后直接将补码相加，然后转回原码，得到的就是正确答案。

可见，虽然代码是减法，但是在计算机处理的时候，只做了加法运算。这样可以减少计算机硬件的消耗，只需要在CPU内部做好加法的硬件即可。

---

大小端字节序

讲完整数的存储后，我提出一个新的问题：int类型占用四个字节，请问这四个字节在内存中是从高到低，还是从低到高存储？这就涉及到了大小端字节序的问题。

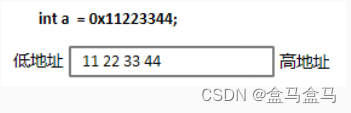
int a = 0x11223344;

变量a是十六进制的11223344，十六进制转二进制，每一位数字转为四位二进制，所以每两个十六进制数字占一个字节。上述代码中11，22，33，44各占一个字节。当一个变量占用多个字节，字节会区分高位与低位：

11为高位字节序
44为低位字节序

而在内存中一个变量的多个字节有两种存储顺序：

大端字节序：将一个数值的低位字节序存储到内存的高地址处

小端字节序：将一个数值的低位字节序存储到内存的低地址处

值得注意的是：大小端字节序并不取决于编译器，而取决于计算机的硬件实现。

接下来我们设计一个程序来检测我们的计算机是大端字节序还是小端字节序：
大小端存储，是发生在一个变量同时占用多个字节的情况下的，想要检测计算机的大小端，那就需要在一个变量内部区分出高地址与低地址。
而指针就有这个特性：指向某个变量的指针，其地址为该变量所有地址中最低的那个地址，这样我们把一个指向占用多个字节变量的指针强制转化为char*指针，就可以访问到其最低位的地址了。

代码如下：

int a = 1;
char* pa = (char*)&a;if (*pa == 0)printf("大端字节序\n");
else if (*pa == 1)printf("小端字节序\n");

以上代码中，我们定义了一个a = 1，那么a的十六进制就是0x 00 00 00 01，其低位字节序为01，高位字节序为00。我们利用char*指针取到低地址处的变量后，如果低地址为00，说明高位存储在了低地址，是大端字节序；如果低地址为01，说明低位存储在了低地址，是小端字节序。

---

浮点数存储

IEEE 754标准

在C语言中，浮点数的存储是基于IEEE 754标准来实现的。
IEEE 754规定：任何一个二进制浮点数V，都可以存储为以下形式：

V = (-1)^s × M × 2^E

• (-1)^s：表示符号位，当S = 0， V为正数；S = 1， V为负数
• M：表示有效数字，1 <= M < 2
• 2^E：表示指数位

接下来我详细讲解一下这套规则：
S：这个很好理解，即用于控制浮点数的正负

M：
一个二进制的浮点数，其一定由0与1构成，比如1011.0101这个浮点数，为了统一处理，我们==将所有浮点数的最左位1放在小数点左边，其余位放在小数点右边。

以下是一些示例：

1011.0101 -> 1.0110101
0.00001011 -> 1.011
1111111.11111 -> 1.11111111111
0.0001 -> 1.0

在这种转化下，M一定是1.xxxxx，所以有1 <= M < 2。

E：
经过上述转化，那就会发生小数点的偏移，为了矫正这个偏移量，于是存在了E。
比如1011.0101 -> 1.0110101这个过程，其小数点偏移了三位，那就有1011.0101 = 1.0110101 * 2 ^ 3，此时E就表示2的指数，E = 3。

再比如0.00001011 -> 1.011，0.00001011 = 1.011 * 2 ^ (-5)，此时E = -5。

理解了这套规则后，我们尝试转化一个数字：-5.0

-5.0，为负数，所以S = 1
5.0转化为二进制为：101.0
小数点左移两位：101.0 -> 1.01，故M = 1.01，E = 2
综上：-5.0 = -101.0 = (-1)¹ × 1.01 × 2²

---

存储过程

知道了浮点数的存储规则后，我们再看看这个数据是如何存放在内存中的。
想要存储一个浮点数，经过上述转换规则，也就是要存储S，M，E三个数据。

对于单精度浮点数float，第一位分配给S，为E分配了8个bit位，M分配了23个bit位：

对于双精度浮点数double，第一位分配给S，为E分配了11个bit位，M分配了52个bit位：

S：

直接判断浮点数正负，然后在第一位存入0 / 1 即可

M：

先前我们强调过，1.0 <= M < 2，即M一定是1.xxx的形式，所以小数点前第一位一定是1，所以可以省略掉M的第一位1，只存储小数点后面的数字。比如保存 1.01 只存储 01，小数点前的1被省略了

E：

对于float而言，其分配了8位bit存储E，所以E的存储范围是[0, 255]。但是科学计数法中，指数可以为负数，所以不能从0开始存储，于是给出一个中间数，用于调节正负。存入之前，先加上一个中间数保证所有的E都被转化为正数，当取出E使用的时候，再减去中间数
float的中间数是127，比如我们的E = -9，那么存储进内存的时候实际存储的是-9 + 127 = 118；如果E = 20，存储进内存的时候实际存储的是20 + 127 = 147。所以E的实际存储范围是：[-127, 128]
double同理，其中间数是1023，存入数据前要先加上这个中间数

---

取用过程

将浮点数从内存中取出来，其实就是以上过程的逆过程：

1. 先取出S，M，E

• 取M时，取到的是小数点后的数据，要再在小数点前面加上1
  比如从内存中取到的数据为：101101，那么M = 1.101101
• 取E时，要减掉中间数
  比如取到的数据为130，那么E = 130 -127 = 3

2. 根据 V = (-1)^s × M × 2^E 计算得到浮点数

以上是一般情况的取用，但是还有两种特殊情况：

• 当E为全0：

表⽰±0，以及接近于0的很⼩的数字。

• 当E为全1：

这时，如果有效数字M全为0，表⽰±⽆穷⼤（正负取决于符号位s）

---

数据的存储范围

此处以signed char为例，int，long等以此类推即可。
我们首先列举一下signed char类型可能存在的码值：

0000 0000(0)
0000 0001(1)
......
0111 1111(127)
1000 0000(?)
1000 0001(-127)
......
1111 1110(-2)
1111 1111(-1)

以上列举中，以4bit为一单位，共8bit，即1字节。根据原码与补码的转化，以上规则应该十分清晰，唯一的问题就是1000 0000是什么？
先根据一般的转化规则：

1000 0000以1开头，说明这是一个负数，转原码需要取反 +1
取反：1111 1111
+1：1 0000 0000，可以发现此时发生了进位，截断为8位就是0000 0000，也就是0
可是我们的0已经有0000 0000来表示了，1000 0000再表示0就显得多余了
于是规定：1000 0000用于表示-128
这也是符合一定逻辑的，因为你会发现1000 0000 + 1 = 1000 0001，也就是1000 0000 + (-1) = -127，那么1000 0000表示为-128也就是合理的了

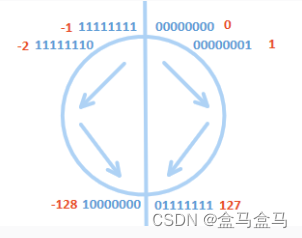
以上图片中，顺时针走下去，下一个数字就是上一个数字 +1，比如1 = 0 + 1，-1 = -2 +1；

在边界处有两个特例：

-1 + 1 = 0这个计算符合数学逻辑，但不是直接计算得到的，因为-1的补码为1111 1111，0的补码为0000 0000。-1 + 1 = 1111 1111 + 1 = 1 0000 0000 ，由于发生了进位，此时有9位数据，要发生一次截断，导致1 0000 0000变成了0000 0000，所以最后得到了0。

127 + 1 = -128这是一个特例，因为我们规定了1000 0000为-128，所以此处会发生这个不符合数学逻辑的情况。

总结：

• signed char的存储范围是：[-128, 127]。
• 当signed char发生了这个范围以外的计算，要注意超过127的数值，会从-128开始重新计算，因为127 + 1 = -128。

---