傅里叶分析不仅仅是一个数学工具,更是一种可以彻底颠覆一个人以前世界观的思维模式。
一、什么是频域 时域
时域是信号在时间轴随时间变化的总体概括;频域是把时域波形的表达式做傅立叶等变化得到复频域的表达式,所画出的波形就是频谱图,是描述频率变化和幅度变化的关系。
示波器用来看时域内容,频普仪用来看频域内容。
时域:
时间域,time domain。自变量是时间,即横轴是时间,纵轴是信号的变化。其动态信号x(t ) 是描述信号在不同时刻取值的函数。
频域:
频率域,frequency domain。自变量是频率,即横轴是频率,纵轴是该频率信号的幅度,也就是通常说的频谱图。频谱图描述了信号的频率结构及频率与该频率信号幅度的关系。
时域分析与频域分析:
对信号进行时域分析时,有时一些信号的时域参数相同,但并不能说明信号就完全相同。因为信号不仅随时间变化,还与频率、相位等信息有关,这就需要进一步分析信号的频率结构,并在频率域中对信号进行描述。动态信号从时间域变换到频率域,主要通过傅立叶级数和傅立叶变换等来实现。很简单,时域分析的函数是参数是t,也就是y=f(t );频域分析时,参数是w,也就是y=F(w ) 两者之间可以互相转化。时域函数通过傅立叶或者拉普拉斯变换就变成了频域函数。

傅里叶告诉我们,任何周期函数,都可以看作是不同振幅,不同相位正弦波的叠加。
二、傅里叶级数(Fourier Series)的频谱

正弦波就是一个圆周运动在一条直线上的投影。所以频域的基本单元也可以理解为一个始终在旋转的圆。
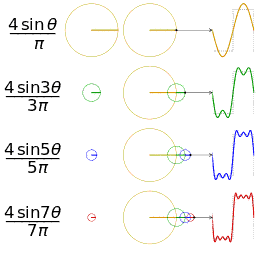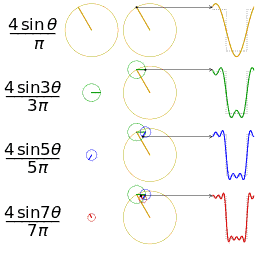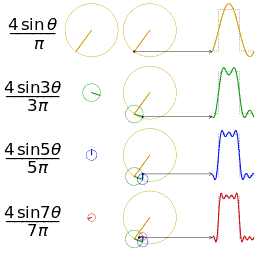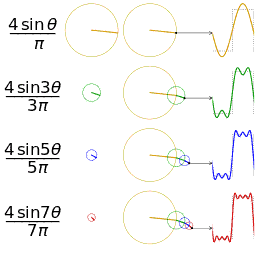
Fourier series square wave circles animation 傅里叶级数方波圆动画
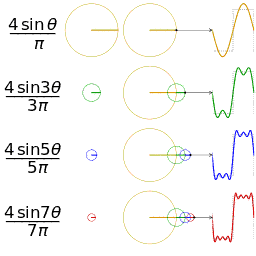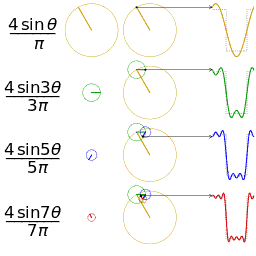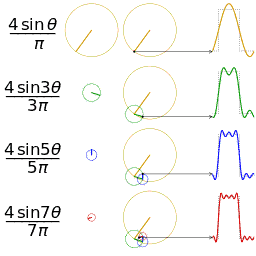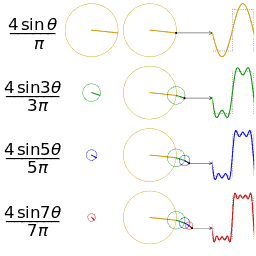
Fourier series sawtooth wave circles animatio 傅立叶级数锯齿波圆动画

介绍完了频域的基本组成单元,我们就可以看一看一个矩形波,在频域里的另一个模样了: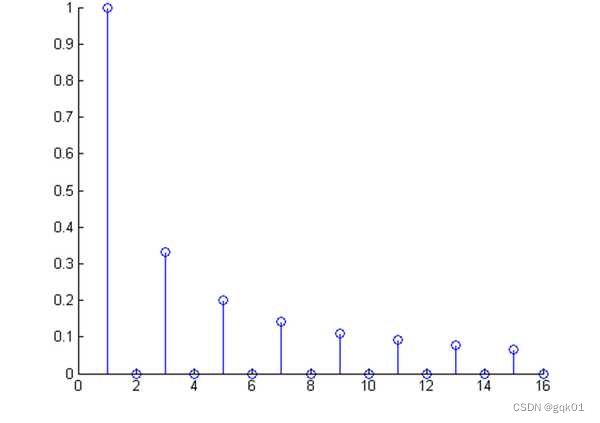
这是什么奇怪的东西?
这就是矩形波在频域的样子,是不是完全认不出来了?教科书一般就给到这里然后留给了读者无穷的遐想,以及无穷的吐槽,其实教科书只要补一张图就足够了:频域图像,也就是俗称的频谱,就是——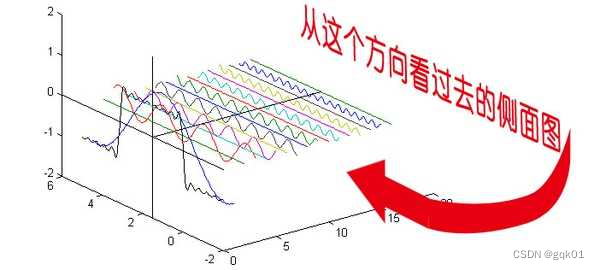
再清楚一点:
可以发现,在频谱中,偶数项的振幅都是0,也就对应了图中的彩色直线。振幅为 0 的正弦波。

Fourier series and transform 傅里叶级数及其变换
想象一下,世界上每一个看似混乱的表象,实际都是一条时间轴上不规则的曲线,但实际这些曲线都是由这些无穷无尽的正弦波组成。我们看似不规律的事情反而是规律的正弦波在时域上的投影,而正弦波又是一个旋转的圆在直线上的投影。那么你的脑海中会产生一个什么画面呢?
三、傅里叶级数(Fourier Series)的相位谱
所以很多在时域看似不可能做到的数学操作,在频域相反很容易。这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分,这在工程上称为滤波,是信号处理最重要的概念之一,只有在频域才能轻松的做到。
再说一个更重要,但是稍微复杂一点的用途——求解微分方程。(这段有点难度,看不懂的可以直接跳过这段)微分方程的重要性不用我过多介绍了。各行各业都用的到。但是求解微分方程却是一件相当麻烦的事情。因为除了要计算加减乘除,还要计算微分积分。而傅里叶变换则可以让微分和积分在频域中变为乘法和除法,大学数学瞬间变小学算术有没有。
继续说相位谱:
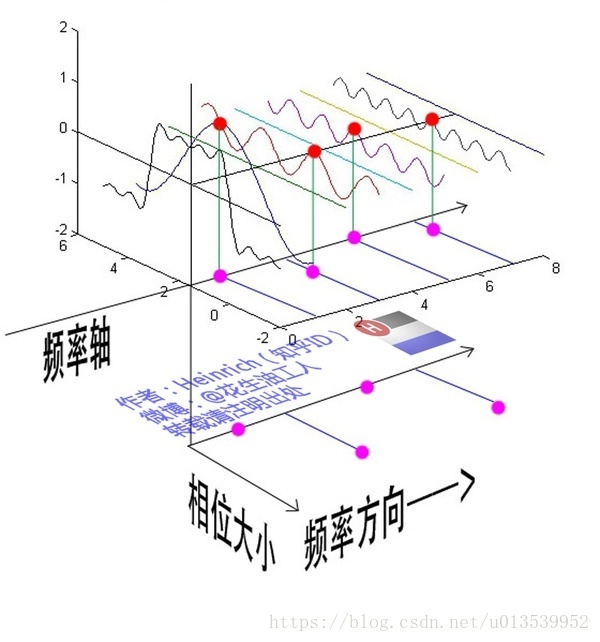
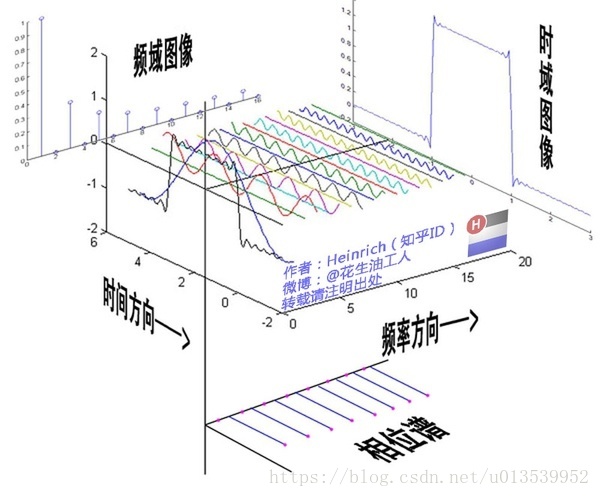
通过时域到频域的变换,我们得到了一个从侧面看的频谱,但是这个频谱并没有包含时域中全部的信息。因为频谱只代表每一个对应的正弦波的振幅是多少,而没有提到相位。基础的正弦波A.sin(wt+θ)中,振幅,频率,相位缺一不可,不同相位决定了波的位置,所以对于频域分析,仅仅有频谱(振幅谱)是不够的,我们还需要一个相位谱。那么这个相位谱在哪呢?我们看下图,这次为了避免图片太混论,我们用7个波叠加的图。
鉴于正弦波是周期的,我们需要设定一个用来标记正弦波位置的东西。在图中就是那些小红点。小红点是距离频率轴最近的波峰,而这个波峰所处的位置离频率轴有多远呢?为了看的更清楚,我们将红色的点投影到下平面,投影点我们用粉色点来表示。当然,这些粉色的点只标注了波峰距离频率轴的距离,并不是相位。
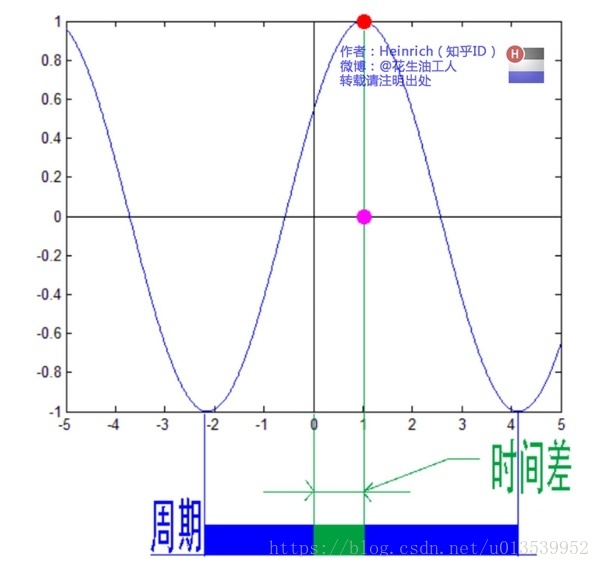
这里需要纠正一个概念:时间差并不是相位差。如果将全部周期看作2Pi或者360度的话,相位差则是时间差在一个周期中所占的比例。我们将时间差除周期再乘2Pi,就得到了相位差。
在完整的立体图中,我们将投影得到的时间差依次除以所在频率的周期,就得到了最下面的相位谱。所以,频谱是从侧面看,相位谱是从下面看。下次偷看女生裙底被发现的话,可以告诉她:“对不起,我只是想看看你的相位谱。”
注意到,相位谱中的相位除了0,就是Pi。因为cos(t+Pi)=-cos(t),所以实际上相位为Pi的波只是上下翻转了而已。对于周期方波的傅里叶级数,这样的相位谱已经是很简单的了。另外值得注意的是,由于cos(t+2Pi)=cos(t),所以相位差是周期的,pi和3pi,5pi,7pi都是相同的相位。人为定义相位谱的值域为(-pi,pi],所以图中的相位差均为Pi。
最后来一张大集合:
四、傅里叶变换(Fourier Tranformation)
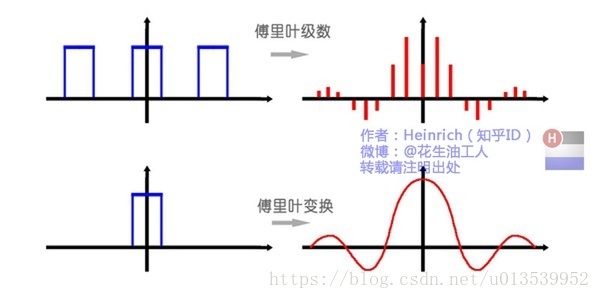
傅里叶级数的本质是将一个周期的信号分解成无限多分开的(离散的)正弦波,但是宇宙似乎并不是周期的。
傅里叶变换,则是将一个时域非周期的连续信号,转换为一个在频域非周期的连续信号。
算了,还是上一张图方便大家理解吧:
或者我们也可以换一个角度理解:傅里叶变换实际上是对一个周期无限大的函数进行傅里叶变换。
所以说,钢琴谱其实并非一个连续的频谱,而是很多在时间上离散的频率,但是这样的一个贴切的比喻真的是很难找出第二个来了。
因此在傅里叶变换在频域上就从离散谱变成了连续谱。那么连续谱是什么样子呢?
从频率较高的方向看。
以上是离散谱,那么连续谱是什么样子呢?
尽情的发挥你的想象,想象这些离散的正弦波离得越来越近,逐渐变得连续……
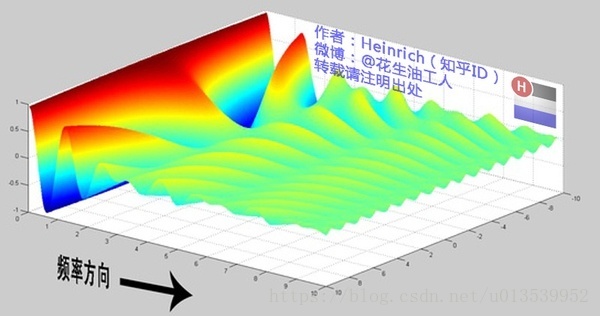
直到变得像波涛起伏的大海:
很抱歉,为了能让这些波浪更清晰的看到,我没有选用正确的计算参数,而是选择了一些让图片更美观的参数,不然这图看起来就像屎一样了。
不过通过这样两幅图去比较,大家应该可以理解如何从离散谱变成了连续谱的了吧?原来离散谱的叠加,变成了连续谱的累积。所以在计算上也从求和符号变成了积分符号。
五、 欧拉公式
虚数i这个概念大家在高中就接触过,但那时我们只知道它是-1 的平方根,可是它真正的意义是什么呢?
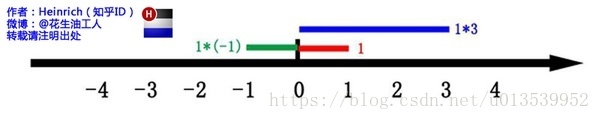
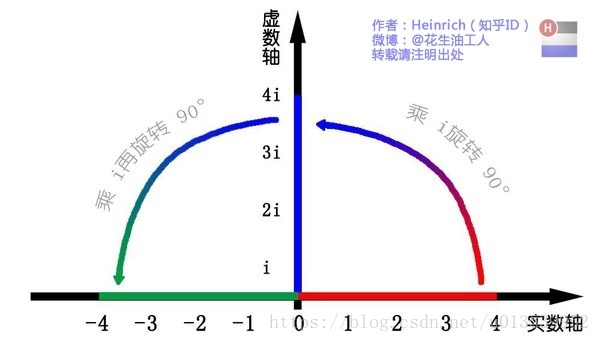
这里有一条数轴,在数轴上有一个红色的线段,它的长度是1。当它乘以 3 的时候,它的长度发生了变化,变成了蓝色的线段,而当它乘以-1 的时候,就变成了绿色的线段,或者说线段在数轴上围绕原点旋转了 180 度。
我们知道乘-1 其实就是乘了两次 i 使线段旋转了 180 度,那么乘一次 i 呢——答案很简单——旋转了 90 度。
同时,我们获得了一个垂直的虚数轴。实数轴与虚数轴共同构成了一个复数的平面,也称复平面。这样我们就了解到,乘虚数i的一个功能——旋转。
现在,就有请宇宙第一耍帅公式欧拉公式隆重登场——
这个公式在数学领域的意义要远大于傅里叶分析,但是乘它为宇宙第一公式是因为它的特殊形式——当x等于 Pi 的时候。
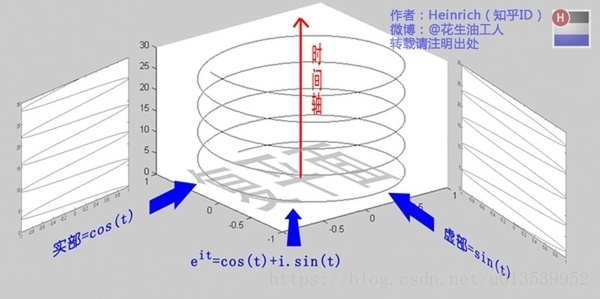
这个公式关键的作用,是将正弦波统一成了简单的指数形式。我们来看看图像上的涵义:
欧拉公式所描绘的,是一个随着时间变化,在复平面上做圆周运动的点,随着时间的改变,在时间轴上就成了一条螺旋线。如果只看它的实数部分,也就是螺旋线在左侧的投影,就是一个最基础的余弦函数。而右侧的投影则是一个正弦函数。
关于复数更深的理解,大家可以参考:
复数的物理意义是什么?
六、指数形式的傅里叶变换
有了欧拉公式的帮助,我们便知道:正弦波的叠加,也可以理解为螺旋线的叠加在实数空间的投影。而螺旋线的叠加如果用一个形象的栗子来理解是什么呢?
光波
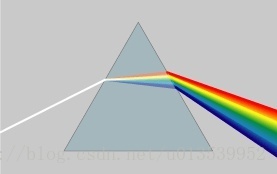
高中时我们就学过,自然光是由不同颜色的光叠加而成的,而最著名的实验就是牛顿师傅的三棱镜实验:
所以其实我们在很早就接触到了光的频谱,只是并没有了解频谱更重要的意义。
但不同的是,傅里叶变换出来的频谱不仅仅是可见光这样频率范围有限的叠加,而是频率从 0 到无穷所有频率的组合。
这里,我们可以用两种方法来理解正弦波:
第一种前面已经讲过了,就是螺旋线在实轴的投影。
另一种需要借助欧拉公式的另一种形式去理解:
将以上两式相加再除2,得到:
这个式子可以怎么理解呢?
我们刚才讲过,e^(it)可以理解为一条逆时针旋转的螺旋线,那么e^(-it)则可以理解为一条顺时针旋转的螺旋线。而 cos (t)则是这两条旋转方向不同的螺旋线叠加的一半,因为这两条螺旋线的虚数部分相互抵消掉了!
举个例子的话,就是极化方向不同的两束光波,磁场抵消,电场加倍。这里,逆时针旋转的我们称为正频率,而顺时针旋转的我们称为负频率(注意不是复频率)。
好了,刚才我们已经看到了大海——连续的傅里叶变换频谱,现在想一想,连续的螺旋线会是什么样子:
想象一下再往下翻:
是不是很漂亮?
你猜猜,这个图形在时域是什么样子?
哈哈,是不是觉得被狠狠扇了一个耳光。数学就是这么一个把简单的问题搞得很复杂的东西。
顺便说一句,那个像大海螺一样的图,为了方便观看,我仅仅展示了其中正频率的部分,负频率的部分没有显示出来。
如果你认真去看,海螺图上的每一条螺旋线都是可以清楚的看到的,每一条螺旋线都有着不同的振幅(旋转半径),频率(旋转周期)以及相位。而将所有螺旋线连成平面,就是这幅海螺图了。
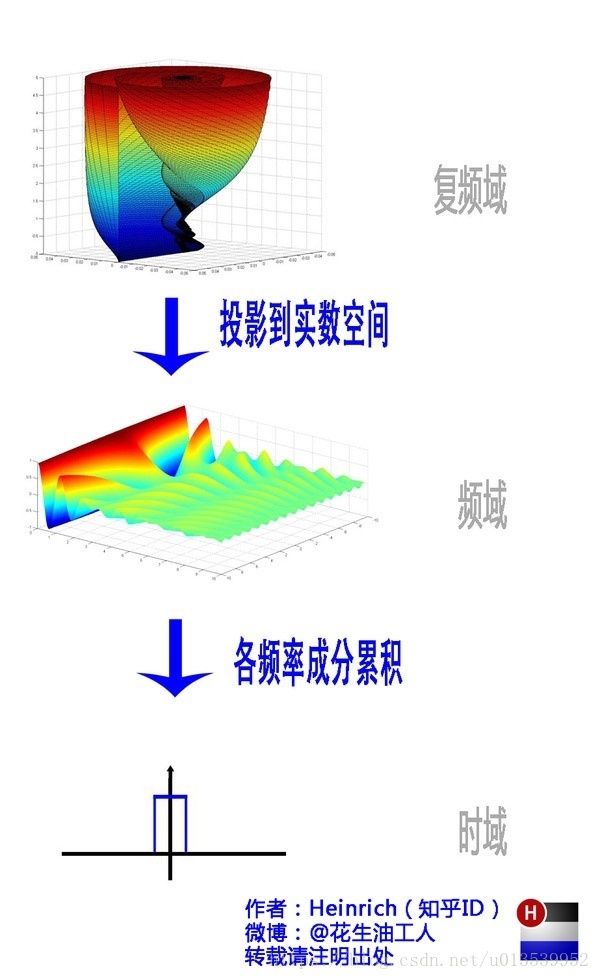
好了,讲到这里,相信大家对傅里叶变换以及傅里叶级数都有了一个形象的理解了,我们最后用一张图来总结一下:

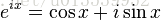
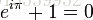
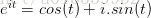
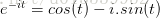
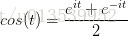

:Docker Desktop原生图形化管理)



)













