参考：
[1] 张振虎博客
[2] https://www.bilibili.com/video/BV1s8411i7cU/?spm_id_from=333.788&vd_source=9e9b4b6471a6e98c3e756ce7f41eb134
[3] https://zhuanlan.zhihu.com/p/660518657
[4] https://zhuanlan.zhihu.com/p/640631667

1 前言

我们在DDPM或DDIM生成图像时是通常是不可控的，因为它是由一张随即高斯噪声一步步去噪得到生成图像。如果我们想要这个过程是可控的话，最直观的一个做法就是在生成过程中加上一个条件$y$,既整个过程的变为：
$$p(x_{1:T}|x_0,y)$$
接下来就是讨论加上了条件$y$对于公式有无影响。

首先扩散模型遵循马尔科夫链性质，所以我们可以得出：
$$p(x_t|x_{t-1},y):=p(x_t|x_{t-1})$$
基于这一事实，我们还可以推出：
$$\begin{array}{rl}\hat{q}(x_t|x_{t-1})& ={\int }_y\hat{q}(x_t,y|x_{t-1})dy\\ & ={\int }_y\hat{q}(x_t|y,x_{t-1})\hat{q}(y|x_{t-1})dy\\ & ={\int }_y\hat{q}(x_t|x_{t-1})\hat{q}(y|x_{t-1})dy\\ & =\hat{q}(x_t|x_{t-1})=\hat{q}(x_t|x_{t-1},y)\end{array}$$

同样用全概率公式，可以推出：

所以我们可以断论：加上条件$y$ 对前向过程毫无影响

2 Classifier Guidance

逆向过程有如下公式：
$$\hat{p}(x_{t-1}|x_t,y)=\frac{\hat{p}(x_{t-1}|x_t)\hat{p}(y|x_{t-1},x_t)}{\hat{p}(y|x_t)}$$
其中分母和$x_{t-1}$毫无关系，所以分母可以看作是常数$C$。
而我们知道加上条件对于扩散过程是没有影响的，所以我们还已知：
$$\begin{gathered} \hat{q}(x_t|x_{t-1},y)=q(x_t|x_{t-1}) \\ \hat{q}(x_0)=q(x_0) \\ \hat{q}(x_{1:T}|x_0,y)=\prod _{t=1}^{T}q(x_t|x_{t-1},y) \end{gathered}$$

现在我们未知的是$\hat{p}(x_{t-1}|x_t)和\hat{p}(y|x_{t-1},x_t)$，现在来推导这两项：

1）推导$\hat{p}(x_{t-1}|x_t)$
根据贝叶斯公式，我们有：
$$\hat{p}(x_{t-1}|x_t)=\frac{\hat{p}(x_t|x_{t-1})\hat{p}(x_{t-1})}{\hat{p}(x_t)}$$
我们已知条件$y$ 对扩散过程不影响（可以通过全概率公式推出），所以我们有
$$\hat{p}(x_t|x_{t-1})=p(x_t|x_{t-1})$$
我们同样可以由全概率公式推出：
$$\hat{p}(x_t)=p(x_t)$$

所以
$$\hat{p}(x_{t-1}|x_t)=\frac{p(x_t|x_{t-1})p(x_{t-1})}{p(x_t)}$$

2）推导$\hat{p}(y|x_{t-1},x_t)$

根据贝叶斯公式，有：
$$\hat{p}(y|x_{t-1},x_t)=\frac{\hat{p}(x_t|y,x_{t-1})\hat{p}(y|x_{t-1})}{\hat{p}(x_t|x_{t-1})}$$
根据马尔可夫链性质，所以约去分子的第一项和分母，所以得到
$$\hat{p}(y|x_{t-1},x_t)=\hat{p}(y|x_{t-1})$$

3）终极目标

所以我们的公式此刻为：
$$\hat{p}(x_{t-1}|x_t,y)=\frac{q(x_{t-1}|x_t)q(y|x_{t-1})}{q(y|x_t)}=C\ast q(x_{t-1}|x_t)\ast q(y|x_{t-1})$$
其中第一项是常数，第二项为DDPM的目标，第三项既为分类器输出概率（根据$x_{t-1}$输出类别标签$y$）

4）问题与进一步推导
我们此刻为$t$时刻，我们是不可以得出$x_{t-1}$的。但是我们只是每一次从$x_t$到$x_{t-1}$实际上只做了很微小的变化，所以我们是可以近似$x_{t-1}$的，用泰勒展开式去近似。

我们有
$$log{p}_{\theta }(x_{t-1}|x_t)=-\frac{1}{2}\frac{(x_{t-1}-\mu {)}^2}{\Sigma }$$
而$\Sigma$是很小的，我们可以理解为$x_{t-1}$出现在$x_t$的附近，而$x_t$约等于期望
所以令$x_{t-1}=\mu$

有
$$log{p}_{\varphi }(y|x_{t-1})=log{p}_{\varphi }(y|x_{t-1}{)}_{|x_{t-1}=\mu }+(x_{t-1}-\mu ){\nabla }_{x_{t-1}}log{p}_{\varphi }(y|x_{t-1}{)}_{|x_{t-1}=\mu }+o(高阶)$$
又第一项和后面的高阶项相当于常数，所以约等于
$$log{p}_{\varphi }(y|x_{t-1})=(x_{t-1}-\mu ){\nabla }_{x_{t-1}}log{p}_{\varphi }(y|x_{t-1}{)}_{|x_{t-1}=\mu }$$

我们将两个对数相加，一番推导后（我不会）可以得到
$$logp(x_{t-1}|x_t,y)\sim N(\mu +\Sigma \nabla log{p}_{\varphi }(y|x_{t-1}{)}_{|x_{t-1}=\mu })$$
既采样时，有
$$x_{t-1}=\mu +\Sigma \nabla +\Sigma ϵ$$
其中$\nabla$为分类器的梯度，所以这么一番推导，我们只是在最后的采样公式里加了一个引导方向的梯度项。
但有个缺点就是，DDIM的$\Sigma =0$，那么不就没用了。
而且还有两个缺点：

1. 还要预训练一个分类器模型
2. 只能生成分类器训练集所有的类别

5）用能量函数(score-base function)做进一步泛化

已知
$$s={\nabla }_{x_t}logp(x_t)$$
我们已知梯度和噪声的关系为：
$${\nabla }_{x_t}logp(x_t)=\frac{-ϵ}{\sqrt{1-{\bar{\alpha }}_t}}$$
如果没有classifier guidance，那么我们的神经网络想要预测的就是
$${\nabla }_{x_t}log{p}_{\theta }(x_t)=\frac{-{ϵ}_{\theta }}{\sqrt{1-{\bar{\alpha }}_t}}$$
现在加上classifier guidance,也就是加上了$\nabla log{p}_{\theta }(y|x_t)$，假设其值为$g$（为了方便，他就是分类器梯度）

其实我们神经网络实际上是预测：
$$\frac{-{ϵ}_{\theta }}{\sqrt{1-{\bar{\alpha }}_t}}+g$$

我们设其在预测
$$\frac{-{ϵ}^{\prime }}{\sqrt{1-{\bar{\alpha }}_t}}$$

将其取等式，然后做变换，再加上一个强度因子$w$，得到
$${ϵ}^{\prime }={ϵ}_{\theta }-w\sqrt{1-{\bar{\alpha }}_t}\nabla log{p}_{\varphi }(y|x_t)$$
也就是说，我们只需要在预测的噪声上加上一点扰动即可。而扰动项为分类器的梯度。

6）纯能量函数角度推导

原论文的伪代码的两个算法也是我们推导的：

7）不严谨代码理解

classifier_model = ...  # 加载一个训好的图像分类模型
y = 1  # 生成类别为 1 的图像，假设类别 1 对应“狗”这个类
guidance_scale = 7.5  # 控制类别引导的强弱，越大越强
input = get_noise(...)  # 从高斯分布随机取一个跟输出图像一样 shape 的噪声图for t in tqdm(scheduler.timesteps):# 用 unet 推理，预测噪声with torch.no_grad():noise_pred = unet(input, t).sample# 用 input 和预测出的 noise_pred 和 x_t 计算得到 x_t-1input = scheduler.step(noise_pred, t, input).prev_sample# classifier guidance 步骤class_guidance = classifier_model.get_class_guidance(input, y)input += class_guidance * guidance_scals  # 把梯度加上去

3 Classifier Free Guidance

我们知道对于classifier guidance最主要的限制就是分类器！CFG的方法就是直接将条件$y$也加到模型中直接训练，而不用在训练一个分类器了，这样相当于训练了一个隐式的分类器，也就是训练了无条件生成模型和有条件生成模型，只不过这两个模型融合在同一个生成模型里。数学推导如下：

不严谨代码理解

clip_model = ...  # 加载一个官方的 clip 模型text = "一只狗"  # 输入文本
text_embeddings = clip_model.text_encode(text)  # 编码条件文本
empty_embeddings = clip_model.text_encode("")  # 编码空文本
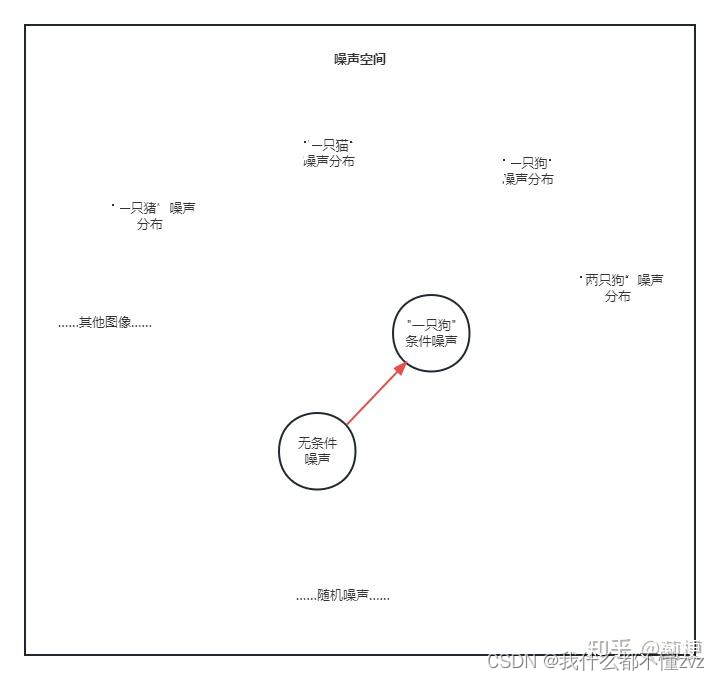
text_embeddings = torch.cat(empty_embeddings, text_embeddings)  # 把它俩 concate 到一起作为条件input = get_noise(...)  # 从高斯分布随机取一个跟输出图像一样 shape 的噪声图for t in tqdm(scheduler.timesteps):# 用 unet 推理，预测噪声with torch.no_grad():# 这里同时预测出了有文本的和空文本的图像噪声noise_pred = unet(input, t, encoder_hidden_states=text_embeddings).sample# Classifier-Free Guidance 引导noise_pred_uncond, noise_pred_text = noise_pred.chunk(2)  # 拆成无条件和有条件的噪声# 把【“无条件噪声”指向“有条件噪声”】看做一个向量，根据 guidance_scale 的值放大这个向量# （当 guidance_scale = 1 时，下面这个式子退化成 noise_pred_text）noise_pred = noise_pred_uncond + guidance_scale * (noise_pred_text - noise_pred_uncond)# 用预测出的 noise_pred 和 x_t 计算得到 x_t-1input = scheduler.step(noise_pred, t, input).prev_sample