利用一个简单的实例来介绍什么事线性规划，假设如果有一家巧克力工厂需要生产两种不同类型的巧克力，分别是类型A和类型B，两种巧克力用到的原材料是一样的，都是使用牛奶和可可两种材料，主要的区别是在与这两种原料的配料比区别，而对于类型A巧克力，生产一单位的巧克力会需要两单元的牛奶和三单元的可可，而对于类型B巧克力，生产一单元的巧克力会需要1单元的牛奶和2单元的可可。而假设现在如果共产会有原料5单元的牛奶和12单元的可可，此时类型A的巧克力每单元的售价是6元，类型B的巧克力每单元的售价是5元，如果为了获得最大化的销售利润，工厂需要考虑如何分配生产原料区生产不同的巧克力。

对于这个问题，如果使用X来表示生产的类型A巧克力的数量，用Y来表示生产类型B的巧克力的数量，那么利润的函数就是P（X,Y）=6X+5*Y，目的是为了找到X，Y，使得利润函数最大化，也就是满足：

添加图片注释，不超过 140 字（可选）

这里的主要存在的问题是X和Y不可以随意的设置，这两个值收到了原料数量的限制，生产这两种巧克力所需要的牛奶总量不能超过五单元，同时所需要的可可的数量总和不能超过12单元，于是就会有X和Y还需要满足条件：

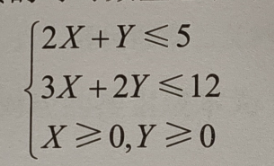
添加图片注释，不超过 140 字（可选）

在满足以上两个提哦啊见的情况下解决这个实际问题所用到的算法也就是线性规划思想的算法，而用数学的方式来表达就是要优化一组线性函数，同时函数中的变量必须遵守一系列不等式约束。

给定一组变量x1...xn，存在一组对应的参数a1....an，它们的线性组合函数:

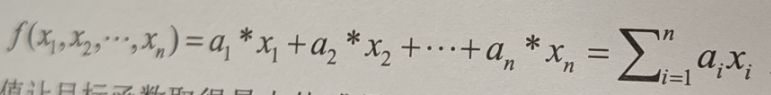
添加图片注释，不超过 140 字（可选）

这是想要最优化的目标函数，要找到一组变量值让目标函数取得最大值或最小值，同时这些变量还必须满足一系列不等式约束，也就是满足：

添加图片注释，不超过 140 字（可选）

找到满足条件的变量值的方法就是线性规划。