贪心算法章节理论基础：

https://programmercarl.com/%E8%B4%AA%E5%BF%83%E7%AE%97%E6%B3%95%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html

738.单调递增的数字

题目链接：https://leetcode.cn/problems/monotone-increasing-digits/

思路：

题目要求小于等于N的最大单调递增的整数，从后向前遍历，比如322来说，332 -> 329 -> 299。首先当前数字arr[i]–，然后最后一位给9。

要注意一个点就是，不能直接赋值成9，这里用的是一个start来保存位置，因为比如100，按我们刚刚的算法，他的结果是9，而不是99了。要注意一下这个地方。

class Solution {public int monotoneIncreasingDigits(int n) {// 从最后一位开始char[] arr = String.valueOf(n).toCharArray();int start = arr.length;for(int i=arr.length-2;i>=0;i--){if(arr[i] > arr[i + 1]){// arr[i+1] = '9';start = i + 1;arr[i]--;   // 当前位置减少1}}// 100 -> 99for(int i=start;i < arr.length;i++){arr[i] = '9';}return Integer.parseInt(String.valueOf(arr));}
}

968.监控二叉树

题目链接：https://leetcode.cn/problems/binary-tree-cameras/description/

思路：

摄像头可以覆盖上中下三层，如果把摄像头放在叶子节点上，就浪费的一层的覆盖。

所以我们要从下往上看，局部最优：让叶子节点的父节点安摄像头，所用摄像头最少，整体最优：全部摄像头数量所用最少！

可以使用后序遍历也就是左右中的顺序，这样就可以在回溯的过程中从下到上进行推导了。

下面，来看看这个状态应该如何转移，先来看看每个节点可能有几种状态：

有如下三种：

• 该节点无覆盖
• 本节点有摄像头
• 本节点有覆盖

我们分别有三个数字来表示：

0：该节点无覆盖
1：本节点有摄像头
2：本节点有覆盖

为了让摄像头数量最少，我们要尽量让叶子节点的父节点安装摄像头，这样才能摄像头的数量最少。

因为在遍历树的过程中，就会遇到空节点，那么问题来了，空节点究竟是哪一种状态呢？ 空节点表示无覆盖？ 表示有摄像头？还是有覆盖呢？

空节点不能是无覆盖的状态，这样叶子节点就要放摄像头了，空节点也不能是有摄像头的状态，这样叶子节点的父节点就没有必要放摄像头了，所以空节点的状态只能是有覆盖，这样就可以在叶子节点的父节点放摄像头了。

那么递归的终止条件应该是遇到了空节点，此时应该返回2（有覆盖）。

// 空节点，该节点有覆盖
if (cur == NULL) return 2;

主要有如下四类情况：

情况1：左右节点都有覆盖
左孩子有覆盖，右孩子有覆盖，那么此时中间节点应该就是无覆盖的状态了。

情况2：左右节点至少有一个无覆盖的情况
如果是以下情况，则中间节点（父节点）应该放摄像头.

情况3：左右节点至少有一个有摄像头
如果是以下情况，其实就是 左右孩子节点有一个有摄像头了，那么其父节点就应该是2（覆盖的状态）.

情况4：头结点没有覆盖
以上都处理完了，递归结束之后，可能头结点 还有一个无覆盖的情况。

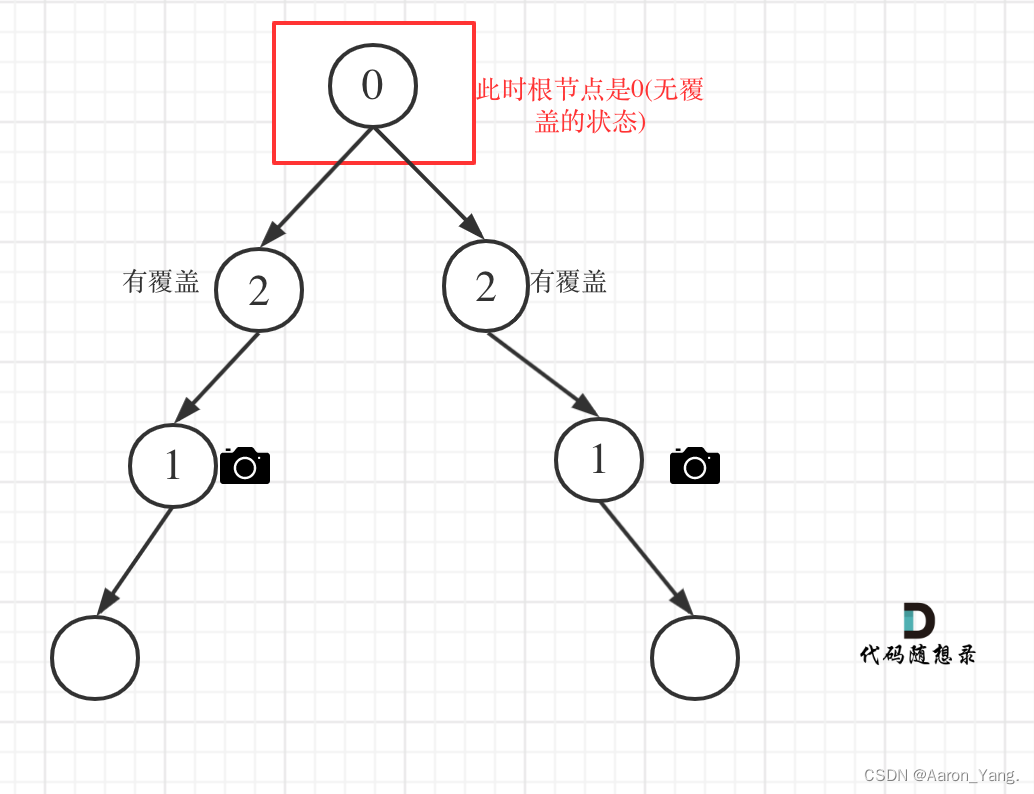
所以递归结束之后，还要判断根节点，如果没有覆盖，result++。

class Solution {public List<Integer> partitionLabels(String s) {int[] arr = new int[26];int len = s.length();// 统计每一个字符最后出现的位置for(int i = 0;i<len;i++){char c = s.charAt(i);arr[c-'a'] = i+1;}int left = 0;int right = 0;List<Integer> list = new LinkedList<>();for(int i=0;i<len;i++){// 找到字符最远的右边界right = Math.max(right,arr[s.charAt(i)-'a']);   if(right == i+1){list.add(right - left);left = right;}}return list;}
}