自编码器(Auto-Encoder)是学一个特征能够代表输入的图像
而VAE则为数据的隐变量加上先验——将隐变量限制为一个标准正态分布,也就是学一个具有代表性的分布
Abstract
How can we perform efficient inference and learning in directed probabilistic models, in the presence of continuous latent variables with intractable posterior distributions, and large datasets? We introduce a stochastic variational inference and learning algorithm that scales to large datasets and, under some mild differentiability conditions, even works in the intractable case. Our contributions are two-fold. First, we show that a reparameterization of the variational lower bound yields a lower bound estimator that can be straightforwardly optimized using standard stochastic gradient methods. Second, we show that for i.i.d. datasets with continuous latent variables per datapoint, posterior inference can be made especially efficient by fitting an approximate inference model (also called a recognition model) to the intractable posterior using the proposed lower bound estimator.Theoretical advantages are reflected in experimental results.
翻译:
我们如何在有连续潜在变量和难以处理的后续分布的定向概率模型中进行有效的推理和学习?我们引入了一种随机变分推理和学习算法,该算法可扩展到大型数据集,并且在一些温和的可微分性条件下,甚至在难以处理的情况下也能工作。我们的贡献有两个方面。首先,我们展示了对变分下界的重新参数化产生了一个下界估计器,该估计器可以使用标准的随机梯度方法直接优化。其次,我们显示对于每个数据点都有连续潜在变量的独立同分布数据集,可以通过使用提出的下界估计器将近似推理模型(也称为识别模型)拟合到难以处理的后续分布,从而使后验推理变得特别高效。理论优势在实验结果中得到了体现。
总结:
(1)通过对变分下界的重新参数化,可以将其转化为一个可使用标准随机梯度方法直接优化的形式
(2)使用提出的下界估计器可以将近似推理模型拟合到难以处理的后续分布
Introduction
How can we perform efficient approximate inference and learning with directed probabilistic models whose continuous latent variables and/or parameters have intractable posterior distributions? The variational Bayesian (VB) approach involves the optimization of an approximation to the intractable posterior. Unfortunately, the common mean-field approach requires analytical solutions of expectations w.r.t. the approximate posterior, which are also intractable in the general case. We show how a reparameterization of the variational lower bound yields a simple differentiable unbiased estimator of the lower bound; this SGVB (Stochastic Gradient Variational Bayes) estimator can be used for efficient approximate posterior inference in almost any model with continuous latent variables and/or parameters, and is straightforward to optimize using standard stochastic gradient ascent techniques.
For the case of an i.i.d. dataset and continuous latent variables per datapoint, we propose the AutoEncoding VB (AEVB) algorithm. In the AEVB algorithm we make inference and learning especially efficient by using the SGVB estimator to optimize a recognition model that allows us to perform very efficient approximate posterior inference using simple ancestral sampling, which in turn allows us to efficiently learn the model parameters, without the need of expensive iterative inference schemes (such as MCMC) per datapoint. The learned approximate posterior inference model can also be used for a host of tasks such as recognition, denoising, representation and visualization purposes. When a neural network is used for the recognition model, we arrive at the variational auto-encoder.
翻译:
我们如何在使用具有难以处理的后续分布的连续潜在变量和/或参数的定向概率模型中进行有效的近似推理和学习?变分贝叶斯(VB)方法涉及优化难以处理的后验的近似。不幸的是,常见的均值场方法需要解析地解决关于近似后验的期望,这在一般情况下也是难以处理的。我们展示了如何通过对变分下界的重新参数化得到一个简单、可微分的无偏下界估计器;这个SGVB(随机梯度变分贝叶斯)估计器可以用于几乎任何具有连续潜在变量和/或参数的模型的有效的近似后验推理,并且可以简单地使用标准的随机梯度上升技术进行优化。
对于独立同分布数据集和每个数据点的连续潜在变量的情况,我们提出了AutoEncoding VB(AEVB)算法。在AEVB算法中,我们通过使用SGVB估计器来优化一个识别模型,使我们能够使用简单的祖先采样进行非常有效的近似后验推理,这反过来又使我们能够有效地学习模型参数,而无需每个数据点的昂贵迭代推理方案(如MCMC)。学习的近似后验推理模型也可以用于许多任务,如识别、去噪、表示和可视化目的。当神经网络用于识别模型时,我们得到了变分自编码器。
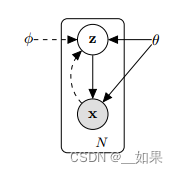
假设z满足一个分布p,由参数θ来描述;x是一个条件概率,是从z中抽样产生一个x
也就是z + θ抽样出x,x + Φ尝试推断出z
Method
The strategy in this section can be used to derive a lower bound estimator (a stochastic objective function) for a variety of directed graphical models with continuous latent variables. We will restrict ourselves here to the common case where we have an i.i.d. dataset with latent variables per datapoint, and where we like to perform maximum likelihood (ML) or maximum a posteriori (MAP) inference on the (global) parameters, and variational inference on the latent variables. It is, for example,straightforward to extend this scenario to the case where we also perform variational inference on the global parameters; that algorithm is put in the appendix, but experiments with that case are left to future work. Note that our method can be applied to online, non-stationary settings, e.g. streaming data, but here we assume a fixed dataset for simplicity.
翻译:
本节中的策略可以用来为具有连续潜在变量的各种有向图形模型导出一个下界估计器(一个随机目标函数)。在这里,我们将自己限制在一个常见的情况下,即我们有一个具有每个数据点的潜在变量的独立同分布数据集,并且我们希望对(全局)参数进行最大似然(ML)或最大后验概率(MAP)推理,对潜在变量进行变分推理。例如,将这个场景扩展到我们也对全局参数进行变分推理的情况是直接的;该算法放在附录中,但对这种情况的实验留待将来进行。请注意,我们的方法可以应用于在线、非平稳设置,例如流数据,但为了简单起见,这里我们假设一个固定数据集。
Problem scenario
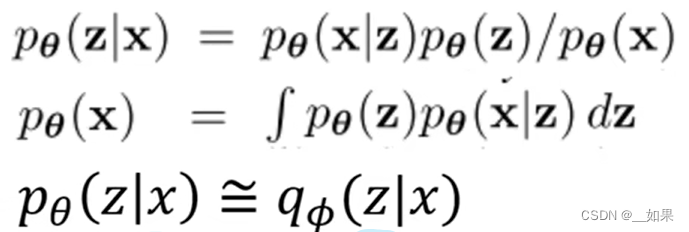
我们想得到的是给定x的情况下学得一个具有代表性的分布z,因此利用贝叶斯公式展开
其中x的分布是对这样一个式子的积分,但实际上x与z都是高维的,严格来写积分形式的话可能要写很多层积分号,这对我们来说是Intractable难解决的,从而无法得到given x的z
能不能用神经网络近似pθ(z|x)?我们使用另一个model,它的参数由Φ表示,得到了一个分布q,我们希望这个分布q能与p尽可能的接近
The variational bound
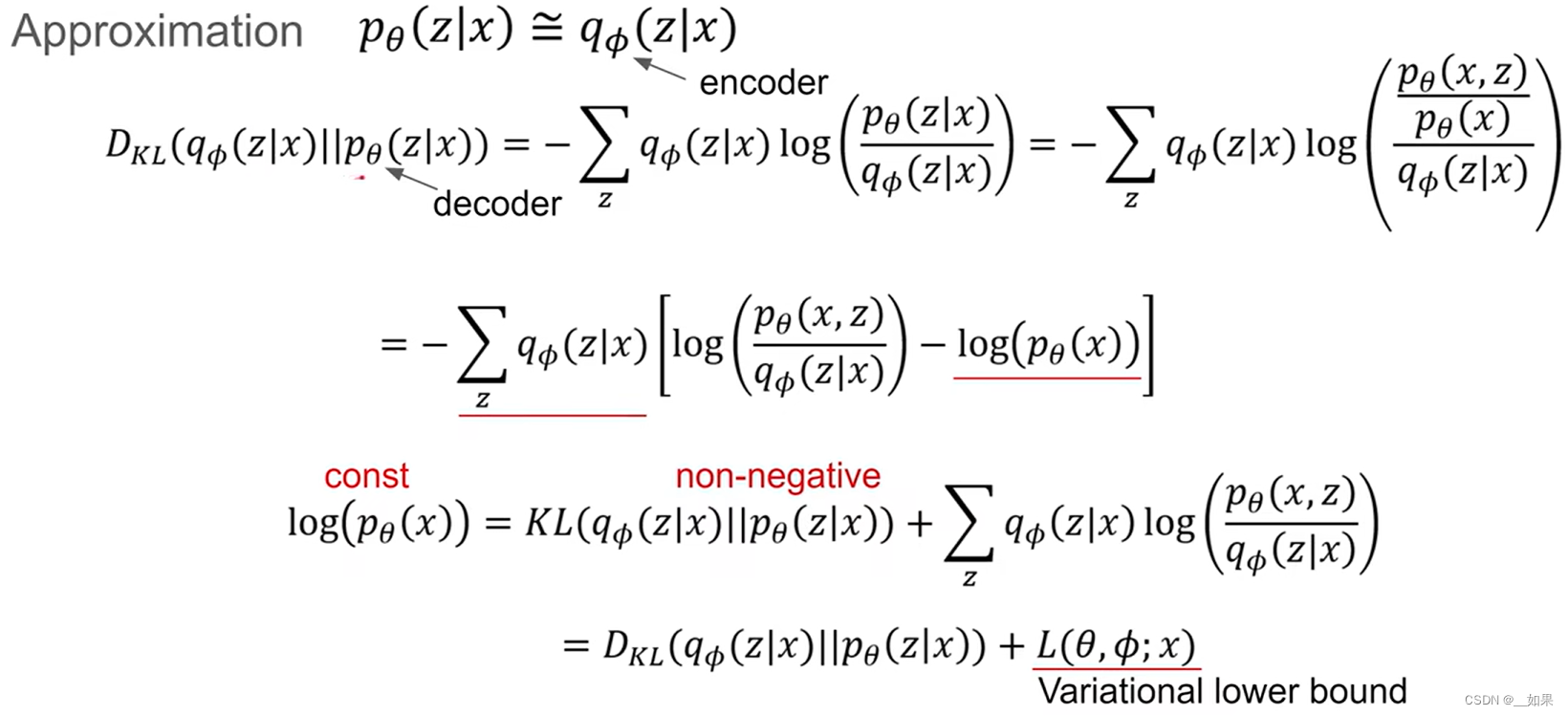
分布相近,那必然是用KL散度去衡量
对∑z来说,log(pθ(x))是无关的,而对qΦ(z|x)求和=1,所以提出来是常数放右边,而KL散度是非负的,因此最大化右边的式子(记作L(θ,Φ;x))就可以最小化KL散度,也就代表L(θ,Φ;x)是log(pθ(x))的下界

前面是given z后得到的x确实等于输入的x的概率的期望(reconstruction loss重建误差)
后面是希望qΦ分布跟先验分布z尽量接近(regularization loss正则误差)
第二行的式子可以写成期望的形式,也就代表着我们可以用蒙特卡洛法估计,把[ ]中的式子视作FC,同时假设Φ与FC是无关的

对FC在qΦ上的期望求梯度得到第一行中间的式子,然后通过采样求平均当作它的期望
to be more specific:是求梯度的推导,其中已经假设了Φ是无关的,所以可以直接放到f(x)之后
但是根据作者实验和前人报道,这样的estimator并不好,会有很高的方差,导致训练不稳定
The SGVB estimator and AEVB algorithm
&& The reparameterization trick

刚才我们用了一个很强的假设:Φ与FC无关,但其实是有关的,因此在推导梯度时不能直接放f(x)也就是fθ(z)的后面,而是应该分别求导,得到的后面一项是之前熟悉的期望形式,那么前一项呢?
为了解决前一项,作者引入了reparameterization trick(重参数化):引入一个辅助的随机变量ε,这个随机变量与θ、Φ、x、z都没关系,是独立的。用它来表达我们在产生z过程中所有的随机性,一次可以把z写成gθ(ε,x)
ε有个非常好的特性:它与θ,也就是Φ,是没有任何关系的,之后还是采样求平均得到期望
这样就可以把损失函数的梯度估计出来了
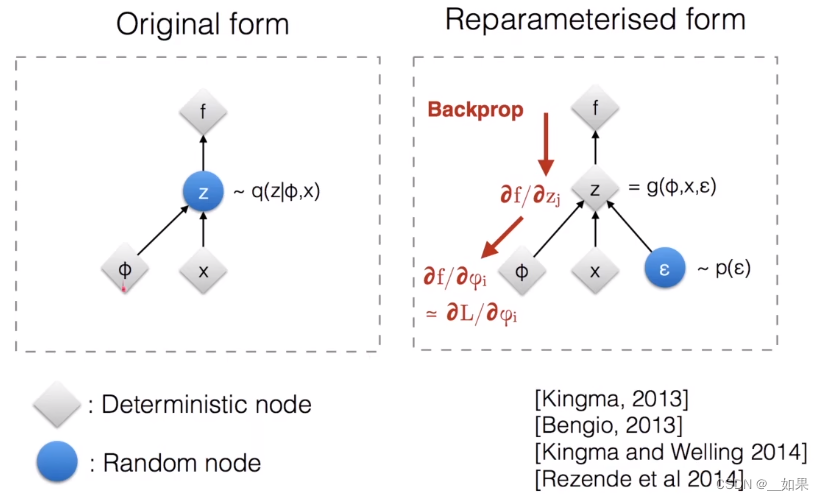
在原来的形式中,我们使用Φ和x产生distribution,然后从这个分布中抽样出一个z,得到f;抽样是没办法传递梯度的
在使用reparameterised trick之后,所有抽样中的随机性全在ε上,所以梯度就可以回传了

回到当初的分岔口,如果我们不用第二行的期望形式,而是第三行的期望+KL散度,我们发现KL散度也有一些很好的性质
假设qΦ与pθ都属于高斯分布,其中一项最后化简可以化为均值和方差的形式,另一项则化为:
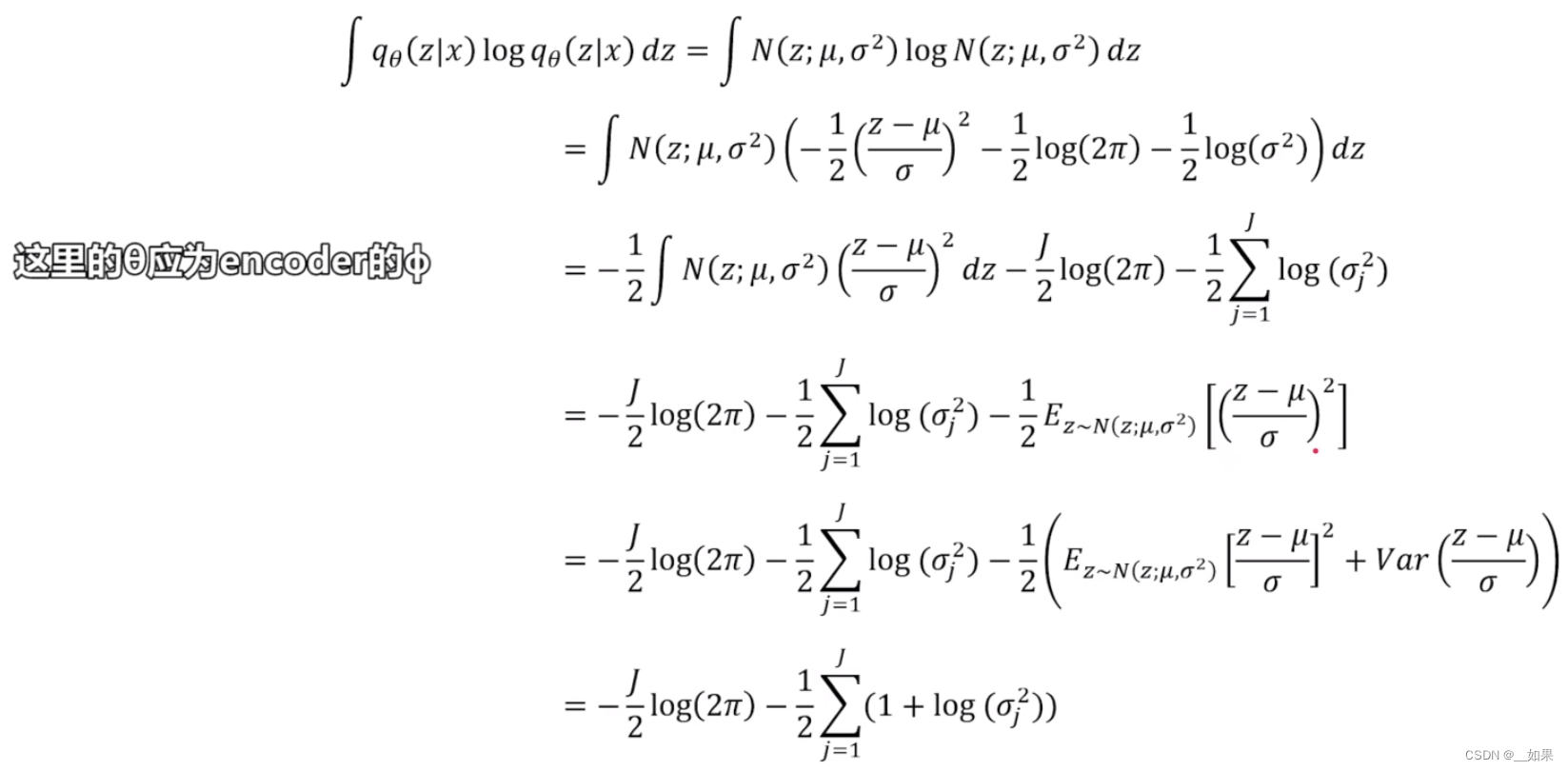
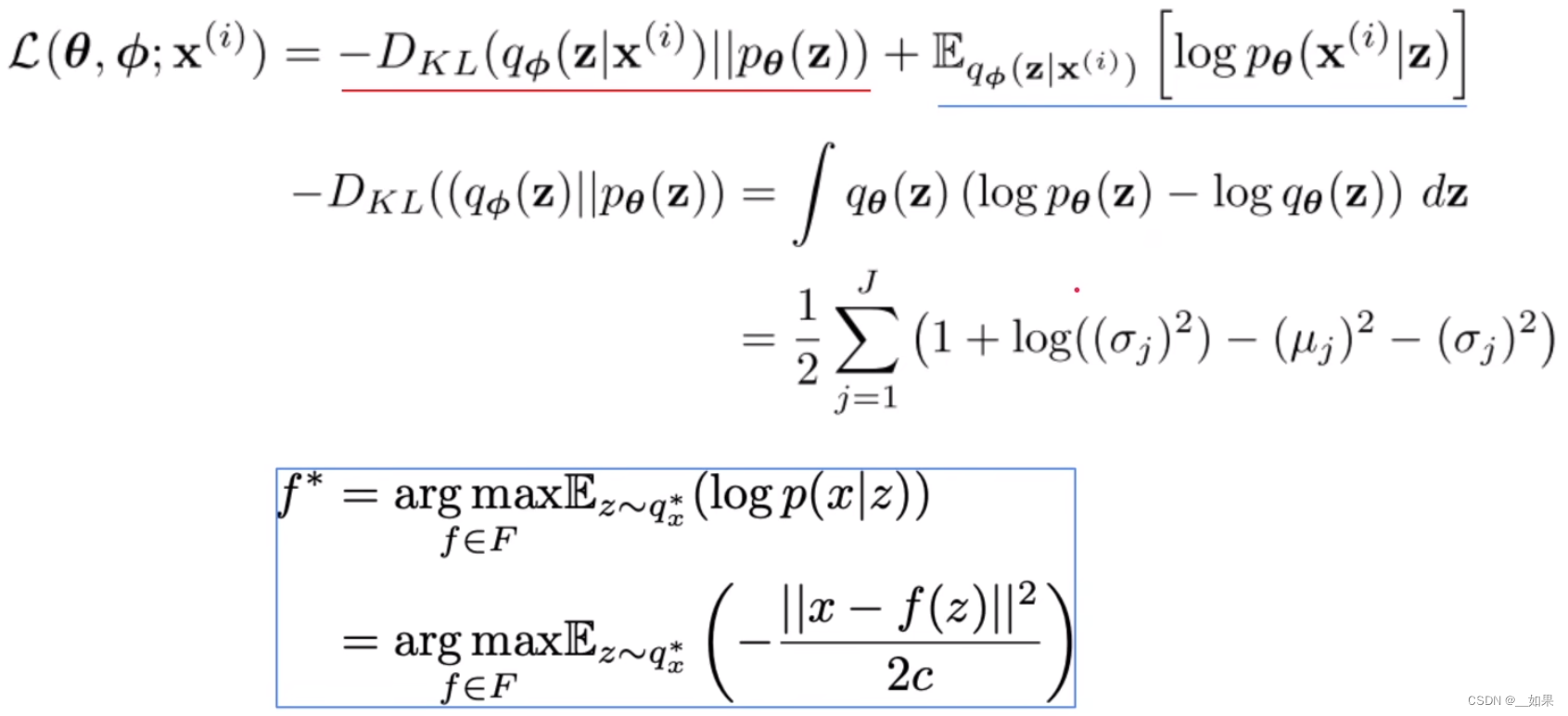 两项合并得到由均值和方差表示的KL散度,对后一项的期望直接求MSE算输入x与z生成的x的差异
两项合并得到由均值和方差表示的KL散度,对后一项的期望直接求MSE算输入x与z生成的x的差异
The Whole model architecture
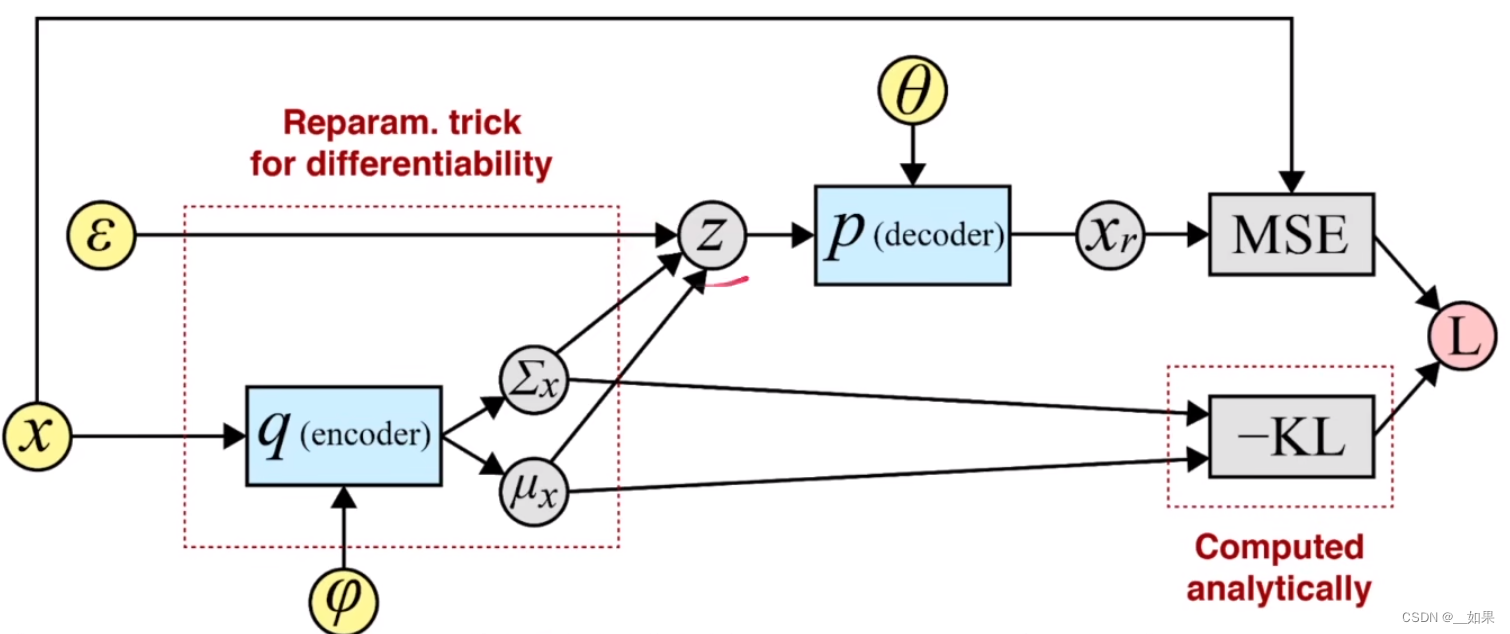
Experiments
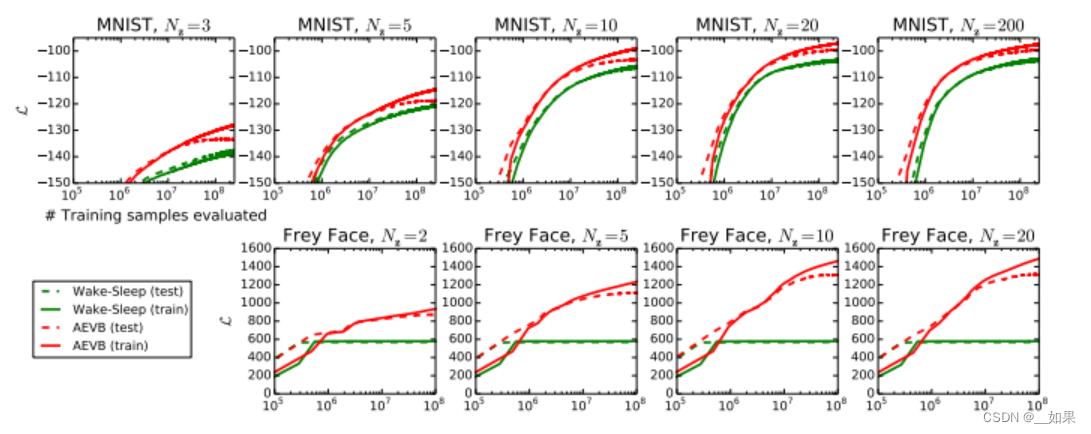
比较lower bound的提升,VAE收敛更快,lower bound更大,且更多的潜在变量并不会导致更多的过拟合,这可以通过lower bound的正则化效应来解释

更改方法)



)



 Groovy之HelloWorld)


】Lambda Architecture – Realtime Data Processing 论文重点翻译)
)


开题答辩常规问题和如何回答(答辩指导))


