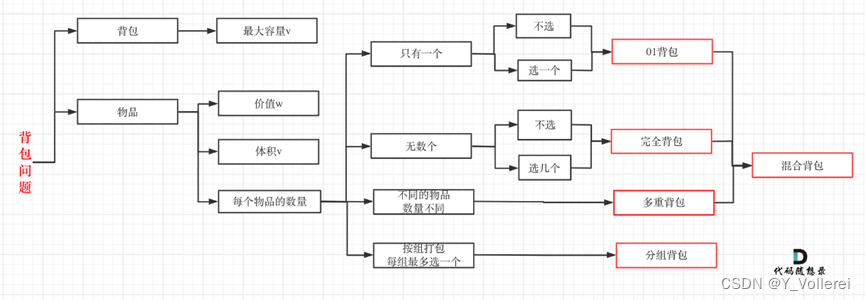
代码随想录算法训练营Day44 | 完全背包理论基础、518.零钱兑换 II、377.组合总和 Ⅳ

完全背包理论基础

完全背包看起来复杂不少，但其代码和0-1背包几乎没啥差别，就只改变了一个背包的遍历顺序：

基于0-1背包的滚动数组实现，将 j 的遍历顺序改为从左到右（此时物品会被重复使用）

完全背包的重点是如何使一个物品能够被重复使用。理解其实现前先回顾一下0-1背包是怎么让一个物品只使用一次的：

背包问题的递推公式：dp[j] = max(dp[j], dp[j - value[i]] + value[i])

这个递推公式中，每次更新使用dp[j]原先的值与其左边的值来更新dp[j]

如果 j 从右向左遍历，更新完dp[j]后继续向左遍历。对于每个dp[j]，只有一次与value[i]接触的机会。这就保证了每个物品只取一次。

如果将 j 的遍历顺序改为从左向右呢？dp[j]需要用到其左边的值（设其为dp[j - n]）来进行更新，此时需要取用一次物品 i ，而dp[i - n]也是由其左边的值更新来的，这里又可能会需要取用一次物品 i 。所以对于dp[i]来说就能够取用两次物品 i。随着逐渐向右遍历，dp[j]还可能使用更多次物品 i ，这就实现了物品 i 的复数次使用。

518.零钱兑换 II

这题理解了完全背包后还是比较简单的，没有脑筋急转弯，就是一道完全背包+组合的题，写法与昨天的494目标和差不多

int change(int amount, vector<int>& coins) {vector<int> dp(amount + 1, 0);dp[0] = 1;for (int i = 0; i < coins.size(); ++i) {// 完全背包在遍历滚动数组时，j的顺序是从左向右的for (int j = coins[i]; j <= amount; ++j) {dp[j] += dp[j - coins[i]];}}return dp[amount];
}

377.组合总和 Ⅳ

这题看题好像和上一题差不多，但再仔细看就能发现，这题是排列，而上一题是组合

看似复杂了不少，其实只要调换一下物品和背包的遍历嵌套关系就行：

· 对于组合问题，应该先遍历物品再遍历背包，这样物品是一类一类往背包里放的，物品i+1只能在物品i后放入背包
· 对于排列问题，应该先遍历背包再遍历物品，这样物品i+1能在物品i之前放入背包

（这题有一个恶心人的测试用例，所以在递推时需要多一步判断）

int combinationSum4(vector<int>& nums, int target) {vector<long> dp(target + 1, 0);dp[0] = 1;for (int j = 0; j <= target; ++j) {for (int i = 0; i < nums.size(); ++i) {if (nums[i] > j)continue;// 防止个别测试用例溢出if(dp[j] < INT_MAX - dp[j - nums[i]])dp[j] += dp[j - nums[i]];	}}return dp[target];
}