斯塔1和2是权重项，斯塔0是偏置项，在训练过程中为了使得训练结果更加精确而做的微调，不是一个大范围的因素，核心影响因素是权重项

为了完成矩阵的运算，在斯塔0后面乘x0，使得满足矩阵的转换，所以在处理数据时候会添加如有上图所示的x0一列全是1的数据

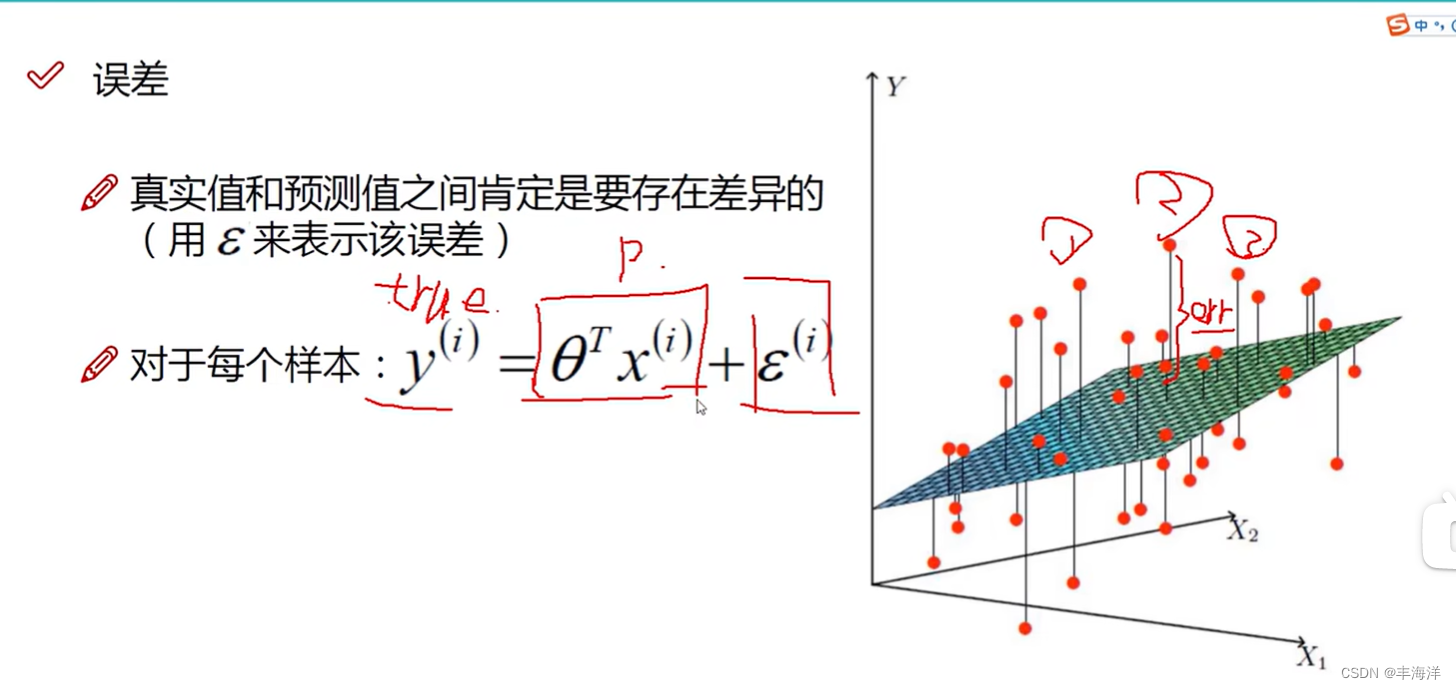
为了得出这个平面，我们要做的就是找出所有的未知量斯塔

• y为真实值，斯塔乘x是预测值，伊普西隆是误差值，每个样本的真实值和误差值都存在误差
• 什么是机器学习呢：就是你给机器一堆数据，机器通过数据不断学习，调整参数，最终得出完美符合数据特征的参数，机器学习==调参侠
• 我们要想求斯塔，就要将关于伊普西隆的算式转化成关于斯塔的算式

上图第三个算式左边的解释：x与斯塔组合后与y的数值越相近越好

所以p值越大越好

为什么是累乘？因为需要大量的数据去完善最后的参数，使得参数更加准确，因为乘法难解，所以可以加上对数转换成加法，而且转换后虽然L的数值改变了，但是我们要求取的是斯塔为何值使得L最大，所以不改变最后的斯塔数值

要让似然函数数值最大化，由于前面的项是一个常数项，所以后面的项就要最小化

这里的x和斯塔不是一个数，而是一个矩阵

经过求偏导，得出斯塔，但是机器学习是一个通过不断学习的过程不断完善斯塔这个参数，但是上面求解决斯塔的过程并没有一个学习的过程

做切线，走一小步，然后继续做切线，继续一小步，直到走到最低点

有一个问题：计算斯塔1和斯塔0的时候是一起计算好还是分别单独计算好呢？答案是分别计算，因为参数具有独立性

第二个问题：如何找到当前最合适的方向，求偏导

解释一下这张图上的目标函数为什么多了个平方：是因为将数据的误差效果放大

这个公式就是对目标函数求偏导得出方向，因为梯度下降是沿这原来的反方向走，所以后面那个公式前面的符号改变成＋号，表示在原来的初始位置斯塔j的位置走那么长的距离

由于批量梯度下降和随机梯度下降各有各的毛病，所以一般采用小批量梯度下降法，每次更新选择一小部分数据来算，比较实用

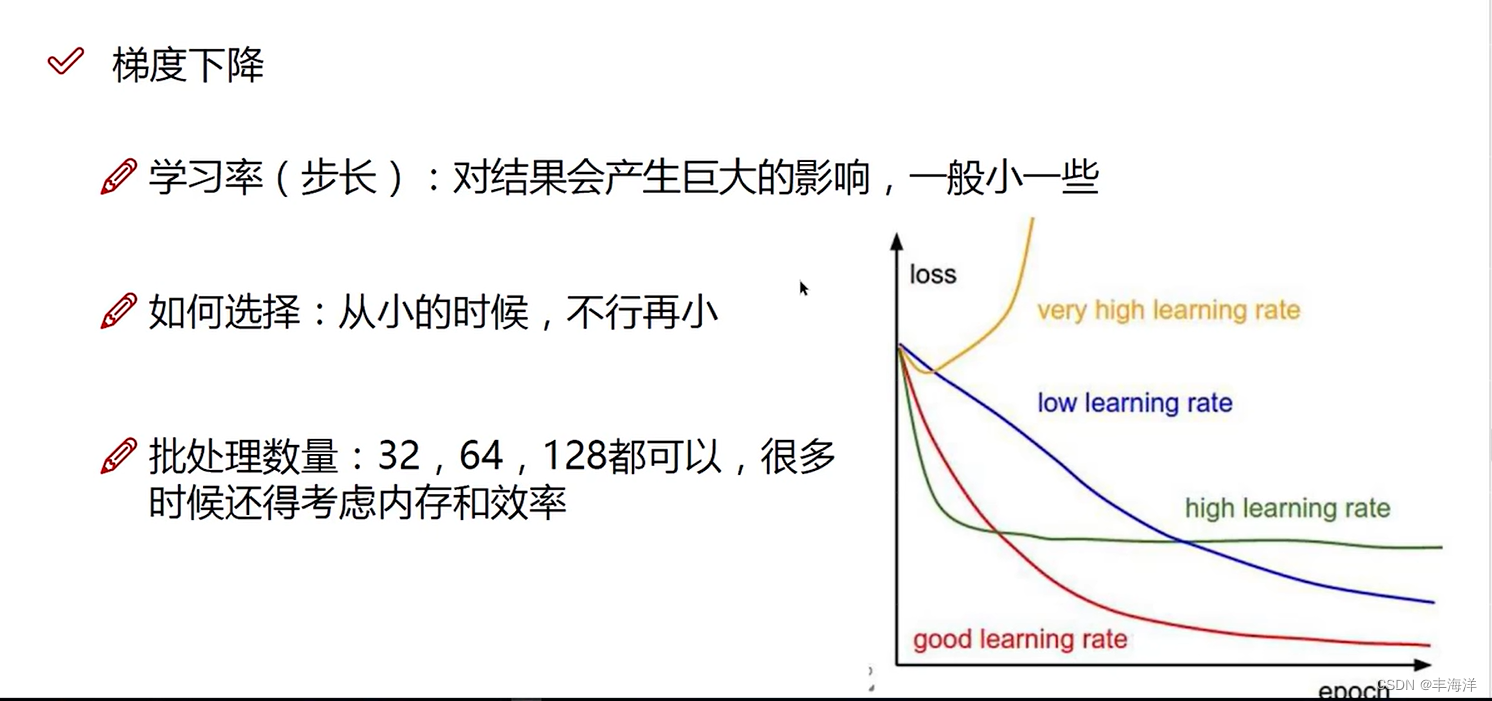
小批量梯度下降法公式中的α就是学习率，一般是0.01或者0.001

在写代码时，只需要完成上图花圈的部分就可以，m代表所有样本的个数，y代表真实值，h斯塔是预测值，xij也是样本中本来有的

import numpy as npdef prepare_for_training(data, polynomial_degree, sinusoid_degree, normalize_data):passclass LinearRegression:#polynomial_degree,sinusoid_degree,normalize_data目前来说没有用，当成摆设，data是数据，label是真实值ydef __init__(self,data,labels,polynomial_degree=0,sinusoid_degree=0,normalize_data=True):'''对数据进行预处理操作:data_processed表示处理后的数据，features_mean表示处理后数据的平均值，features_deviation表示处理后数据的方差'''(data_processed,features_mean,features_deviation)=prepare_for_training(data,polynomial_degree=0,sinusoid_degree=0,normalize_data=True)self.data=data_processedself.labels=labelsself.features_mean=features_meanself.features_deviation=features_deviationself.polynomial_degree=polynomial_degreeself.sinusoid_degree=sinusoid_degreeself.normalize_data=normalize_datanum_feature=self.data.shape[1]#得到data数据据中的列数，因为theta与data是一一对应的关系，故此将data中的列数取出来作为theta中的行数self.theta=np.zeros((num_feature,1))#初始化theta,num_feature行，1列的矩阵def train(self,alpha,num_iteration=500):#训练模型cost_history=self.gradient_descent(alpha,num_iteration)return self.theta,cost_historydef gradient_descent(self,alpha,num_iteration):#梯度下降cost_history=[]#存储损失值for _ in range(num_iteration):self.gradient_step(alpha)cost_history.append(self.cost_function(self.data,self.labels))#添加损失值return cost_historydef gradient_step(self,alpha):#公式实现&&参数的更新num_examples=self.data.shape[0]prediction=LinearRegression.hypothesis(self.data,self.theta)delta=prediction-self.labelstheta=self.thetatheta=theta-alpha*(1/num_examples)*(np.dot(delta.T,self.data)).Tself.theta=thetadef cost_function(self,data,labels):#损失函数，计算cost损失值num_examples=data.shape[0]delta=LinearRegression.hypothesis(self.data,self.theta)-labelscost=(1/2)*np.dot(delta.T,delta)/num_examplesreturn cost[0][0]@staticmethod#计算预测值def hypothesis(data,theta):predictions=np.dot(data,theta)return predictionsdef get_cost(self,data,labels):data_processed=prepare_for_training(data,self.polynomial_degree,self.sinusoid_degree,self.normalize_data)[0]return self.cost_function(data_processed,labels)def predict(self,data):data_processed=prepare_for_training(data,self.polynomial_degree,self.sinusoid_degree,self.normalize_data)[0]predictions=LinearRegression.hypothesis(data_processed,self.theta)return predictions