文章目录
- 计算图
- 符号微分
- 符号微分的步骤
- 示例
- 符号微分在计算图中的使用
- 总结
- 数值微分
- 前向差分法
- 中心差分法
- 数值微分的使用
- 注意事项
- 总结
- 自动微分
- 1. 基本原理
- 2. 主要类型
- 3. 计算图
- 4. 应用
- 5. 工具和库
- 6. 优点和缺点
- 计算图
- 1. **计算图的建立**
- 2. **前向传播**
- 3. **反向传播**
- 4. **链式法则和梯度计算**
- 5. **优点**
- 例子:
- 步骤1: 定义变量和运算
- 步骤2: 创建节点
- 步骤3: 创建边
- 步骤4: 执行前向传播
- 步骤5: (可选)执行反向传播
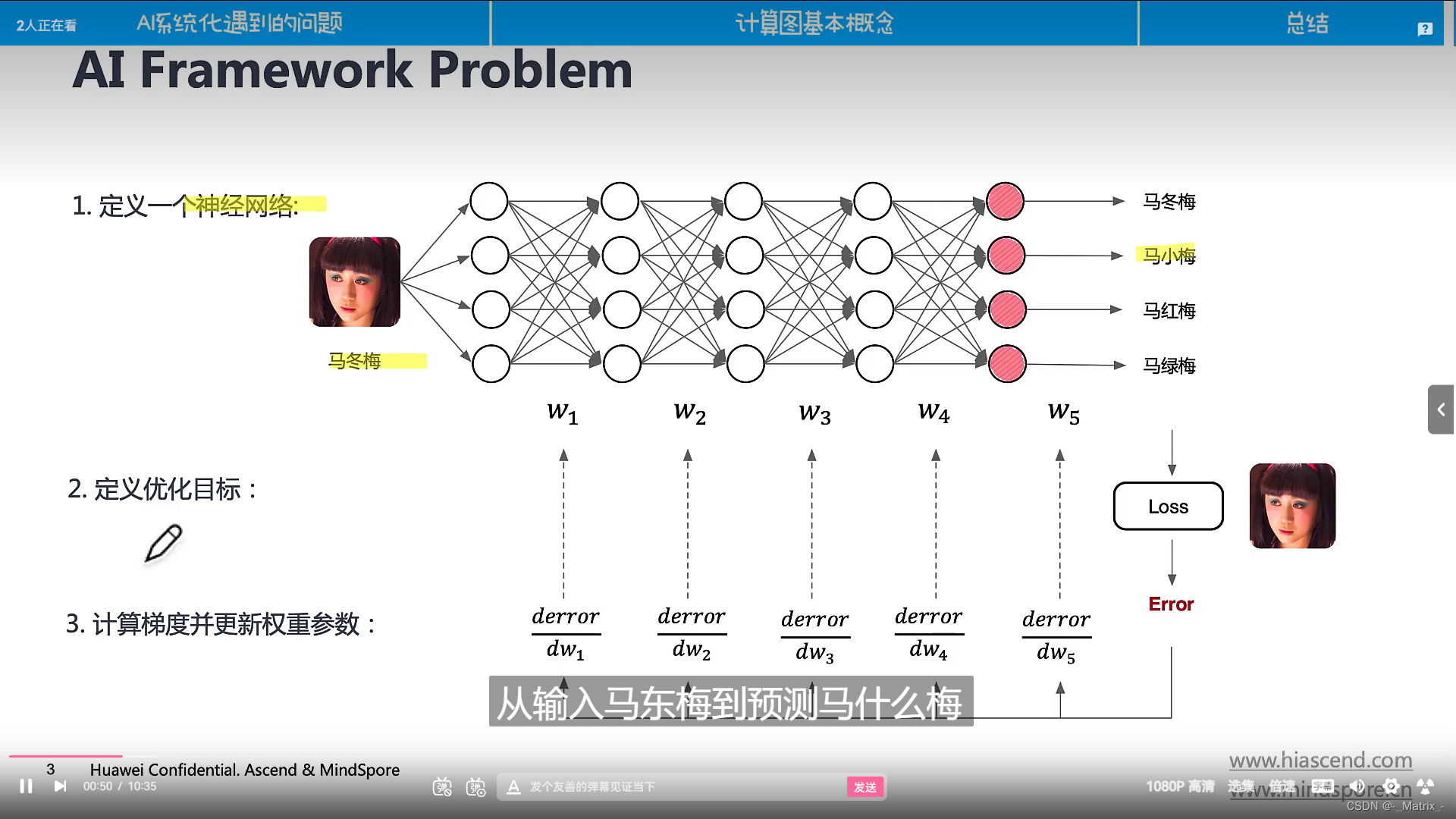
计算图

符号微分

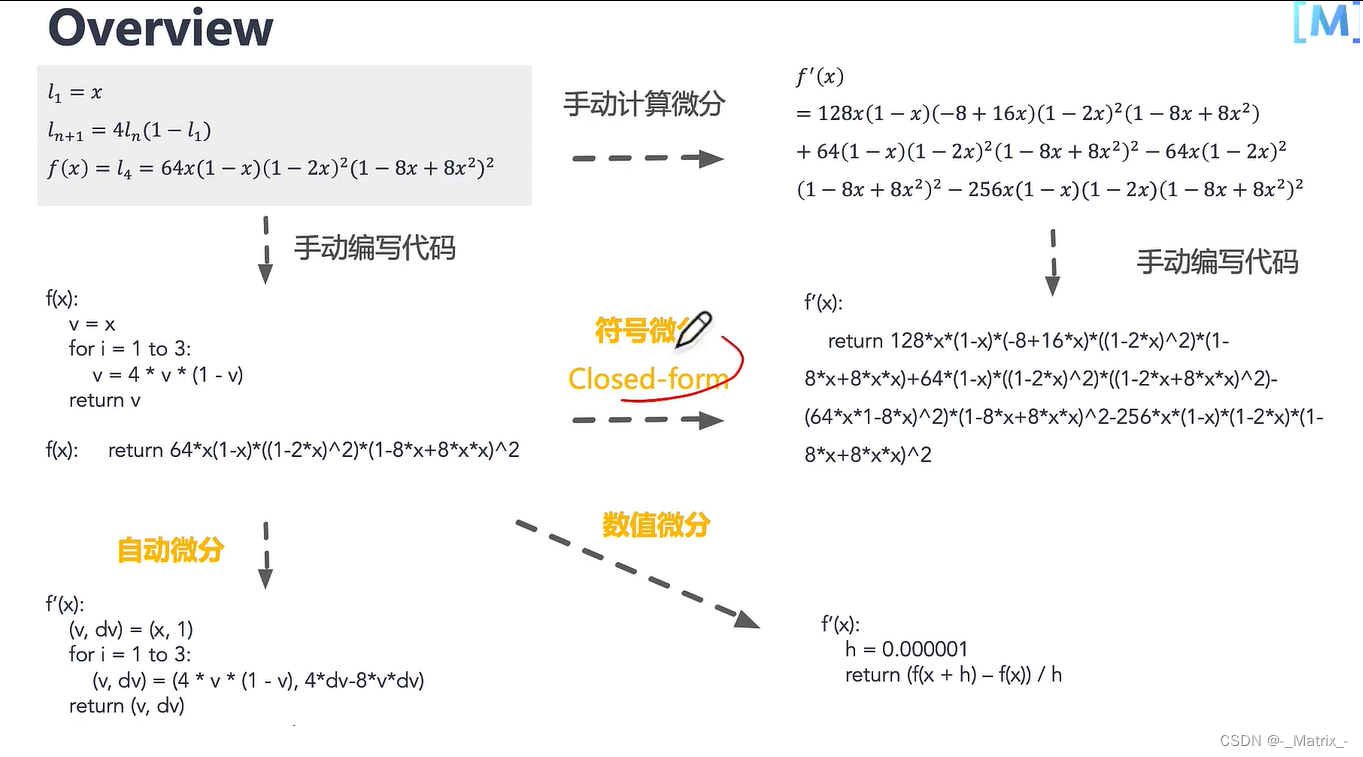
符号微分(Symbolic Differentiation)是一种使用数学表达式来表示微分或导数的技术。与数值微分不同,符号微分不是通过逼近来计算导数,而是直接处理数学表达式,得到一个精确的表达式,表示该函数的导数。
符号微分的步骤
-
表达式定义:首先,你需要一个表达式,例如一个多项式或任何可以微分的数学函数。
-
应用微分规则:然后,你会应用一系列微分规则(如乘积规则、商规则、链式法则等)来对表达式进行微分。
-
简化表达式:最后,你可能需要使用一些代数技巧来简化得到的导数表达式。
示例
假设你有一个函数 f ( x ) = x 2 + 3 x + 2 f(x) = x^2 + 3x + 2 f(x)=x2+3x+2,并且你想要找到其导数。通过符号微分,你可以应用基本的导数规则:
- d d x x n = n ⋅ x n − 1 \frac{d}{dx} x^n = n \cdot x^{n-1} dxdxn=n⋅xn−1
- d d x c = 0 \frac{d}{dx} c = 0 dxdc=0 (其中 c c c 是常数)
- 线性函数的导数等于其系数
这样,你可以找到 f ( x ) f(x) f(x)的导数:
f ′ ( x ) = 2 ⋅ x 1 + 3 ⋅ 1 + 0 = 2 x + 3 f'(x) = 2 \cdot x^1 + 3 \cdot 1 + 0 = 2x + 3 f′(x)=2⋅x1+3⋅1+0=2x+3
符号微分在计算图中的使用
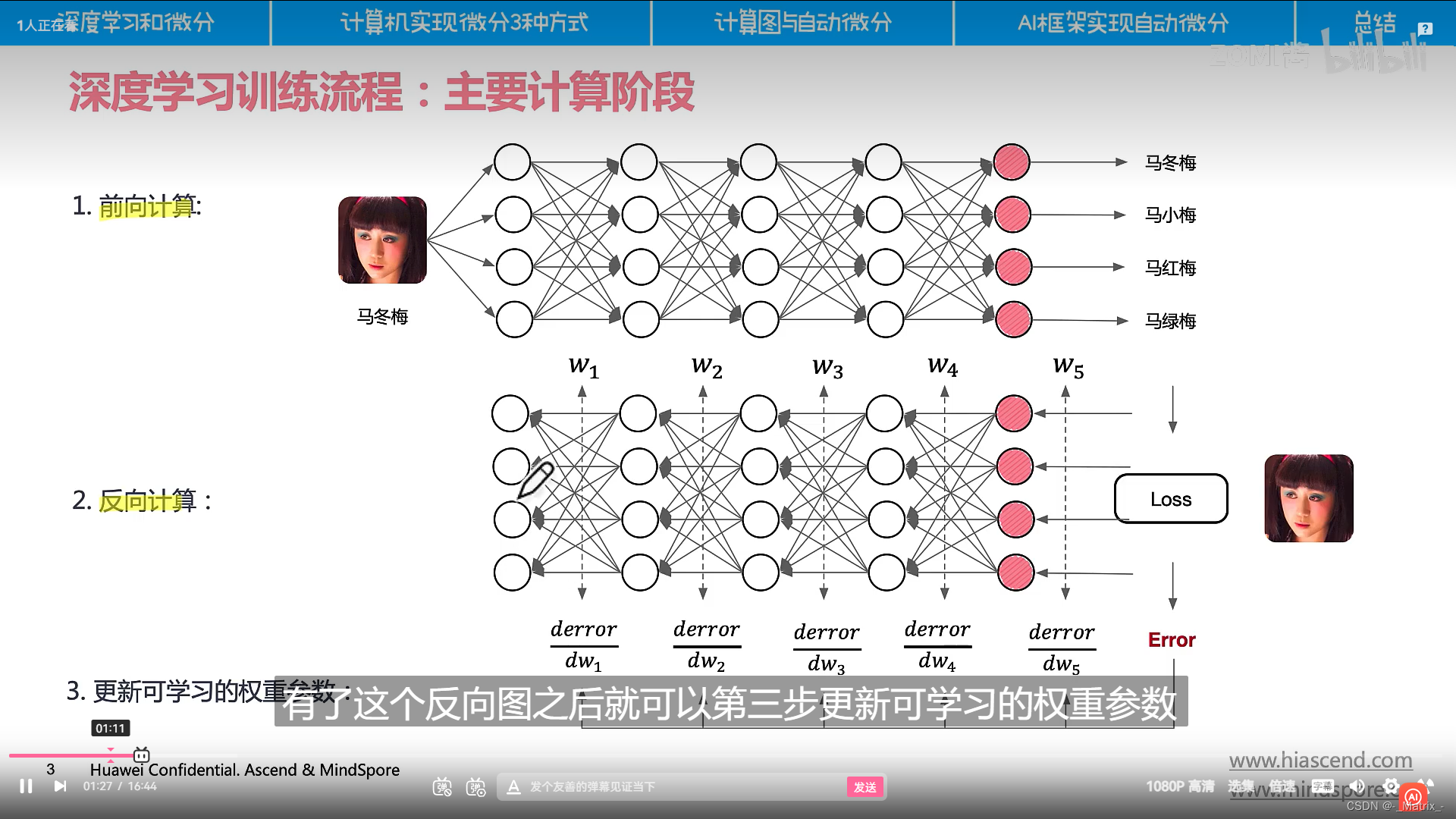
在深度学习中,符号微分经常与计算图结合使用:
- 前向传播:通过计算图表示模型的前向计算。
- 符号微分:应用符号微分来表示每个操作的局部导数。
- 反向传播:使用链式法则和计算图中的局部导数来计算整个模型的梯度。
这个过程允许深度学习框架自动计算模型的梯度,这是训练神经网络时所必需的。
总结
符号微分提供了一种精确、直接的方式来计算导数。在深度学习和其他科学计算应用中,通过结合计算图,符号微分使得自动求导和梯度下降优化变得可行和高效。不过,对于非常复杂的表达式,符号微分可能导致表达式膨胀,从而增加了计算复杂性。因此,有时可能会结合使用符号微分和数值微分方法。
数值微分

数值微分是一种近似计算函数导数的技术。与符号微分不同,数值微分不是通过解析地处理数学表达式来找到导数的精确形式,而是使用函数在特定点的数值来估计导数。
前向差分法
最简单的数值微分方法之一是前向差分法。假设你想要计算函数 f ( x ) f(x) f(x)在点 x x x处的导数,你可以使用以下公式:
f ′ ( x ) ≈ f ( x + h ) − f ( x ) h f'(x) \approx \frac{f(x + h) - f(x)}{h} f′(x)≈hf(x+h)−f(x)
其中 h h h是一个非常小的正数,称为步长。这个公式给出了在 x x x附近的函数的斜率的近似值。
中心差分法
前向差分方法的一个问题是,它可能不是非常精确,特别是当 h h h相对较大时。更精确的方法是中心差分法,使用以下公式:
f ′ ( x ) ≈ f ( x + h ) − f ( x − h ) 2 h f'(x) \approx \frac{f(x + h) - f(x - h)}{2h} f′(x)≈2hf(x+h)−f(x−h)
中心差分通过计算 f ( x ) f(x) f(x)在 x x x附近的两点的平均斜率,通常提供了更好的近似。
数值微分的使用
数值微分用于许多不同的应用领域,包括:
-
解析解不可用:当函数的导数很难或不可能解析地找到时,可以使用数值微分。
-
深度学习的梯度检查:在深度学习中,数值微分通常用于梯度检查,以确保使用符号微分(或自动微分)计算的梯度是正确的。
-
科学和工程应用:数值微分用于许多科学和工程应用,其中需要近似导数,但可能没有解析解。
注意事项
-
选择步长:选择合适的步长 h h h是一个关键问题。太大的步长可能会导致近似不精确,而太小的步长可能会导致数值不稳定。
-
数值不稳定:当涉及极小或极大的值时,数值微分可能会出现问题,因为计算机浮点数的精度有限。
-
计算成本:数值微分通常比符号微分更慢,因为它需要多次评估函数。
总结
数值微分是一种有用的工具,特别是当解析解不可用或难以获得时。它提供了一种灵活而实用的方法来近似导数,但必须谨慎选择参数并注意可能的数值问题。在深度学习和其他领域,它通常与符号微分或自动微分结合使用。
自动微分
视频链接:【前向微分和正向微分怎么理解?
自动微分(Automatic Differentiation,简称AD)是一种高效计算函数导数(或梯度)的技术。它不同于数值微分和符号微分,因为它可以提供更高的数值稳定性和计算效率。下面是自动微分的更多细节:
1. 基本原理
自动微分基于链式法则进行,它通过计算机程序来逐步计算和追踪函数的局部导数。基本的想法是将复杂函数分解为一系列简单的元素函数(例如加法、乘法等),并依次计算这些函数的导数。
2. 主要类型
自动微分可以分为两种主要类型:
- 前向模式(Forward Mode)
在前向模式中,我们从输入向量开始,然后通过每一个操作前进,计算每一步的局部导数和全局雅可比矩阵的相应部分。给定一个函数 f : R n → R m f: \mathbb{R}^n \rightarrow \mathbb{R}^m f:Rn→Rm,前向模式特别适合 n ≪ m n \ll m n≪m 的情况。
- 反向模式(Reverse Mode)
在反向模式中,我们首先进行一次正向传递来计算函数的输出,然后从输出向后进行一次传递来计算梯度或雅可比矩阵的每一部分。反向模式特别适合于 n ≫ m n \gg m n≫m 的情况,这也是为什么它被广泛应用于神经网络和深度学习,因为我们通常有许多输入和少量输出(例如损失函数)。
3. 计算图
自动微分常常依赖于一个计算图来表示和跟踪函数的计算过程。计算图是一种图形数据结构,其中每个节点代表一个操作,每个边代表数据流。
4. 应用
自动微分被广泛应用于各种领域,特别是在机器学习和优化问题中。它是训练神经网络时所用的反向传播算法的核心。
5. 工具和库
现有许多库和框架支持自动微分,如TensorFlow、PyTorch等,它们提供了方便的API来实现和使用自动微分技术。
6. 优点和缺点
- 优点:
- 高数值稳定性:比数值微分更稳定。
- 高效:特别是反向模式,它可以高效地计算梯度,尤其是对于有大量输入和少量输出的函数。
- 缺点:
- 内存消耗:反向模式可能需要大量的内存来存储中间结果。
- 实现复杂性:实现一个自动微分系统可能是非常复杂和技术性的。
计算图
自动微分通常是在计算图的基础上实现的。在计算图中,一个复杂函数被分解为多个简单的操作,这些操作被组织为一个有向图。现在,让我们更详细地了解自动微分和计算图之间的关系:
1. 计算图的建立
如我们前面所述,首先我们需要建立一个计算图,代表我们的函数。这涉及将函数分解为更简单的操作和变量,然后以有向图的形式表示这些操作和变量。
2. 前向传播
在计算图中,我们从输入变量开始,然后按照图中的顺序进行操作,直到我们计算出输出。这就是所谓的前向传播。
3. 反向传播
反向传播是自动微分的核心。在这一步,我们从输出开始,然后向后计算每一步的局部导数(或梯度)。这通常涉及应用链式法则,这是一种从输出向输入反向传播导数的方法。
4. 链式法则和梯度计算
通过使用链式法则,我们可以计算从输出到任何中间变量或输入的梯度。通过这种方式,我们可以得到我们想要的所有导数,而不是仅仅是输出相对于输入的导数。
5. 优点
- 精确度:自动微分可以提供与解析解几乎相同的精确度。
- 效率:它通常比数值微分方法更快、更稳定,尤其是对于具有许多变量的复杂函数。
例子:
使用给定的函数 f ( x , y ) = log ( x ) + x ⋅ y − sin ( y ) f(x, y) = \log(x) + x \cdot y - \sin(y) f(x,y)=log(x)+x⋅y−sin(y),我们可以构建一个计算图,将该函数分解为多个基本操作。下面是计算图的创建步骤:
步骤1: 定义变量和运算
首先,我们识别并定义所有的基本变量和运算:
- 变量: x x x, y y y
- 运算:
- log ( x ) \log(x) log(x)
- x ⋅ y x \cdot y x⋅y
- sin ( y ) \sin(y) sin(y)
- 加法和减法来组合上述结果
步骤2: 创建节点
然后,为每个变量和运算创建节点:
- 节点1(变量): x x x
- 节点2(变量): y y y
- 节点3(运算): log ( x ) \log(x) log(x)
- 节点4(运算): x ⋅ y x \cdot y x⋅y
- 节点5(运算): sin ( y ) \sin(y) sin(y)
- 节点6(运算): log ( x ) + x ⋅ y \log(x) + x \cdot y log(x)+x⋅y
- 节点7(运算): log ( x ) + x ⋅ y − sin ( y ) \log(x) + x \cdot y - \sin(y) log(x)+x⋅y−sin(y) (这是最终的输出节点)
步骤3: 创建边
接着,我们连接相应的边来形成有向图:
- 从节点1到节点3(表示 log ( x ) \log(x) log(x) 的输入是 x x x)
- 从节点1到节点4(表示 x ⋅ y x \cdot y x⋅y 的一个输入是 x x x)
- 从节点2到节点4(表示 x ⋅ y x \cdot y x⋅y 的另一个输入是 y y y)
- 从节点2到节点5(表示 sin ( y ) \sin(y) sin(y) 的输入是 y y y)
- 从节点3和节点4到节点6(表示他们的结果被加在一起)
- 从节点6和节点5到节点7(表示前者的结果减去后者的结果来得到最终输出)
步骤4: 执行前向传播
现在你可以执行前向传播来计算输出,按照操作的顺序一步步前进,直到达到输出节点。
步骤5: (可选)执行反向传播
如果你还打算进行自动微分,你可以实施反向传播算法来计算相对于 x x x 和 y y y 的偏导数。
代码实现:
///
/// \brief The Variable class
/// 自动微分
class Variable
{
public://保存值double value;//保存梯度double grad;//当前的梯度是否启用bool isEnableGrad;Variable(double v = 0.0,bool requires_grad=true,double g=0.0) : value(v), isEnableGrad(requires_grad),grad(g){}std::function<void()> backpropFunc;std::vector<std::shared_ptr<Variable>> parents;//设置求导函数void setBackprop(const std::function<void()>& func){backpropFunc = func;}//添加组成当前节点的节点void addParent(const std::shared_ptr<Variable>& parent){parents.push_back(parent);}//反向传播void backward(){if (backpropFunc)backpropFunc();for (auto& parent : parents){parent->backward();}}};//加法
inline std::shared_ptr<Variable> operator+(const std::shared_ptr<Variable>& a, const std::shared_ptr<Variable>& b)
{auto result = std::make_shared<Variable>(a->value + b->value);result->setBackprop([=]() {if(a->isEnableGrad)a->grad += result->grad;if (b->isEnableGrad)b->grad += result->grad;});result->addParent(a);result->addParent(b);return result;
}
//减法
inline std::shared_ptr<Variable> operator-(const std::shared_ptr<Variable>& a, const std::shared_ptr<Variable>& b)
{auto result = std::make_shared<Variable>(a->value - b->value);result->setBackprop([=]() {if (a->isEnableGrad)a->grad += result->grad;if (b->isEnableGrad)b->grad -= result->grad;});result->addParent(a);result->addParent(b);return result;
}//乘法
inline std::shared_ptr<Variable> operator*(const std::shared_ptr<Variable>& a, const std::shared_ptr<Variable>& b)
{auto result = std::make_shared<Variable>(a->value * b->value);result->setBackprop([=]() {if (a->isEnableGrad)a->grad += b->value * result->grad;if (b->isEnableGrad)b->grad += a->value * result->grad;});result->addParent(a);result->addParent(b);return result;
}
// 除法
inline std::shared_ptr<Variable> operator/(const std::shared_ptr<Variable>& a, const std::shared_ptr<Variable>& b)
{if (b->value == 0.0) {std::cerr << "Error: Division by zero!" << std::endl;exit(1);}auto result = std::make_shared<Variable>(a->value / b->value);result->setBackprop([=]() {if (a->isEnableGrad)a->grad += (1.0 / b->value) * result->grad;if (b->isEnableGrad)b->grad -= (a->value / (b->value * b->value)) * result->grad;});result->addParent(a);result->addParent(b);return result;
}
// sin
inline std::shared_ptr<Variable> sin(const std::shared_ptr<Variable>& a)
{auto result = std::make_shared<Variable>(std::sin(a->value));result->setBackprop([=]() {if (a->isEnableGrad)a->grad += std::cos(a->value) * result->grad;});result->addParent(a);return result;
}
// cos
inline std::shared_ptr<Variable> cos(const std::shared_ptr<Variable>& a)
{auto result = std::make_shared<Variable>(std::cos(a->value));result->setBackprop([=]() {if (a->isEnableGrad)a->grad -= std::sin(a->value) * result->grad; // 注意这里是减号,因为cos的导数是-sin});result->addParent(a);return result;
}// log
inline std::shared_ptr<Variable> log(const std::shared_ptr<Variable>& a)
{if (a->value <= 0.0) {std::cerr << "Error: Logarithm of non-positive number!" << std::endl;exit(1);}auto result = std::make_shared<Variable>(std::log(a->value));result->setBackprop([=]() {if (a->isEnableGrad)a->grad += (1.0 / a->value) * result->grad; // 导数为 1/x});result->addParent(a);return result;
}// exp
inline std::shared_ptr<Variable> exp(const std::shared_ptr<Variable>& a)
{auto result = std::make_shared<Variable>(std::exp(a->value));result->setBackprop([=]() {if (a->isEnableGrad)a->grad += std::exp(a->value) * result->grad; // 导数为 e^x});result->addParent(a);return result;
}int main() {auto x = std::make_shared<Variable>(2.0); // 创建一个初值为2的变量xauto y = std::make_shared<Variable>(5.0,false); // false 不计算y的梯度auto g = log(x) + x * y - sin(y);g->grad = 1.0; // df/df = 1g->backward();std::cout << "df/dx = " << x->grad << std::endl;std::cout << "df/dy = " << y->grad << std::endl;return 0;
}


-ControlNet(Inpaint))



)
——利用谷歌地球引擎中的交互式桑基图可视化分类时间序列数据的变化(2000-2020年不同土地转化可视化))



:PL/SQL编程)






![[c++] 单例模式 + cyberrt TimingWheel 单例分析](http://pic.xiahunao.cn/[c++] 单例模式 + cyberrt TimingWheel 单例分析)

)