606. 根据二叉树创建字符串
给你二叉树的根节点
root,请你采用前序遍历的方式,将二叉树转化为一个由括号和整数组成的字符串,返回构造出的字符串。空节点使用一对空括号对
"()"表示,转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。示例 1:
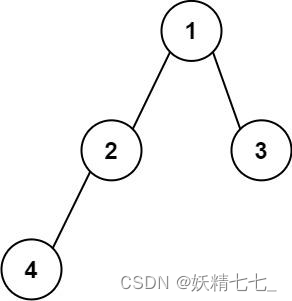
输入:root = [1,2,3,4] 输出:"1(2(4))(3)" 解释:初步转化后得到 "1(2(4)())(3()())" ,但省略所有不必要的空括号对后,字符串应该是"1(2(4))(3)" 。示例 2:
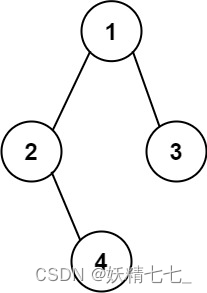
输入:root = [1,2,3,null,4] 输出:"1(2()(4))(3)" 解释:和第一个示例类似,但是无法省略第一个空括号对,否则会破坏输入与输出一一映射的关系。提示:
树中节点的数目范围是
[1, 10(4)]
-1000 <= Node.val <= 1000
class Solution {
public:string tree2str(TreeNode *root) {if (root == nullptr) {return "";}if (root->left == nullptr && root->right == nullptr) {return to_string(root->val);}if (root->right == nullptr) {return to_string(root->val) + "(" + tree2str(root->left) + ")";}return to_string(root->val) + "(" + tree2str(root->left) + ")(" + tree2str(root->right) + ")";}
};
这道题目蕴含的规则,
-
每个节点的值都转换成字符串。
-
对于非叶子节点,其左子节点(如果存在)的字符串表示将被放置在一对括号内紧跟在该节点的值之后。如果左子节点不存在但右子节点存在,将使用一对空括号
()表示左子节点的位置。 -
对于非叶子节点,其右子节点(如果存在)的字符串表示将被放置在一对括号内,紧跟在左子节点的字符串表示之后。
空节点:如果当前节点是nullptr,返回空字符串""。
叶子节点:如果当前节点是叶子节点(即没有左子节点也没有右子节点),仅返回当前节点值的字符串表示。
只有左子节点:如果当前节点仅有左子节点(没有右子节点),则返回当前节点值的字符串表示,后面跟着左子节点的字符串表示,左子节点的字符串表示被一对括号包围。
既有左子节点也有右子节点:如果当前节点既有左子节点也有右子节点,返回当前节点值的字符串表示,后面依次跟着左子节点和右子节点的字符串表示,这两个子节点的字符串表示各自被一对括号包围。

102. 二叉树的层序遍历
给你二叉树的根节点
root,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。示例 1:
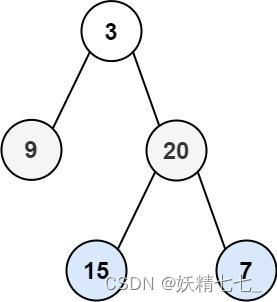
输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]示例 2:
输入:root = [1] 输出:[[1]]示例 3:
输入:root = [] 输出:[]提示:
树中节点数目在范围
[0, 2000]内
-1000 <= Node.val <= 1000
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector <vector <int>> ret;if (!root) {return ret;}queue <TreeNode*> q;q.push(root);while (!q.empty()) {int currentLevelSize = q.size();ret.push_back(vector <int> ());for (int i = 1; i <= currentLevelSize; ++i) {auto node = q.front(); q.pop();ret.back().push_back(node->val);if (node->left) q.push(node->left);if (node->right) q.push(node->right);}}return ret;}
};
如果传入的根节点root为空,则函数立即返回一个空的二维向量ret。
初始化一个队列q,用于存储待访问的节点。首先将根节点root入队。
当队列不为空时,进行循环。循环的每一轮对应树的一层。
在循环开始时,记录当前队列的大小currentLevelSize,这个大小代表了当前层的节点数。
添加一个新的空向量到ret中,用于存储当前层的节点值。
通过一个for循环遍历当前层的所有节点。循环次数由currentLevelSize决定。
每次循环中,从队列中取出队首元素(node),这代表当前层的一个节点。
将node的值加入到ret的最后一个向量中,这个向量代表当前层的节点值集合。
如果node的左子节点存在,则将左子节点入队;如果node的右子节点存在,则将右子节点入队。这确保了下一层的节点将会在后续的迭代中被处理。

107. 二叉树的层序遍历 II
给你二叉树的根节点
root,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)示例 1:
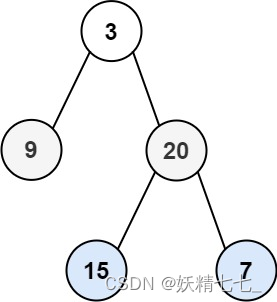
输入:root = [3,9,20,null,null,15,7] 输出:[[15,7],[9,20],[3]]示例 2:
输入:root = [1] 输出:[[1]]示例 3:
输入:root = [] 输出:[]提示:
树中节点数目在范围
[0, 2000]内
-1000 <= Node.val <= 1000
class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {vector<vector<int>> ret;if (!root) {return ret;}queue<TreeNode*> q;q.push(root);while (!q.empty()) {int currentLevelSize = q.size();ret.push_back(vector<int>());for (int i = 1; i <= currentLevelSize; i++) {auto node = q.front();q.pop();ret.back().push_back(node->val);if (node->left)q.push(node->left);if (node->right)q.push(node->right);}}reverse(ret.begin(), ret.end());return ret;}
};如果传入的根节点root为空,则函数立即返回一个空的二维向量ret。
初始化一个队列q,用于存储待访问的节点。首先将根节点root入队。
当队列不为空时,进行循环。循环的每一轮对应树的一层。
在循环开始时,记录当前队列的大小currentLevelSize,这个大小代表了当前层的节点数。
添加一个新的空向量到ret中,用于存储当前层的节点值。
通过一个for循环遍历当前层的所有节点。循环次数由currentLevelSize决定。
每次循环中,从队列中取出队首元素(node),这代表当前层的一个节点。
将node的值加入到ret的最后一个向量中,这个向量代表当前层的节点值集合。
如果node的左子节点存在,则将左子节点入队;如果node的右子节点存在,则将右子节点入队。这确保了下一层的节点将会在后续的迭代中被处理。
在完成所有层的遍历后,使用reverse函数将ret中的向量顺序反转,以达到自底向上的层序遍历效果。
236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
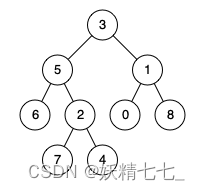
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出:3 解释:节点 5 和节点 1 的最近公共祖先是节点 3 。示例 2:
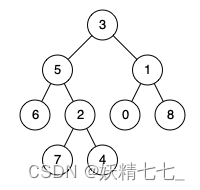
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出:5 解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。示例 3:
输入:root = [1,2], p = 1, q = 2 输出:1提示:
树中节点数目在范围
[2, 10(5)]内。
-10(9) <= Node.val <= 10(9)所有
Node.val互不相同。
p != q
p和q均存在于给定的二叉树中。
class Solution {
public:TreeNode* ans;bool dfs(TreeNode* root, TreeNode* p, TreeNode* q) {if (root == nullptr)return false;bool lson = dfs(root->left, p, q);bool rson = dfs(root->right, p, q);if ((lson && rson) ||((root->val == p->val || root->val == q->val) && (lson || rson))) {ans = root;}return lson || rson || (root->val == p->val || root->val == q->val);}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {dfs(root, p, q);return ans;}
};
dfs 函数:
遍历树以检查当前节点root是否是p或q的祖先,或者是否自身是p或q。
当前考察的节点root,以及要找的节点p和q。
如果当前root或其任何子节点是p或q,则返回true,否则返回false。
逻辑:
如果当前节点是nullptr,返回false。
检查当前节点的左子树(lson)和右子树(rson)是否包含p或q。
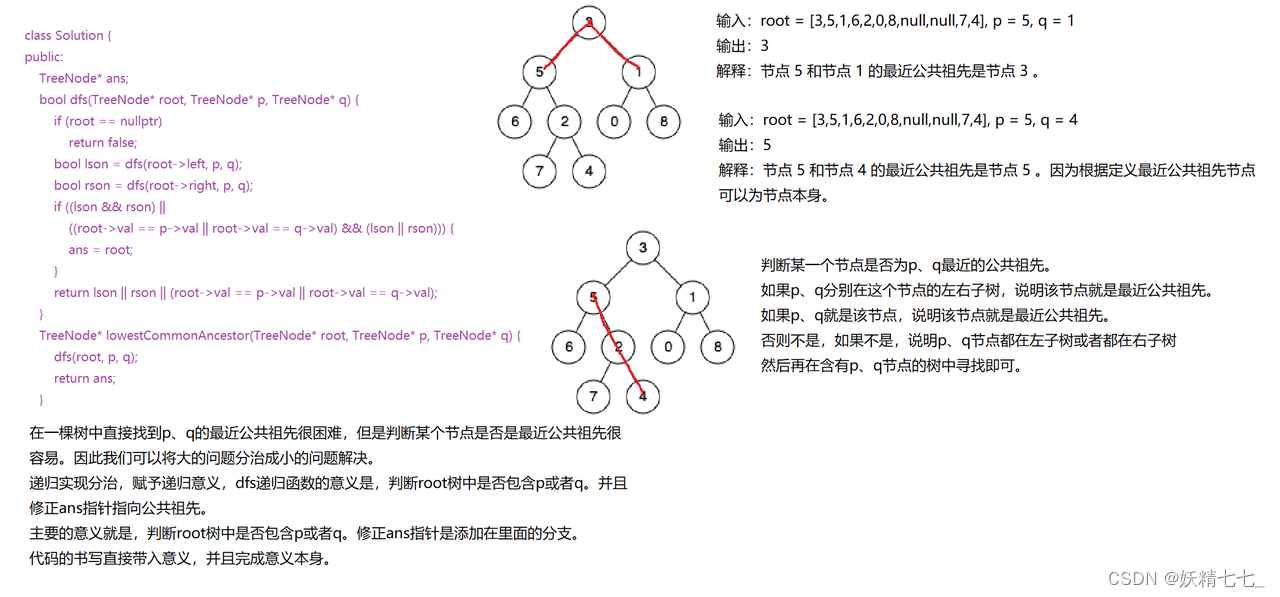
如果下面任一条件为真,则当前节点root是p和q的最低公共祖先:
lson和rson都为真,意味着p和q分别位于当前节点的两侧。
当前节点是p或q之一,并且p或q中的另一个位于当前节点的某个子树中。
更新ans为当前的最低公共祖先节点。
lowestCommonAncestor 函数:
找到并返回给定二叉树中两个节点p和q的最低公共祖先。
调用dfs函数遍历树,dfs过程中会更新ans为p和q的最低公共祖先。完成遍历后,ans即为所求的最低公共祖先节点。
二叉搜索树与双向链表_牛客题霸_牛客网
描述
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。如下图所示
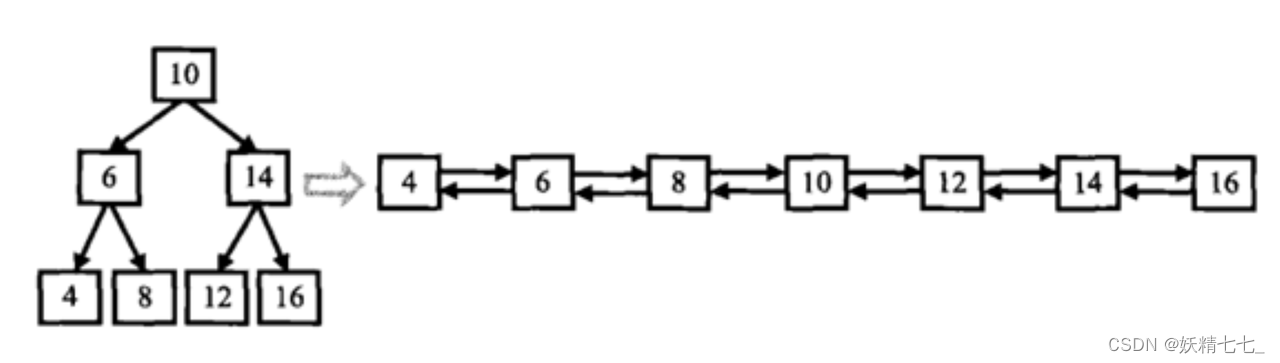
数据范围:输入二叉树的节点数 0≤n≤1000,二叉树中每个节点的值 0≤val≤1000 要求:空间复杂度O(1)(即在原树上操作),时间复杂度O(n)
注意:
1.要求不能创建任何新的结点,只能调整树中结点指针的指向。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继 2.返回链表中的第一个节点的指针 3.函数返回的TreeNode,有左右指针,其实可以看成一个双向链表的数据结构
4.你不用输出双向链表,程序会根据你的返回值自动打印输出
输入描述:
二叉树的根节点
返回值描述:
双向链表的其中一个头节点。
示例1
输入:
{10,6,14,4,8,12,16}返回值:
From left to right are:4,6,8,10,12,14,16;From right to left are:16,14,12,10,8,6,4;说明:
输入题面图中二叉树,输出的时候将双向链表的头节点返回即可。
示例2
输入:
{5,4,#,3,#,2,#,1}返回值:
From left to right are:1,2,3,4,5;From right to left are:5,4,3,2,1;说明:
5 / 4 / 3 / 2 / 1 树的形状如上图
法一:中序+链接
/*
struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;TreeNode(int x) :val(x), left(NULL), right(NULL) {}
};*/
class Solution {
public:vector<TreeNode*> TreeList;//定义一个数组,根据中序遍历来存储结点。void inorder(TreeNode* root){if (!root) return;inorder(root->left);TreeList.push_back(root);inorder(root->right);}TreeNode* Convert(TreeNode* pRootOfTree) {if (!pRootOfTree) return pRootOfTree;inorder(pRootOfTree);for (int i=0;i<TreeList.size()-1;i++){ //根据数组中的顺序将结点连接,注意i的范围。TreeList[i]->right = TreeList[i+1];TreeList[i+1]->left = TreeList[i];}return TreeList[0];//数组的头部存储的是双向链表的第一个结点。}};中序遍历 (inorder 函数)
inorder 函数对二叉树进行中序遍历。中序遍历的顺序是先遍历左子树,然后访问根节点,最后遍历右子树。
在遍历过程中,每访问到一个节点,就将其加入到TreeList向量中。由于是中序遍历,TreeList中的节点自然按照值的升序排列。
转换为双向链表 (Convert 函数)
Convert 函数首先检查给定的树(pRootOfTree)是否为空。如果为空,则直接返回空指针。
然后,调用inorder函数进行中序遍历,填充TreeList向量。
接下来,遍历TreeList向量,将每个节点按顺序连接起来形成双向链表。对于向量中的每个节点,除了最后一个节点外:
将当前节点的right指针指向下一个节点。
将下一个节点的left指针指向当前节点。
最后,返回TreeList中的第一个元素,即双向链表的头节点。
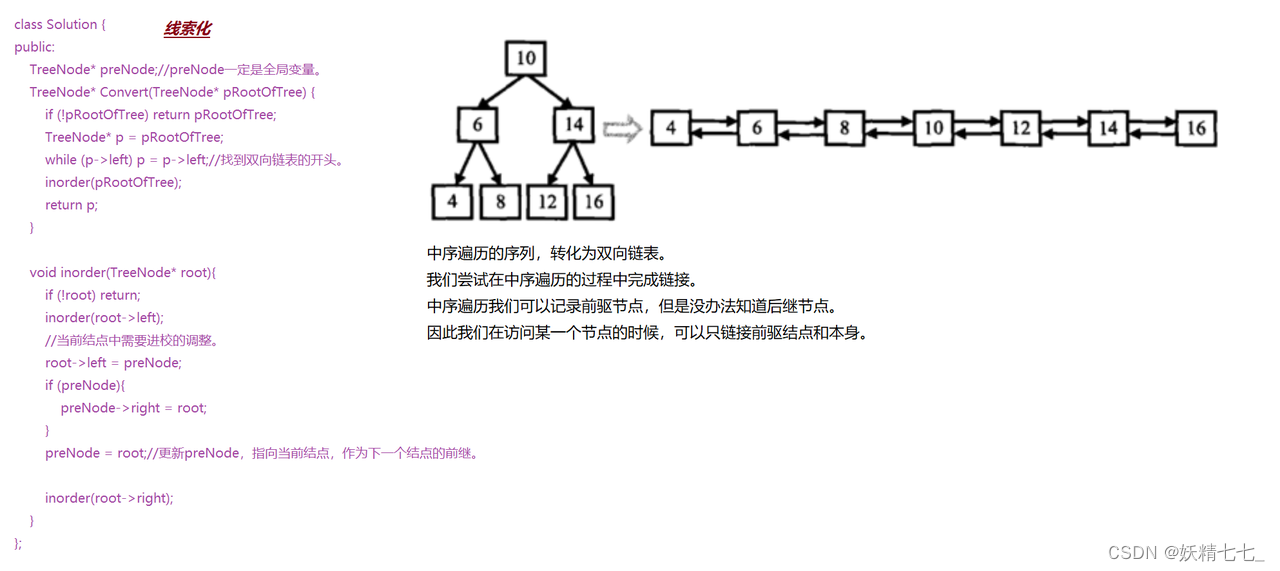
法二:线索化
/*
struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;TreeNode(int x) :val(x), left(NULL), right(NULL) {}
};*/
class Solution {
public:TreeNode* preNode;//preNode一定是全局变量。TreeNode* Convert(TreeNode* pRootOfTree) {if (!pRootOfTree) return pRootOfTree;TreeNode* p = pRootOfTree;while (p->left) p = p->left;//找到双向链表的开头。inorder(pRootOfTree);return p;}void inorder(TreeNode* root){if (!root) return;inorder(root->left);//当前结点中需要进校的调整。root->left = preNode;if (preNode){preNode->right = root;}preNode = root;//更新preNode,指向当前结点,作为下一个结点的前继。inorder(root->right);}
};Convert 函数:
首先检查树是否为空。如果是空树,则直接返回空指针。
然后找到最左边的节点,这将是双向链表的头节点。这一步确保能返回转换后的双向链表的起始点。
调用inorder函数进行中序遍历并在遍历过程中逐步构造双向链表。
inorder 函数:
这个函数通过中序遍历递归地访问树的每个节点。
在访问每个节点时,它将当前节点的left指针指向preNode(即中序遍历中当前节点的前一个节点)。
如果preNode非空,它还将preNode的right指针指向当前节点,从而在两个节点之间建立双向连接。
然后更新preNode为当前节点,以便在下一次迭代中使用。
105. 从前序与中序遍历序列构造二叉树
给定两个整数数组
preorder和inorder,其中preorder是二叉树的先序遍历,inorder是同一棵树的中序遍历,请构造二叉树并返回其根节点。示例 1:
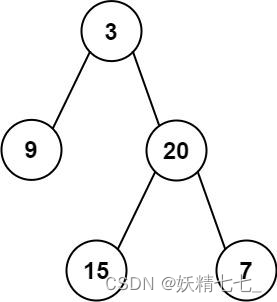
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1] 输出: [-1]
提示:
1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder和inorder均 无重复 元素
inorder均出现在preorder
preorder保证 为二叉树的前序遍历序列
inorder保证 为二叉树的中序遍历序列
class Solution {
private:unordered_map<int, int> index;public:TreeNode* myBuildTree(const vector<int>& preorder,const vector<int>& inorder, int preorder_left,int preorder_right, int inorder_left,int inorder_right) {if (preorder_left > preorder_right) {return nullptr;}// 前序遍历中的第一个节点就是根节点int preorder_root = preorder_left;// 在中序遍历中定位根节点int inorder_root = index[preorder[preorder_root]];// 先把根节点建立出来TreeNode* root = new TreeNode(preorder[preorder_root]);// 得到左子树中的节点数目int size_left_subtree = inorder_root - inorder_left;// 递归地构造左子树,并连接到根节点// 先序遍历中「从 左边界+1 开始的// size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到// 根节点定位-1」的元素root->left = myBuildTree(preorder, inorder, preorder_left + 1,preorder_left + size_left_subtree,inorder_left, inorder_root - 1);// 递归地构造右子树,并连接到根节点// 先序遍历中「从 左边界+1+左子树节点数目 开始到// 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素root->right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1,preorder_right, inorder_root + 1, inorder_right);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int n = preorder.size();// 构造哈希映射,帮助我们快速定位根节点for (int i = 0; i < n; ++i) {index[inorder[i]] = i;}return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);}
};
buildTree 函数:
这个函数是公有的,作为类外部调用的接口。它接受两个参数:分别代表二叉树前序遍历和中序遍历的数组。
首先,函数通过遍历中序遍历数组来填充一个哈希映射index,该映射用于快速查找中序遍历中任一值对应的索引,这样可以快速定位到根节点在中序遍历中的位置。
然后,调用私有的myBuildTree函数,传入前序遍历和中序遍历的数组及其对应的索引范围,开始递归构造树。
myBuildTree 函数:
这是一个递归函数,用于根据给定的前序遍历和中序遍历的一部分来构造子树,并返回子树的根节点。
首先,检查当前递归的子数组是否有效(即前序遍历的左索引是否大于右索引),如果无效,则返回nullptr。
根据前序遍历的首元素确定根节点,然后在中序遍历中找到根节点的位置,从而确定左右子树的范围。
计算左子树的大小,然后递归构造左子树和右子树。
最后,将构造好的左右子树分别连接到根节点的左右指针上,并返回根节点。

106. 从中序与后序遍历序列构造二叉树
给定两个整数数组
inorder和postorder,其中inorder是二叉树的中序遍历,postorder是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。示例 1:
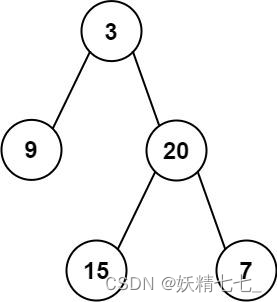
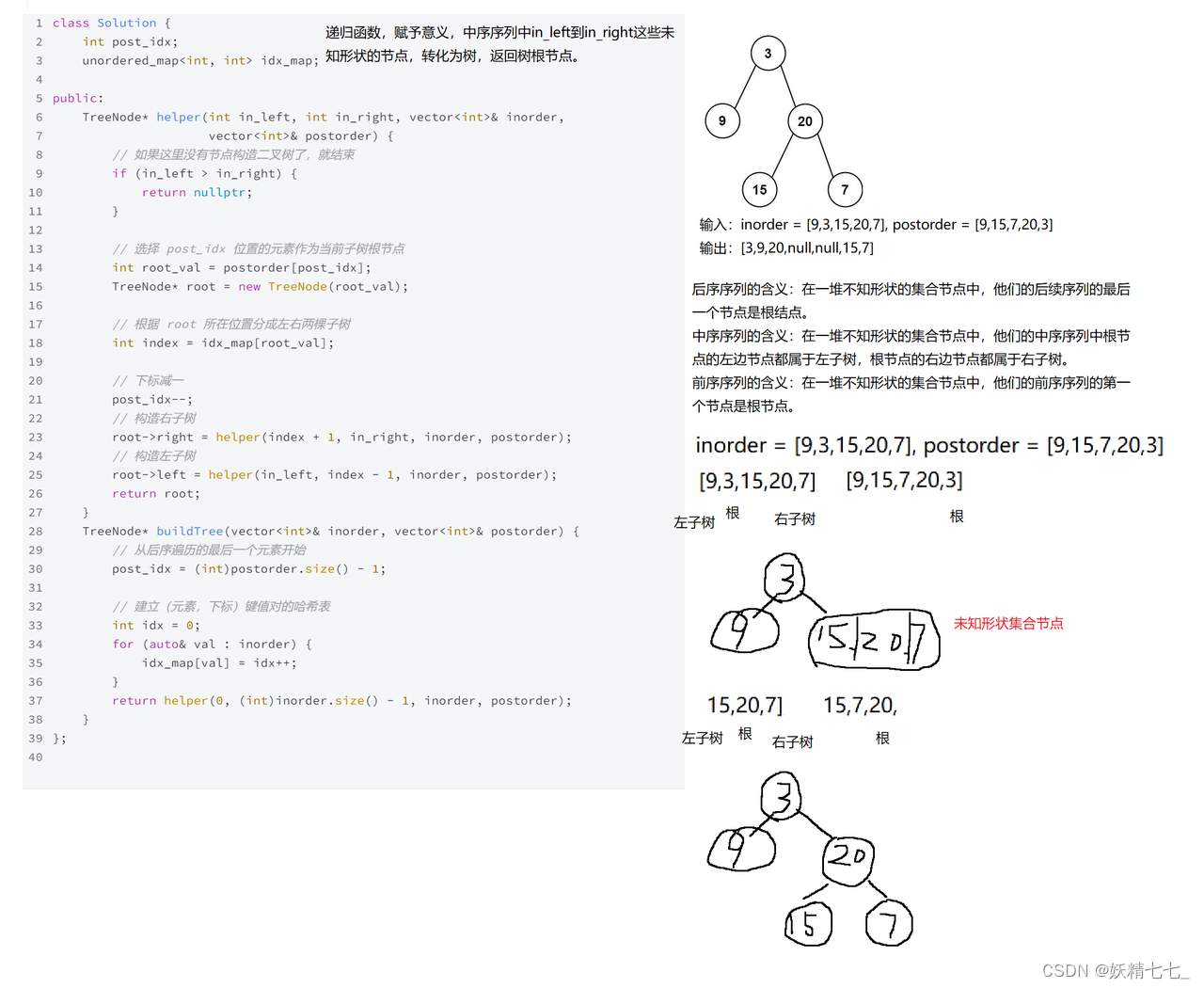
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] 输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1] 输出:[-1]
提示:
1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder和postorder都由 不同 的值组成
postorder中每一个值都在inorder中
inorder保证是树的中序遍历
postorder保证是树的后序遍历
class Solution {int post_idx;unordered_map<int, int> idx_map;public:TreeNode* helper(int in_left, int in_right, vector<int>& inorder,vector<int>& postorder) {// 如果这里没有节点构造二叉树了,就结束if (in_left > in_right) {return nullptr;}// 选择 post_idx 位置的元素作为当前子树根节点int root_val = postorder[post_idx];TreeNode* root = new TreeNode(root_val);// 根据 root 所在位置分成左右两棵子树int index = idx_map[root_val];// 下标减一post_idx--;// 构造右子树root->right = helper(index + 1, in_right, inorder, postorder);// 构造左子树root->left = helper(in_left, index - 1, inorder, postorder);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {// 从后序遍历的最后一个元素开始post_idx = (int)postorder.size() - 1;// 建立(元素,下标)键值对的哈希表int idx = 0;for (auto& val : inorder) {idx_map[val] = idx++;}return helper(0, (int)inorder.size() - 1, inorder, postorder);}
};
buildTree 函数:
作为类的公共接口,这个函数接收两个数组:一个是树的中序遍历结果inorder,另一个是后序遍历结果postorder。
初始化post_idx为后序遍历数组的最后一个元素的索引,这个元素是树的根节点。
使用inorder数组的元素建立一个哈希表idx_map,用于快速查找中序遍历中元素的索引。
调用helper函数来构建并返回树的根节点。
helper 函数:
递归函数,用于根据给定的中序遍历和后序遍历的某一部分来构造子树,并返回子树的根节点。
参数in_left和in_right定义了当前子树在中序遍历中的范围。
如果in_left大于in_right,说明没有节点可以用来构建子树,返回nullptr。
使用postorder[post_idx]确定当前子树的根节点,并据此在中序遍历中找到根节点的索引index。
递归构建右子树和左子树。注意,必须先构建右子树,因为在后序遍历中,根节点之前的元素是先遍历右子树再遍历左子树的。
144. 二叉树的前序遍历 - 力扣(LeetCode)
给你二叉树的根节点
root,返回它节点值的 前序 遍历。示例 1:
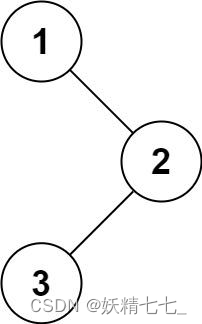
输入:root = [1,null,2,3] 输出:[1,2,3]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [1] 输出:[1]
示例 4:
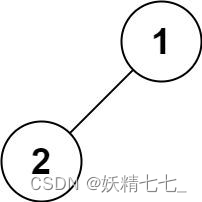
输入:root = [1,2] 输出:[1,2]
示例 5:
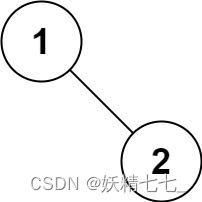
输入:root = [1,null,2] 输出:[1,2]
提示:
树中节点数目在范围
[0, 100]内
-100 <= Node.val <= 100进阶:递归算法很简单,你可以通过迭代算法完成吗?
class Solution {
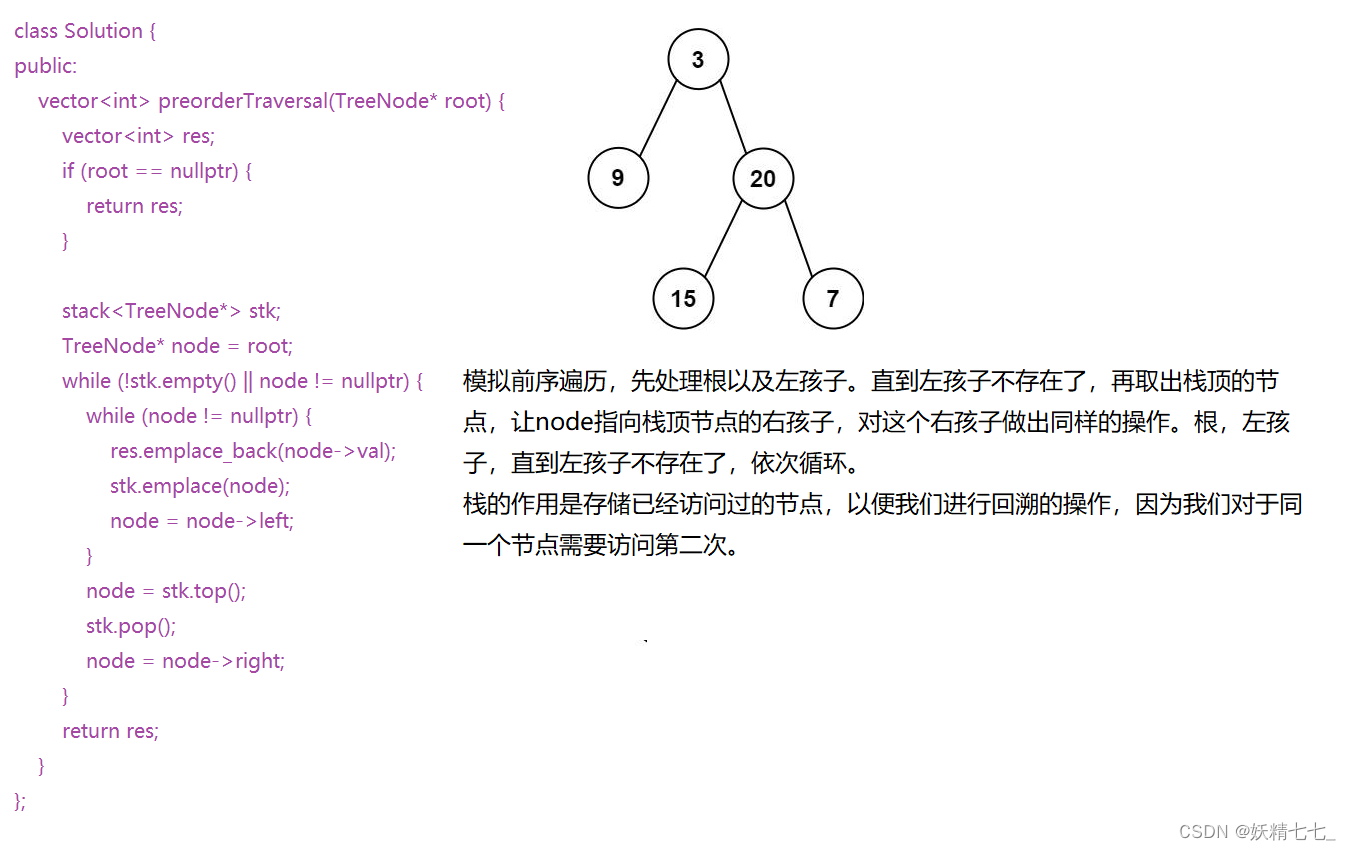
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> res;if (root == nullptr) {return res;}stack<TreeNode*> stk;TreeNode* node = root;while (!stk.empty() || node != nullptr) {while (node != nullptr) {res.emplace_back(node->val);stk.emplace(node);node = node->left;}node = stk.top();stk.pop();node = node->right;}return res;}
};
前序遍历的顺序是先访问根节点,然后遍历左子树,最后遍历右子树。这里使用了迭代的方法而不是递归,主要依靠栈(stack)来实现。
定义一个名为preorderTraversal的函数,它接受一个指向TreeNode类型的指针root作为参数,表示二叉树的根节点。函数返回一个整数向量(vector<int>),包含树的前序遍历结果。
定义一个名为res的整数向量,用来存储遍历过程中节点的值,也就是前序序列的输出结果。
检查根节点是否为nullptr,如果是,表示树为空,直接返回空的res向量。
定义一个栈stk,用来存储节点的指针。这个栈帮助我们在遍历过程中回溯到之前的节点。栈内存放的节点表示已经访问过一次的节点,也就是第二次待访问的节点。
定义一个指针node,初始化为根节点root。这个指针将用来遍历树。
外循环继续执行,直到栈为空且node指针为nullptr。这意味着树已经被完全遍历。
while (node != nullptr) {res.emplace_back(node->val);stk.emplace(node);node = node->left;}
这个内层循环遍历到当前子树的最左边的节点,沿途经过的每个节点都被处理并压入栈中。
将当前节点的值添加到res向量中。这符合前序遍历中“根节点-左子树-右子树”的顺序。第一次访问节点是访问该节点的根。存放到res向量中。
将当前节点压入栈中,以便后续能够回溯到其父节点。栈内的节点表示已经访问过一次的节点,也就是第二次访问待访问的节点。
将node指针移动到当前节点的左子节点,继续前序遍历过程。
node = stk.top();stk.pop();node = node->right;
当到达最左边的节点(node为nullptr)时,从栈中取出最近一个还未处理其右子树的节点。
将node指针移动到刚刚从栈中取出的节点的右子节点,然后继续循环,进行右子树的遍历。
在树被完全遍历后,返回包含前序遍历结果的res向量。
94. 二叉树的中序遍历 - 力扣(LeetCode)
给定一个二叉树的根节点
root,返回 它的 中序 遍历 。示例 1:
输入:root = [1,null,2,3] 输出:[1,3,2]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [1] 输出:[1]
提示:
树中节点数目在范围
[0, 100]内
-100 <= Node.val <= 100进阶: 递归算法很简单,你可以通过迭代算法完成吗?
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> res;stack<TreeNode*> stk;while (root != nullptr || !stk.empty()) {while (root != nullptr) {stk.push(root);root = root->left;}root = stk.top();stk.pop();res.push_back(root->val);root = root->right;}return res;}
};
定义了一个名为inorderTraversal的函数,它接收一个指向TreeNode类型的指针root作为参数,表示二叉树的根节点。函数返回一个整数向量(vector<int>),包含树的中序遍历结果。
定义一个名为res的整数向量,用来存储遍历过程中节点的值。
定义一个栈stk,用于存储节点指针。这个栈帮助我们在遍历过程中回溯到之前的节点。
这个循环继续执行,直到root指针为空且栈为空。这意味着树已经被完全遍历。
这个内层循环遍历到当前子树的最左边的节点,并将沿途经过的每个节点压入栈中。
while (root != nullptr) {stk.push(root);root = root->left;}
将当前节点压入栈中。这一步确保了我们可以在完成左子树的遍历后,回到当前节点。
将root指针移动到当前节点的左子节点,继续中序遍历的过程。
root = stk.top();stk.pop();res.push_back(root->val);root = root->right;
当到达最左边的节点时(即root为nullptr),从栈中取出最近一个还未访问其值的节点。
将从栈中取出的节点的值添加到res向量中。这一步是在访问节点的值,符合中序遍历的顺序。
将root指针移动到刚刚访问过的节点的右子节点,然后继续循环,以遍历右子树。
在树被完全遍历后,返回包含中序遍历结果的res向量。
145. 二叉树的后序遍历 - 力扣(LeetCode)
给你一棵二叉树的根节点
root,返回其节点值的 后序遍历 。示例 1:
输入:root = [1,null,2,3] 输出:[3,2,1]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [1] 输出:[1]
提示:
树中节点的数目在范围
[0, 100]内
-100 <= Node.val <= 100进阶:递归算法很简单,你可以通过迭代算法完成吗?
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> res;if (root == nullptr) {return res;}stack<TreeNode*> stk;TreeNode* prev = nullptr;while (root != nullptr || !stk.empty()) {while (root != nullptr) {stk.emplace(root);root = root->left;}root = stk.top();stk.pop();if (root->right == nullptr || root->right == prev) {res.emplace_back(root->val);prev = root;root = nullptr;} else {stk.emplace(root);root = root->right;}}return res;}
};
这行代码定义了一个名为postorderTraversal的函数,它接收一个指向TreeNode类型的指针root作为参数,表示二叉树的根节点。函数返回一个整数向量(vector<int>),包含树的后序遍历结果。
定义一个名为res的整数向量,用来存储遍历过程中节点的值
这段代码检查根节点是否为nullptr,如果是,表示树为空,直接返回空的res向量。
定义一个栈stk,用来存储节点的指针。这个栈帮助我们在遍历过程中回溯到之前的节点。
定义一个指针prev,初始化为nullptr。这个指针用来记录最近访问过的节点,以便判断是否可以访问当前节点的右子节点或是应该访问当前节点(在后序遍历中,一个节点在其右子节点被访问后才被访问)。
这个循环继续执行,直到root指针为nullptr且栈为空。这意味着树已经被完全遍历。
while (root != nullptr) {stk.emplace(root);root = root->left;}
这个内层循环遍历到当前子树的最左边的节点,沿途经过的每个节点都被压入栈中。
将当前节点压入栈中,以便后续能够回溯到其父节点。
将root指针移动到当前节点的左子节点,继续遍历过程。
root = stk.top();stk.pop();
当到达最左边的节点(root为nullptr时),从栈中取出最近一个还未处理其右子树或自身的节点。
if (root->right == nullptr || root->right == prev) {res.emplace_back(root->val);prev = root;root = nullptr;} else {stk.emplace(root);root = root->right;}
对于栈内的每一个节点,先访问左子树,第一次入栈表示的是已经访问过一次的节点,第二次访问就是出栈,判断是否可以直接输出,如果不能直接输出又将该节点入栈,但是我们入的是同一个栈,如何表示是该节点是第三次访问还是第二次访问,就看prev上一个输出的节点是什么,如果上一个输出的节点是右孩子,说明这个节点是第三次访问。此时直接输出即可。
这个条件判断当前节点的右子节点是否不存在或已经被访问。如果是,那么可以访问当前节点。
将当前节点的值添加到res向量中。这符合后序遍历中“左子树-右子树-根节点”的顺序。
更新prev指针为刚刚访问过的节点。
将root指针设置为nullptr,这表示当前节点已处理完毕,下一次循环将从栈顶节点继续执行。
如果当前节点的右子节点存在且未被访问,则将当前节点再次压入栈中,并将root指针移动到右子节点,继续遍历过程。
在树被完全遍历后,返回包含后序遍历结果的res向量。
结尾
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!



)











)


)
