目录
1. 翻译环境和运行环境
2. 翻译环境
2.1 预处理
2.2 编译
2.3 汇编
2.4 链接
3. 运行环境
4.完结散花
悟已往之不谏,知来者犹可追
创作不易,宝子们!如果这篇文章对你们有帮助的话,别忘了给个免费的赞哟~
1. 翻译环境和运行环境
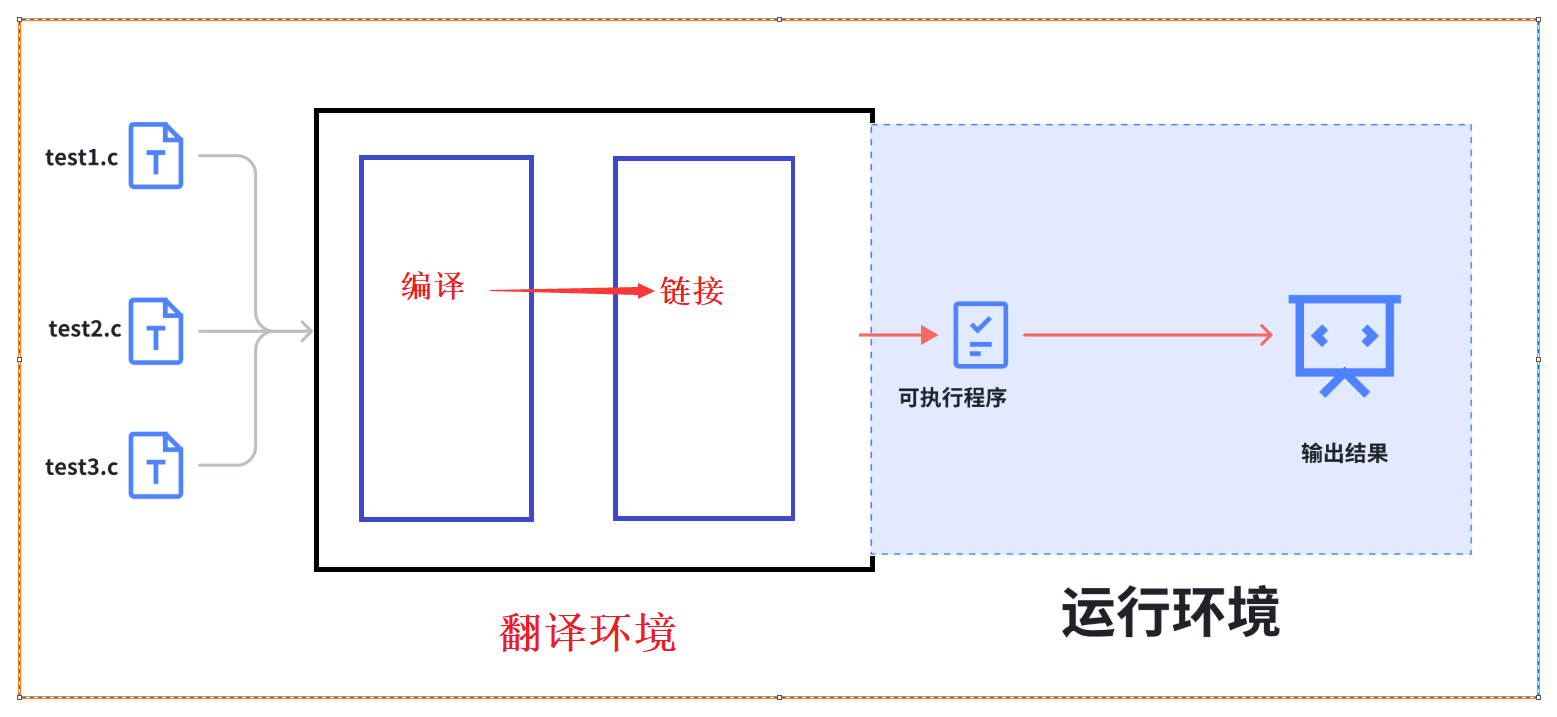
在ANSI C的任何一种实现中,存在两个不同的环境~
其一:翻译环境
在这个环境中源代码被翻译(转化)成可执行的机器指令(即二进制指令)
其二:执行环境
用于实际执行代码
2. 翻译环境
那么翻译环境是怎么将源代码转化成可执行的机器指令呢~
其实翻译环境是由编译和链接两个大的过程组成的,而编译过程又可以分为由三个过程:预处理(有些书也叫预编译)、编译和汇编。
一个C语言项目可能有多个.c文件一起构成,那多个.c文件是如何生成可执行程序的呢?
1.多个.c文件单独经过编译器,编译处理生成对应的目标文件
2.注:在Windows环境下目标文件的后缀是.obj,而在Linux环境下目标文件的后缀是.o
3.多个目标文件和链接库一起经过链接器处理最终生成可执行的程序~
4.链接库是指运行时库(它是支持程序运行的基本函数集合)或者第三方库~
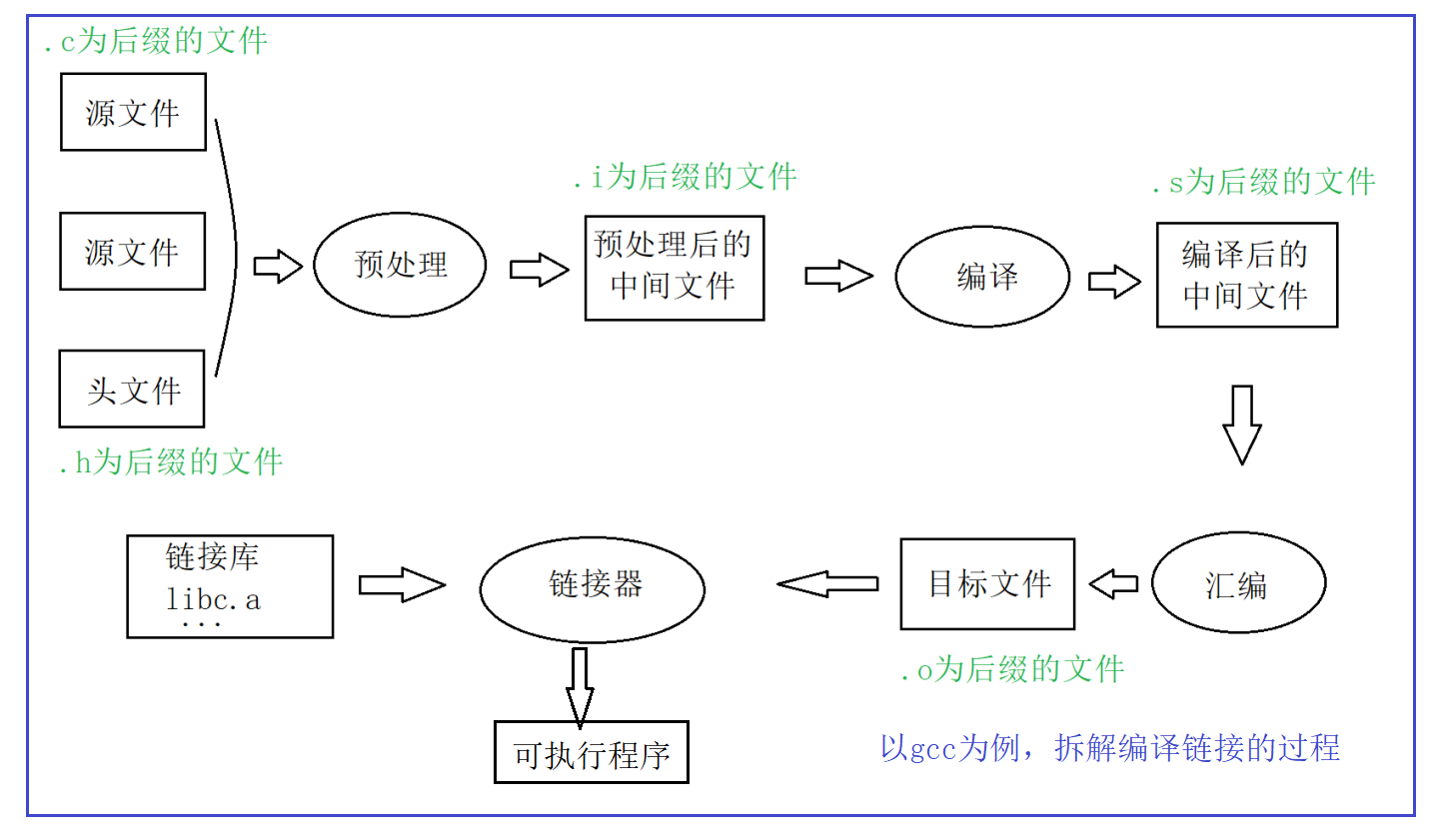
如果再把编译器分成三个过程,那就变成了下面的过程~
2.1 预处理
在预处理阶段,源文件和头文件会被处理为.i为后缀的文件
在gcc环境下想观察一下,对test.c预处理后的.i文件,命令如下~
gcc -E test.c -o test.i预处理阶段主要处理那些源文件中#开始的预编译指令,比如:#include,#define,处理的规则如下:
•将所有的#define删除,并展开所有的宏定义。
•处理所有的条件编译指令,如:#if、#ifdef、#elif、#else、#endif
• 处理#include预编译指令,将包含的头文件的内容插入到该预编译指令的位置。这个过程是递归进行的,也就是说被包含的头文件也可能包含其他文件。
• 删除所有的注释
• 添加行号和文件名标识,方便后续编译器生成调试信息等。
• 或保留所有的#pragma的编译器指令,编译器后续会使用。
经过预处理后的.i文件中不再包含宏定义,因为宏已经被展开。并且包含的头文件都被插如到.i文件
中。所以当我们无法知道宏定义或者头文件是否包含正确的时候,可以查看预处理后的.i文件来确认。
2.2 编译
编译过程就是将预处理后的.i文件进行一系列的:词法分析、语法分析、语义分析及优化,生成相应的汇编代码文件。
编译过程的命令如下:
gcc -S test.i -o test.s词法分析:
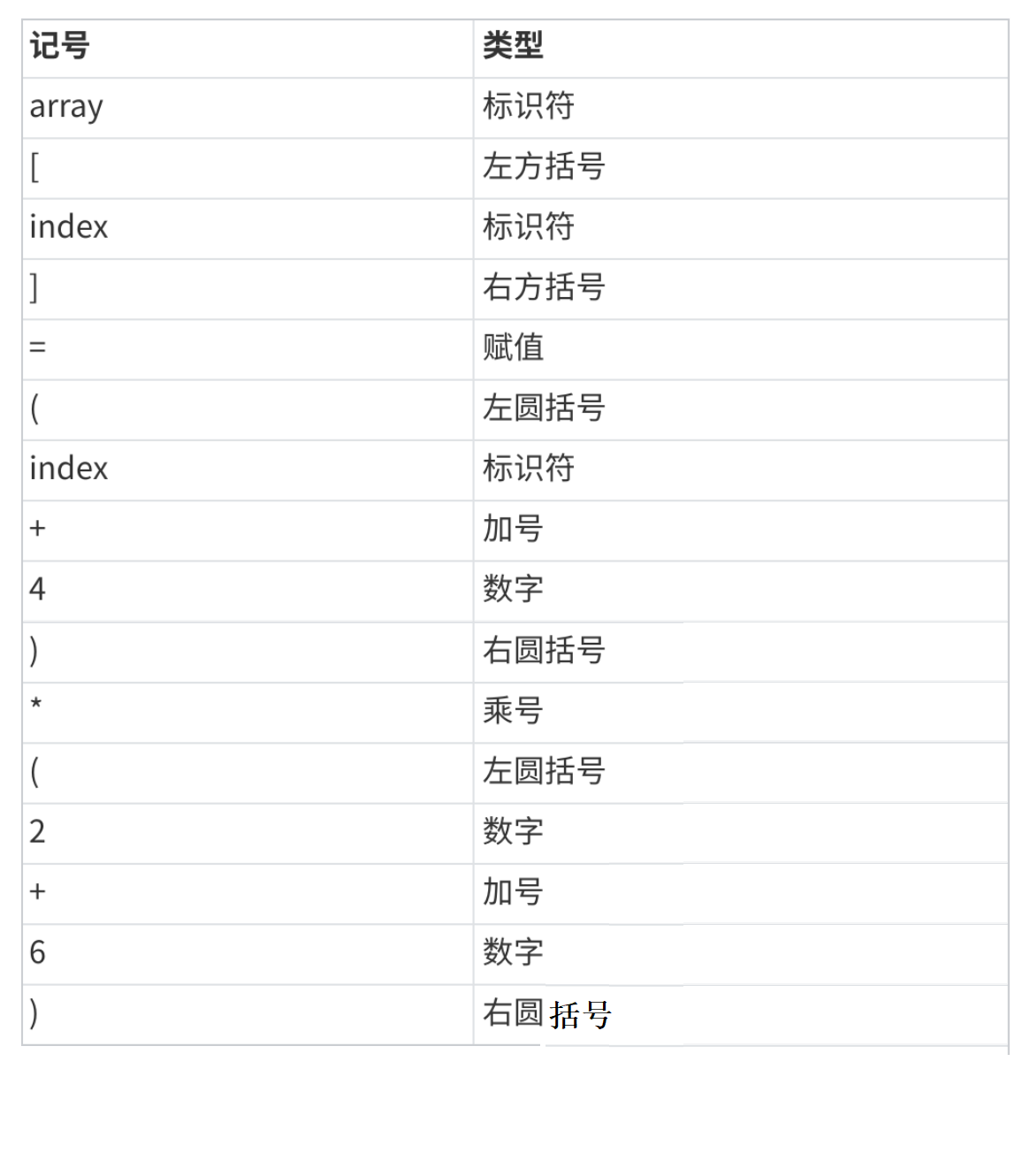
将源代码程序被输⼊扫描器,扫描器的任务就是简单的进行词法分析,把代码中的字符分割成⼀系列的记号(关键字、标识符、字⾯量、特殊字符等)。
上面程序进行词法分析后得到了16个记号:
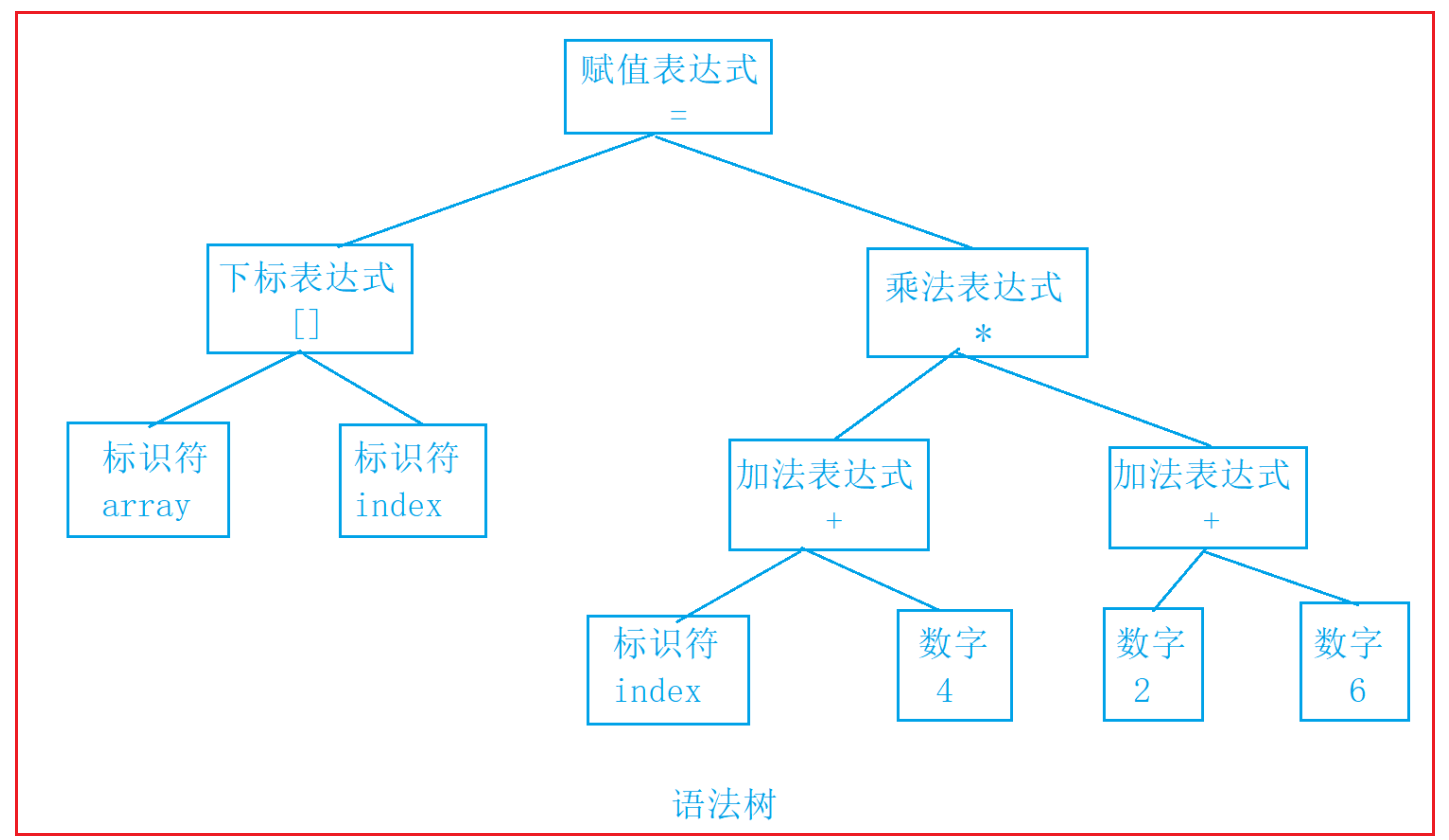
语法分析 :
接下来语法分析器,将对扫描产生的记号进行语法分析,从而产生语法树。这些语法树是以表达式为节点的树
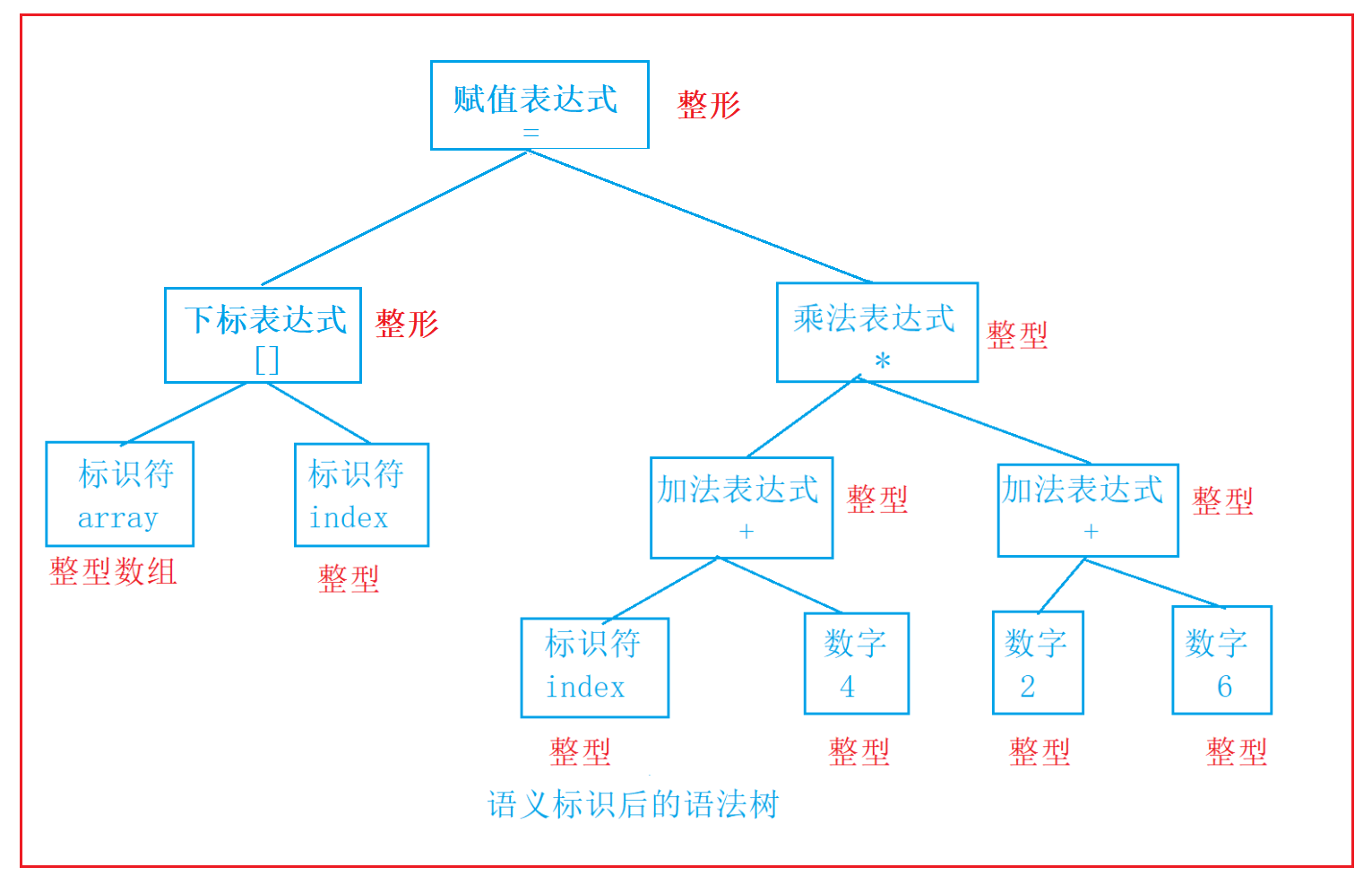
语义分析:
由语义分析器来完成语义分析,即对表达式的语法层面分析。编译器所能做的分析是语义的静态分
析。静态语义分析通常包括声明和类型的匹配,类型的转换等。这个阶段会报告错误的语法信息
2.3 汇编
汇编器是将汇编代码转转变成机器可执行的指令,每⼀个汇编语句几乎都对应⼀条机器指令。就是根据汇编指令和机器指令的对照表⼀⼀的进行翻译,也不做指令优化。
汇编的命令如下:
gcc -c test.s -o test.o2.4 链接
链接是⼀个复杂的过程,链接的时候需要把⼀堆文件链接在⼀起才生成可执行程序。
链接过程主要包括:地址和空间分配,符号决议和重定位等这些步骤。
链接解决的是⼀个项目中多文件、多模块之间互相调用的问题
比如:
在⼀个C的项目中有2个.c文件( test.c 和 add.c ),代码如下:
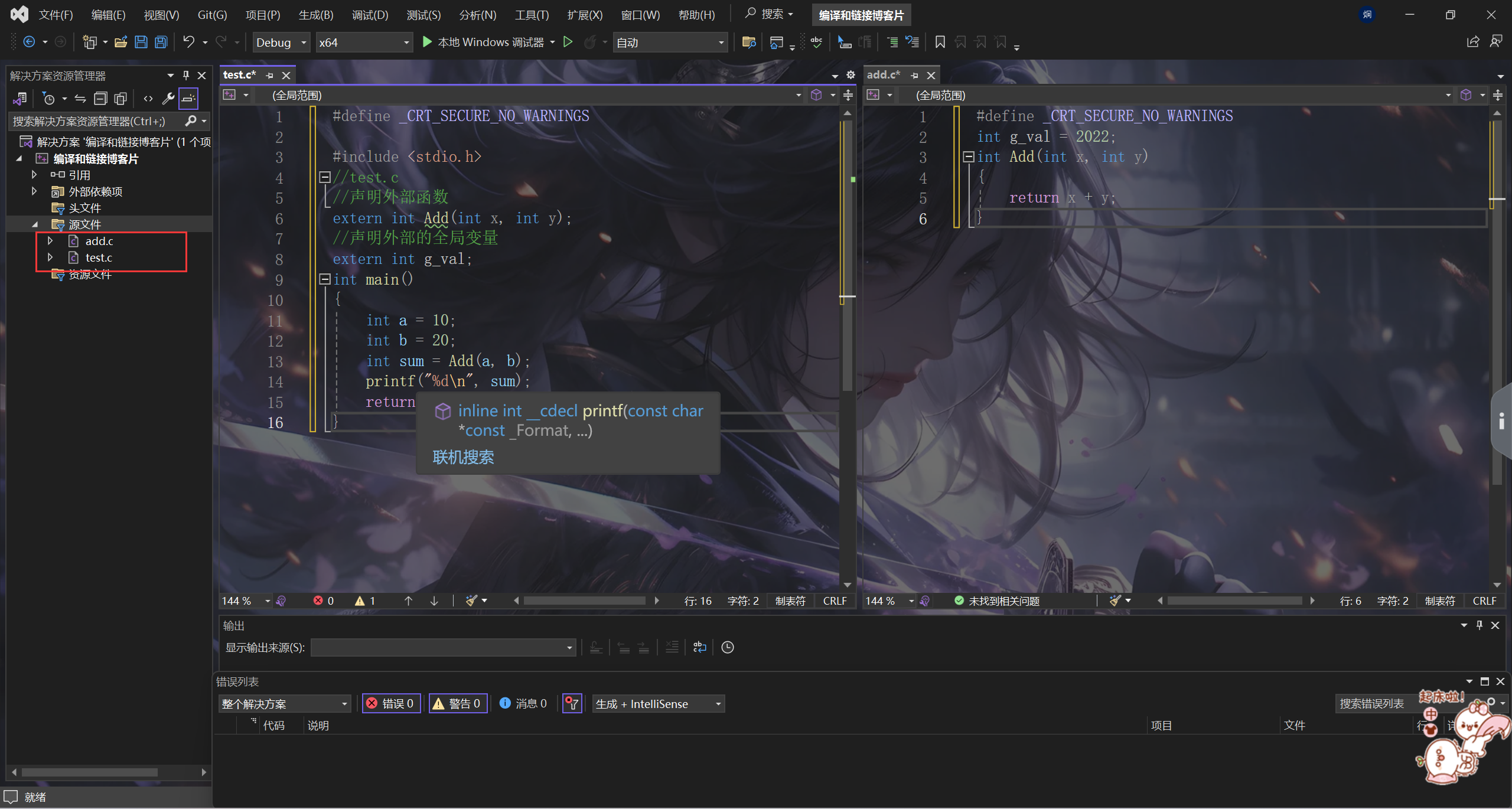
test.c
#include <stdio.h> //test.c //声明外部函数 extern int Add(int x, int y); //声明外部的全局变量 extern int g_val; int main() { int a = 10; int b = 20; int sum = Add(a, b); printf("%d\n", sum); return 0; }
add.c
int g_val = 2022; int Add(int x, int y) { return x+y; }
我们已经知道,每个源文件都是单独经过编译器处理生成对应的目标文件。
test.c 经过编译器处理生成 test.o
add.c 经过编译器处理生成 add.o
我们在 test.c 的文件中使用了 add.c ⽂件中的 Add 函数和 g_val 变量。
我们在 test.c 文件中每⼀次使用Add 函数和 g_val 的时候必须确切的知道 Add 和 g_val 的地
址,但是由于每个⽂件是单独编译的,在编译器编译 test.c 的时候并不知道 Add 函数和 g_val
变量的地址,所以暂时把调用 Add 的指令的目标地址和 g_val 的地址搁置。等待最后链接的时候由链接器根据引用的符号 Add 在其他模块中查找 Add 函数的地址,然后将 test.c 中所有引用到
Add 的指令重新修正,让他们的目标地址为真正的 Add 函数的地址,对于全局变量 g_val 也是类
似的方法来修正地址。这个地址修正的过程也被叫做:重定位。
3. 运行环境
1. 程序必须载⼊内存中。在有操作系统的环境中:⼀般这个由操作系统完成。在独⽴的环境中,程序的载⼊必须由⼿⼯安排,也可能是通过可执⾏代码置⼊只读内存来完成。
2. 程序的执⾏便开始。接着便调⽤main函数。
3. 开始执⾏程序代码。这个时候程序将使⽤⼀个运⾏时堆栈(stack),存储函数的局部变量和返回地址。程序同时也可以使⽤静态(static)内存,存储于静态内存中的变量在程序的整个执⾏过程⼀直保留他们的值。
4. 终⽌程序。正常终⽌main函数;也有可能是意外终⽌。
4.完结散花
好了,这期的分享到这里就结束了~
如果这篇博客对你有帮助的话,可以用你们的小手指点一个免费的赞并收藏起来哟~
如果期待博主下期内容的话,可以点点关注,避免找不到我了呢~
我们下期不见不散~~





)
(附MATLAB代码实现))








devops持续集成开发——使用docker安装部署jenkins流水线服务)


>)




