登录—专业IT笔试面试备考平台_牛客网

using i64 = long long;
using ll = long long;
constexpr ll M = 1e9 + 7;
template<class Info>
struct SegmentTree {int n;std::vector<Info> info;SegmentTree() : n(0) {}SegmentTree(int n_, Info v_ = Info()) {init(n_, v_);}template<class T>SegmentTree(std::vector<T> init_) {init(init_);}void init(int n_, Info v_ = Info()) {init(std::vector<Info>(n_, v_));}template<class T>void init(std::vector<T> init_) {n = init_.size();info.assign(4 << (int)std::log2(n), Info());std::function<void(int, int, int)> build = [&](int p, int l, int r) {if (r - l == 1) {info[p] = init_[l];return;}int m = (l + r) / 2;build(2 * p, l, m);build(2 * p + 1, m, r);pull(p);};build(1, 0, n);}void pull(int p) {info[p] = info[2 * p] + info[2 * p + 1];}void modify(int p, int l, int r, int x, const Info& v) {if (r - l == 1) {info[p] = v;return;}int m = (l + r) / 2;if (x < m) {modify(2 * p, l, m, x, v);}else {modify(2 * p + 1, m, r, x, v);}pull(p);}void modify(int p, const Info& v) {modify(1, 0, n, p, v);}Info rangeQuery(int p, int l, int r, int x, int y) {if (l >= y || r <= x) {return Info();}if (l >= x && r <= y) {return info[p];}int m = (l + r) / 2;return rangeQuery(2 * p, l, m, x, y) + rangeQuery(2 * p + 1, m, r, x, y);}Info rangeQuery(int l, int r) {return rangeQuery(1, 0, n, l, r);}template<class F>int findFirst(int p, int l, int r, int x, int y, F pred) {if (l >= y || r <= x || !pred(info[p])) {return -1;}if (r - l == 1) {return l;}int m = (l + r) / 2;int res = findFirst(2 * p, l, m, x, y, pred);if (res == -1) {res = findFirst(2 * p + 1, m, r, x, y, pred);}return res;}template<class F>int findFirst(int l, int r, F pred) {return findFirst(1, 0, n, l, r, pred);}template<class F>int findLast(int p, int l, int r, int x, int y, F pred) {if (l >= y || r <= x || !pred(info[p])) {return -1;}if (r - l == 1) {return l;}int m = (l + r) / 2;int res = findLast(2 * p + 1, m, r, x, y, pred);if (res == -1) {res = findLast(2 * p, l, m, x, y, pred);}return res;}template<class F>int findLast(int l, int r, F pred) {return findLast(1, 0, n, l, r, pred);}
};struct Info {ll a;//表示黄色砖块,当前ll b;ll c = 1;ll d;
};Info operator+(const Info& b, const Info& a) {//b.a + a.a * b.c//b.b + a.a * b.d + a.b //a.c * b.c//a.c * b.d + a.d return { (b.a + ((a.a%M) * (b.c%M))%M)%M, (b.b + ((a.a%M) * (b.d%M)) + a.b)%M, ((a.c%M) * (b.c%M))%M, (((a.c%M) * (b.d%M)%M) + a.d)%M };
}Info Y{ 0, 0, 1, 1 };
Info B{ 1, 0, 0, 1 };//箭头指向下一个位置
Info R{ 0, 0, 2, 1 };//总数量乘以2在加上一个红色砖块int main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);int n, q;std::cin >> n >> q;std::string s;std::cin >> s;//最底层的n个区间,比如[0,1)表示第一个区间,代表第一块砖SegmentTree<Info> seg(n);for (int i = 0; i < n; i++) {seg.modify(i, (s[i] == 'Y') ? Y : ((s[i] == 'B') ? B : R));/*for (int j = 0; j < n; j++) {Info t = seg.rangeQuery(j, j + 1);std::cout <<j<<":"<< t.a << ' ' << t.b << ' ' << t.c << ' ' << t.d << '\n';}*/}while (q--) {int o;std::cin >> o;if (o == 1) {int p;char c;std::cin >> p >> c;p--;seg.modify(p, (c == 'Y') ? Y : ((c == 'B') ? B : R));}else {int l, r;std::cin >> l >> r;l--;Info res = seg.rangeQuery(l, r);//b和d的和为总数ll ans = (res.b + res.d) % M;std::cout << ans << "\n";}}return 0;
}

第一点:std::vector<Info> info;存的是按区间字符操作后的效果,有点难理解,举个例子,如果你查询[0,1)这个区间相当于查询按第一个字符进行游戏后的效果,如果第一个字符是Y,那么查询的结果就是Info Y{ 0, 0, 1, 1 };至于Info为什么要这么定义我们来看看下面的内容.

其中最难理解的就是下面这一部分

struct Info {ll a;//最左边的柱子的倍数ll b;//所有累计的方块ll c = 1;//现有倍数ll d;//现有这一列的方块
};Info operator+(const Info& b, const Info& a) {//b.a + a.a * b.c//b.b + a.a * b.d + a.b//a.c * b.c//a.c * b.d + a.d return { (b.a + ((a.a%M) * (b.c%M))%M)%M, (b.b + ((a.a%M) * (b.d%M)) + a.b)%M, ((a.c%M) * (b.c%M))%M, (((a.c%M) * (b.d%M)%M) + a.d)%M };
}Info Y{ 0, 0, 1, 1 };
Info B{ 1, 0, 0, 1 };//箭头指向下一个位置
Info R{ 0, 0, 2, 1 };//总数量乘以2在加上一个红色砖块

首先a,b,c,d的意思我都标出来了,为什么要这么定义呢,我们这样想,当中间有很多个操作B出现的时候,那么这个区间是不是有很多个柱子,这样不清楚,让我来画个图

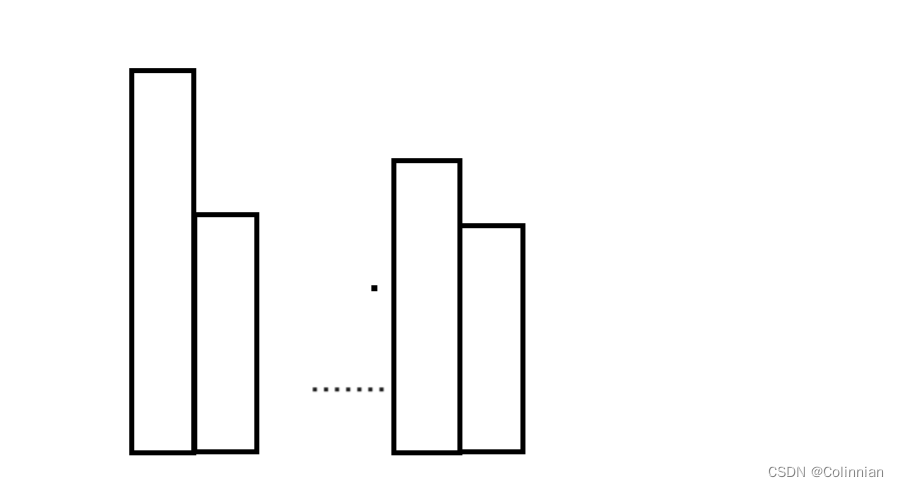
如果产生了多个柱子是不是说明有操作B,第一个柱子不管是YRRY或是什么其它的操作它都不可能产生第二个柱子.假如我们要合并两个区间,

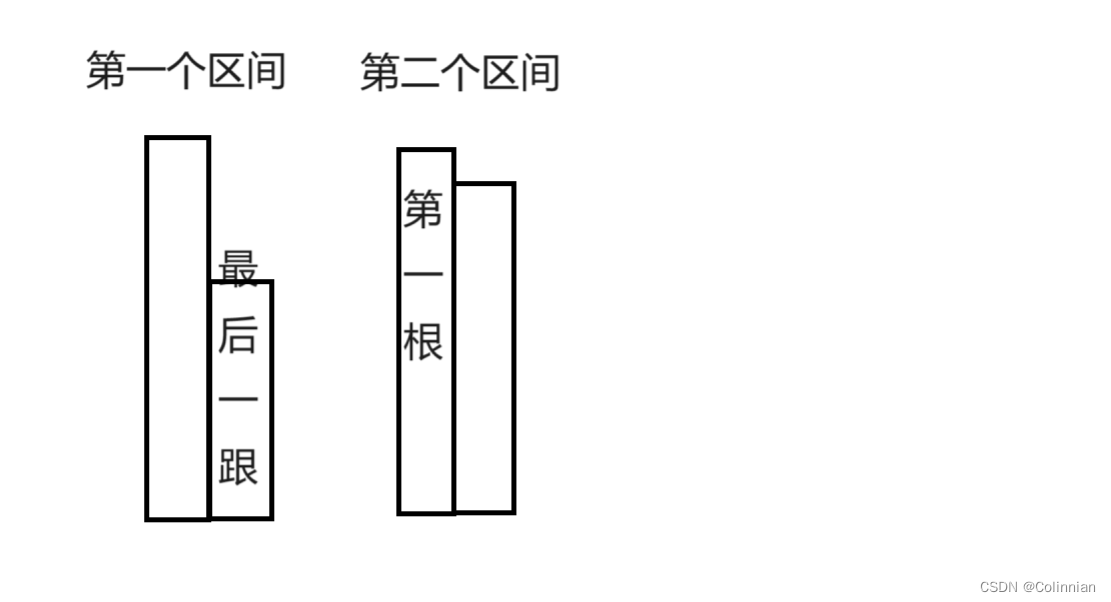
每根柱子表示的无非就是YR的组合,可能是YYYY,RRRR又或者是YRRY等等,不存在B所以最后一根和第一根合并的序列一定是一根,那么效果是怎样的呢, 显然最后一根总方块数我们可以设为k,那么合并后可以表示为((k+a1)*2+a2)*2+a3,原先第一根的方块数为(a1*2+a2)*2+a3,两者的差值不就是把k提到外面来吗及(a1*2+a2)*2+a3+4*k(注意,我只是举了一个只有两个R情况下的例子,*2的数量要根据R的数量来定),那么+重载为什么这样运算也很明显了.

对于第一个算式b.a + a.a * b.c,再使用B之前,第一根的方块数量和R的数量是不确定的,如果第一个区间有B,那么第一个区间的c变量是0,也就是说两个区间合并后的第一根倍数就是b.a,如果第一个区间没有B,说明第二个区间的第一根和第一个区间合并后会变成一根,即b.c不为0而b.a为0,合并后的第一根是a.a乘以b.c.

感觉解释的不是很清楚(*/ω＼*),换个解释方法,Info Y{ 0, 0, 1, 1 };第一个1表示当前倍数为自己身的一倍,也就是不翻倍,第二个1表示添加到目前这根柱子里添加一个方块,Info R{ 0, 0, 2, 1 };翻倍后添加,Info B{ 1, 0, 0, 1 };这涉及到好几个运算,首先看最简单的a.c*b.c表示第一根柱子已经固定了,根据之前讲的最后一根和第一根合并的运算,我们要把当前倍数转移到a变量里,及a.a * b.c,因为b是左边的区间,所以按照这个运算,如果它在之前有过B字符,那么它也不为0,所以要加上b.a.

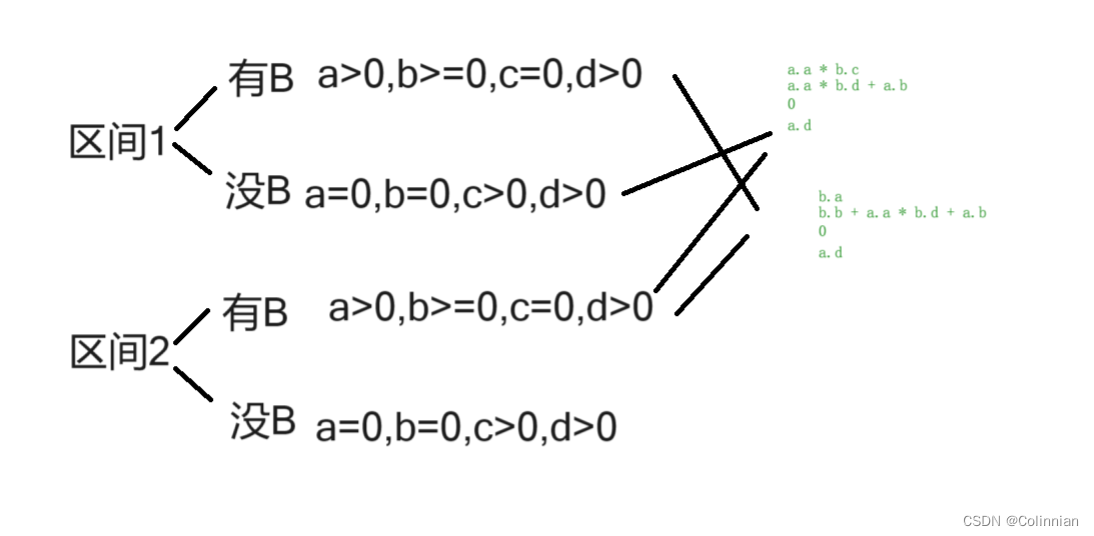
列举了两个,其它的是一样的,就像是自动机一样,涉及到有B和没B的情况,比较难解释,当涉及B的时候某些变量会自动变为0从而做出变换.

b.a(有B/没B) + a.a(有B/没B) * b.c(没B/有B)
b.b(有B/没B) + a.a(有B/没B) * b.d + a.b(有B/没B)         有Ba.a会把b.d添加到非当前柱子
a.c * b.c(没B/有B)
a.c(没B/有B) * b.d + a.d        没有B的时候a.c会把b.d添加到当前柱子 

大概就是这样,尽力了,很难解释.