LeetCode 热题 100 | 二叉树（下）

1 114. 二叉树展开为链表

2 105. 从前序与中序遍历序列构造二叉树

3 437. 路径总和 III

菜鸟做题（即将返校版），语言是 C++

1 114. 二叉树展开为链表

题眼：展开后的单链表应该与二叉树 先序遍历 顺序相同。

而先序遍历就是指，先遍历左子树，再遍历右子树。题意所说的展开，无非就是让左子树插队到右子树的前面去。

解题思路：采用递归，对于每个节点，先将它的左子树链到右侧去，再让右子树链到左子树的后面。

思路说明图：

对于节点 “1”，绿色部分为其左子树，黄色部分为其右子树。我们需要做的就是：先将左子树链到 “1” 的右侧去，再让右子树链到左子树的后面。对于节点 “2”，同理。

class Solution {
public:void flatten(TreeNode* root) {if (!root) return;TreeNode * p = root->left;if (p) {while (p->right) {p = p->right;}TreeNode * q = root->right;root->right = root->left;root->left = nullptr; // heap-use-after-free on address 0x503000000138p->right = q;}flatten(root->right);}
};

说明：为了能使右子树链到左子树的屁股后面，我们需要找到左子树的屁股，代码如下。

while (p->right) {p = p->right;
}

坑点：题目中说 “左子指针始终为 null”，即移走左子树后，要把左子指针置为空指针，代码如下。

root->left = nullptr; // heap-use-after-free on address 0x503000000138

否则会出现注释中的报错。

2 105. 从前序与中序遍历序列构造二叉树

遍历特点：

前序：根节点 << 左子树 << 右子树
中序：左子树 << 根节点 << 右子树

因此，preorder 和 inorder 数组中的元素也呈现出上述排列规律。

思路说明图：

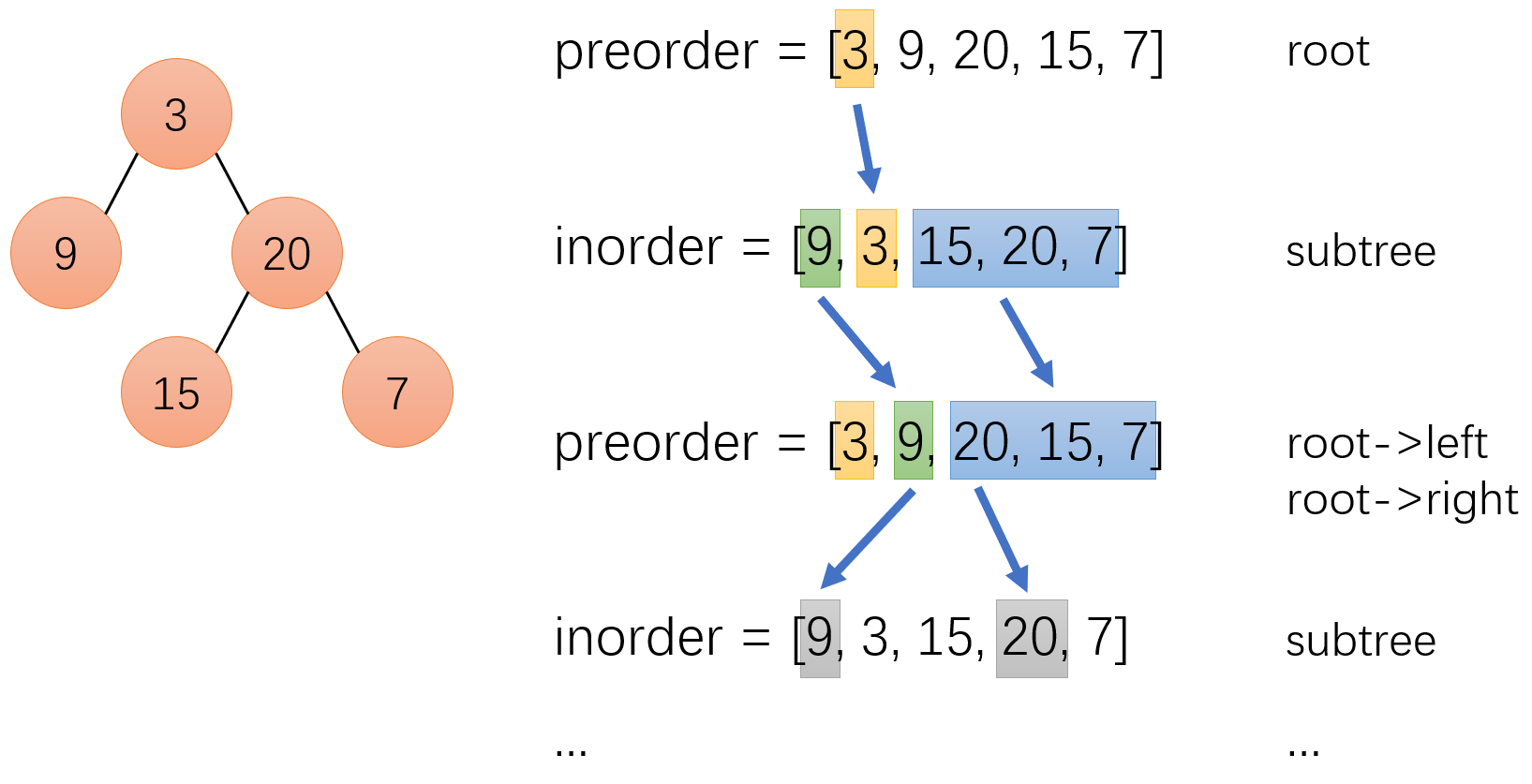
对于 preorder 数组，根据遍历特点，显然最左侧的 “3” 是根节点（root）。但是，我们无法根据 preorder 数组得知 “3” 的左子树和右子树分别是哪两坨。这时，inorder 数组就派上用场了。我们在 inorder 数组中定位 “3”，根据遍历特点，“3” 的左侧部分就是左子树（“9”），右侧部分就是右子树（“20” “15” “7”）。

现在，我们知道 “3” 的左子树和右子树分别是什么了，以及它们各自的长度。由此，我们可以在 preorder 数组中得到 “3” 的左子树和右子树所处的区间，即上图中的绿色部分和蓝色部分。又根据遍历特点，我们知道绿色部分的最左侧是左子树的根节点（root->left），蓝色部分的最左侧是右子树的根节点（root->right）。

以此类推，构造整个二叉树。

综上，preorder 数组的作用是定位各个根节点，inorder 数组的作用是定位左子树和右子树。

参数说明：

pre_left、pre_right：当前子树在 preorder 数组所处的区间
in_left、in_right：当前子树在 inorder 数组所处的区间
sub_ltree：左子树长度，帮助定位左子树区间

class Solution {
public:vector<int> preorder, inorder;unordered_map<int, int> hash;TreeNode * helper(int pre_left, int pre_right, int in_left, int in_right) {if (pre_left > pre_right) return nullptr;int pre_root = pre_left;int in_root = hash[preorder[pre_root]];int sub_ltree = in_root - in_left;TreeNode * node = new TreeNode(preorder[pre_root]);node->left = helper(pre_left + 1, pre_left + sub_ltree,in_left, in_root - 1);node->right = helper(pre_left + sub_ltree + 1, pre_right,in_root + 1, in_right);return node;}TreeNode* buildTree(vector<int>& arr1, vector<int>& arr2) {int n = arr1.size();preorder = arr1;inorder = arr2;for (int i = 0; i < n; ++i) {hash[inorder[i]] = i;}return helper(0, n - 1, 0, n - 1);}
};

3 437. 路径总和 III

关键字：深度搜索（先序遍历）+ 前缀和

我百度了一下，说它俩是一个意思。我觉得采用先序遍历是因为，它每次都是沿着一条直线去遍历的，而不是像中序遍历那样跳着遍历的。因此，先序遍历更符合题意。

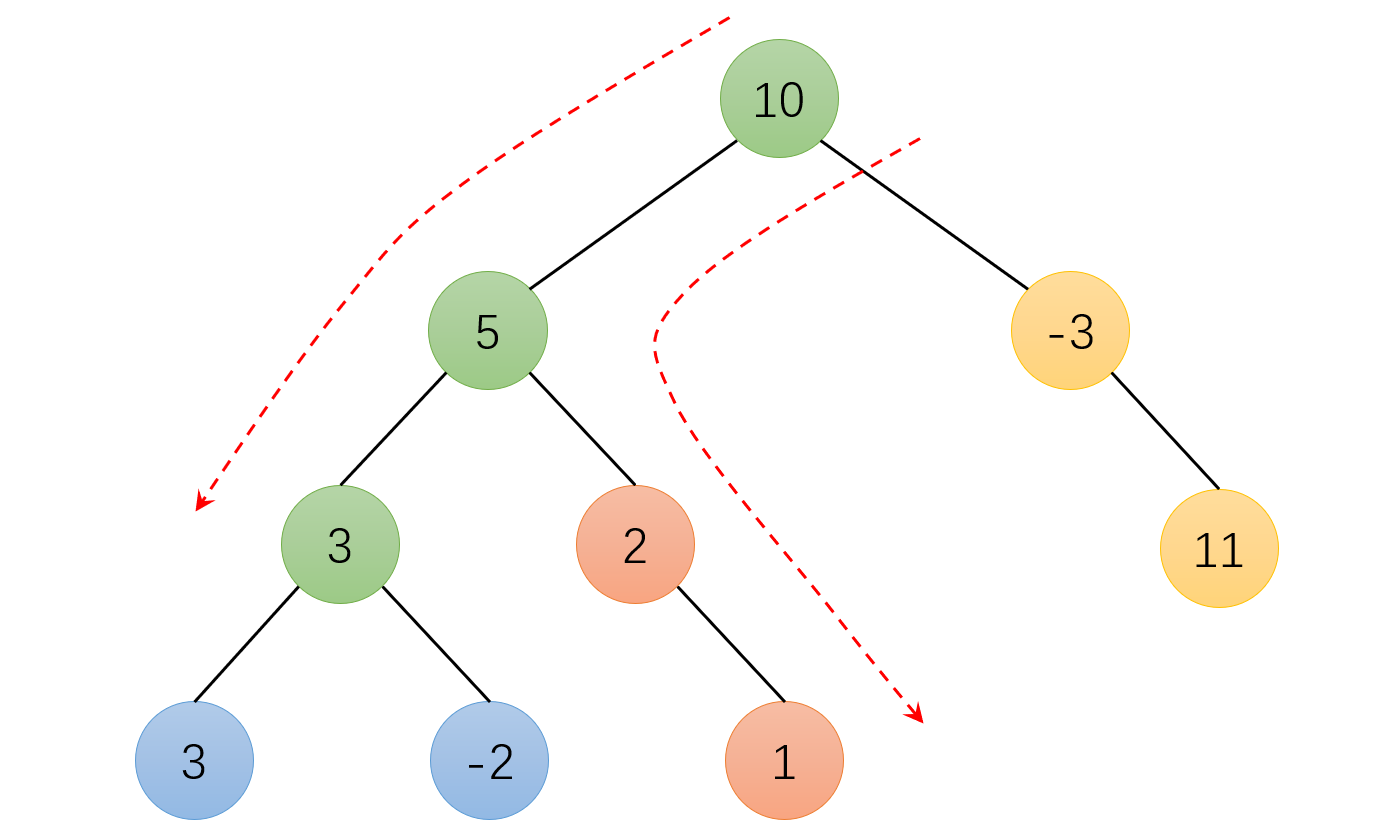
思路说明图：路径 “5, 3” 的和可以看作是路径 “10, 5, 3” 的和减去路径 “10” 的和，也就是可以转换为字符串那一节的前缀和问题。

这里说的前缀是指以根节点为开始的路径，而前缀和就是各个前缀的路径和。

具体解法：

① 定义变量

hash 用于存放各个前缀的路径和
total 用于记录当前加总出的路径和
count 用于记录符合条件的路径和的个数

② 查询符合条件的路径和

if (hash.count(total - targetSum)) {count = hash[total - targetSum];
}

就是在 hash 表中寻找，是否有前缀的路径和与当前路径和的差为 targetSum 值。

③ 先序遍历

hash[total]++;
count += helper(root->left, total, targetSum);
count += helper(root->right, total, targetSum);
hash[total]--;

在走向下一个节点之前，先把当前路径和存入 hash 表中，因为它是前缀和。同时，当基于这条路径的所有路径都被遍历完毕后，要把这条路径的路径和移出 hash 表，即 hash[total]-- 。

比如，我们遍历完了节点 “3” 及其左右子树，接下来就该遍历 “5” 的右子树了。而 “5” 的右子树不会经过路径 “10, 5, 3” 。因此，在节点 “3” 发现自己的左右子树被遍历完时，“3” 就应该回收以自己为终点的路径 “10, 5, 3” 了。

class Solution {
public:unordered_map<long, int> hash;int helper(TreeNode * root, long total, int targetSum) {if (!root) return 0;int count = 0;total += root->val;if (hash.count(total - targetSum)) {count = hash[total - targetSum];}hash[total]++;count += helper(root->left, total, targetSum);count += helper(root->right, total, targetSum);hash[total]--;return count;}int pathSum(TreeNode* root, int targetSum) {hash[0] = 1;return helper(root, 0, targetSum);}
};

说明：下述代码是为了处理前缀本身的路径和等于 targetSum 的情况，也就是它（被减数）不需要和另一个前缀（减数）做减法。这里用路径和为 0 来表示减数，否则这种情况会被忽略。