前面的博文中,开发实践过海底相关生物检测识别的项目,对于海洋场景下的海洋生物检测则很少有所涉及,这里本文的主要目的就是想要开发构建基于YOLOv7不同系列参数模型的海洋场景下的海洋生物检测识别系统。
前文已有相关实践,感兴趣的话可以自行移步阅读即可:
《探索海洋世界,基于YOLOv8全系列【n/s/m/l/x】参数模型开发构建海洋场景下海洋生物检测识别分析系统》
《探索海洋世界,基于DETR(DEtection TRansformer)模型开发构建海洋场景下海洋生物检测识别分析系统》
《探索海洋世界,基于YOLOv5全系列【n/s/m/l/x】参数模型开发构建海洋场景下海洋生物检测识别分析系统》
首先看下实例效果:
YOLOv7是 YOLO 系列最新推出的YOLO 结构,在 5 帧/秒到 160 帧/秒范围内,其速度和精度都超过了大部分已知的目标检测器,在 GPU V100 已知的 30 帧/秒以上的实时目标检测器中,YOLOv7 的准确率最高。根据代码运行环境的不同(边缘 GPU、普通 GPU 和云 GPU),YOLOv7 设置了三种基本模型,分别称为 YOLOv7-tiny、YOLOv7和 YOLOv7-W6。相比于 YOLO 系列其他网络 模 型 ,YOLOv7 的 检 测 思 路 与YOLOv4、YOLOv5相似,YOLOv7 网络主要包含了 Input(输入)、Backbone(骨干网络)、Neck(颈部)、Head(头部)这四个部分。首先,图片经过输入部分数据增强等一系列操作进行预处理后,被送入主干网,主干网部分对处理后的图片提取特征;随后,提取到的特征经过 Neck 模块特征融合处理得到大、中、小三种尺寸的特征;最终,融合后的特征被送入检测头,经过检测之后输出得到结果。
YOLOv7 网络模型的主干网部分主要由卷积、E-ELAN 模块、MPConv 模块以及SPPCSPC 模块构建而成 。在 Neck 模块,YOLOv7 与 YOLOv5 网络相同,也采用了传统的 PAFPN 结构。FPN是YoloV7的加强特征提取网络,在主干部分获得的三个有效特征层会在这一部分进行特征融合,特征融合的目的是结合不同尺度的特征信息。在FPN部分,已经获得的有效特征层被用于继续提取特征。在YoloV7里依然使用到了Panet的结构,我们不仅会对特征进行上采样实现特征融合,还会对特征再次进行下采样实现特征融合。Head检测头部分,YOLOv7 选用了表示大、中、小三种目标尺寸的 IDetect 检测头,RepConv模块在训练和推理时结构具有一定的区别。
简单看下实例数据情况:

训练数据配置文件如下所示:
# txt path
train: ./dataset/images/train
val: ./dataset/images/test
test: ./dataset/images/test# number of classes
nc: 4# class names
names: ['tortoise', 'fish', 'coral', 'person']
这里主要是选择了yolov7-tiny、yolov7和yolov7x这三款不同参数量级的模型来进行开发训练,最终线上选取的是yolov7-tiny系列的模型作为推理模型,这里给出来yolov7-tiny的模型文件:
# parameters
nc: 4 # number of classes
depth_multiple: 1.0 # model depth multiple
width_multiple: 1.0 # layer channel multiple# anchors
anchors:- [10,13, 16,30, 33,23] # P3/8- [30,61, 62,45, 59,119] # P4/16- [116,90, 156,198, 373,326] # P5/32# yolov7-tiny backbone
backbone:# [from, number, module, args] c2, k=1, s=1, p=None, g=1, act=True[[-1, 1, Conv, [32, 3, 2, None, 1, nn.LeakyReLU(0.1)]], # 0-P1/2 [-1, 1, Conv, [64, 3, 2, None, 1, nn.LeakyReLU(0.1)]], # 1-P2/4 [-1, 1, Conv, [32, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-2, 1, Conv, [32, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, Conv, [32, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, Conv, [32, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[[-1, -2, -3, -4], 1, Concat, [1]],[-1, 1, Conv, [64, 1, 1, None, 1, nn.LeakyReLU(0.1)]], # 7[-1, 1, MP, []], # 8-P3/8[-1, 1, Conv, [64, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-2, 1, Conv, [64, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, Conv, [64, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, Conv, [64, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[[-1, -2, -3, -4], 1, Concat, [1]],[-1, 1, Conv, [128, 1, 1, None, 1, nn.LeakyReLU(0.1)]], # 14[-1, 1, MP, []], # 15-P4/16[-1, 1, Conv, [128, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-2, 1, Conv, [128, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, Conv, [128, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, Conv, [128, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[[-1, -2, -3, -4], 1, Concat, [1]],[-1, 1, Conv, [256, 1, 1, None, 1, nn.LeakyReLU(0.1)]], # 21[-1, 1, MP, []], # 22-P5/32[-1, 1, Conv, [256, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-2, 1, Conv, [256, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, Conv, [256, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, Conv, [256, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[[-1, -2, -3, -4], 1, Concat, [1]],[-1, 1, Conv, [512, 1, 1, None, 1, nn.LeakyReLU(0.1)]], # 28]# yolov7-tiny head
head:[[-1, 1, Conv, [256, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-2, 1, Conv, [256, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, SP, [5]],[-2, 1, SP, [9]],[-3, 1, SP, [13]],[[-1, -2, -3, -4], 1, Concat, [1]],[-1, 1, Conv, [256, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[[-1, -7], 1, Concat, [1]],[-1, 1, Conv, [256, 1, 1, None, 1, nn.LeakyReLU(0.1)]], # 37[-1, 1, Conv, [128, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, nn.Upsample, [None, 2, 'nearest']],[21, 1, Conv, [128, 1, 1, None, 1, nn.LeakyReLU(0.1)]], # route backbone P4[[-1, -2], 1, Concat, [1]],[-1, 1, Conv, [64, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-2, 1, Conv, [64, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, Conv, [64, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, Conv, [64, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[[-1, -2, -3, -4], 1, Concat, [1]],[-1, 1, Conv, [128, 1, 1, None, 1, nn.LeakyReLU(0.1)]], # 47[-1, 1, Conv, [64, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, nn.Upsample, [None, 2, 'nearest']],[14, 1, Conv, [64, 1, 1, None, 1, nn.LeakyReLU(0.1)]], # route backbone P3[[-1, -2], 1, Concat, [1]],[-1, 1, Conv, [32, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-2, 1, Conv, [32, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, Conv, [32, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, Conv, [32, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[[-1, -2, -3, -4], 1, Concat, [1]],[-1, 1, Conv, [64, 1, 1, None, 1, nn.LeakyReLU(0.1)]], # 57[-1, 1, Conv, [128, 3, 2, None, 1, nn.LeakyReLU(0.1)]],[[-1, 47], 1, Concat, [1]],[-1, 1, Conv, [64, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-2, 1, Conv, [64, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, Conv, [64, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, Conv, [64, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[[-1, -2, -3, -4], 1, Concat, [1]],[-1, 1, Conv, [128, 1, 1, None, 1, nn.LeakyReLU(0.1)]], # 65[-1, 1, Conv, [256, 3, 2, None, 1, nn.LeakyReLU(0.1)]],[[-1, 37], 1, Concat, [1]],[-1, 1, Conv, [128, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-2, 1, Conv, [128, 1, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, Conv, [128, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[-1, 1, Conv, [128, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[[-1, -2, -3, -4], 1, Concat, [1]],[-1, 1, Conv, [256, 1, 1, None, 1, nn.LeakyReLU(0.1)]], # 73[57, 1, Conv, [128, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[65, 1, Conv, [256, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[73, 1, Conv, [512, 3, 1, None, 1, nn.LeakyReLU(0.1)]],[[74,75,76], 1, IDetect, [nc, anchors]], # Detect(P3, P4, P5)]在实验阶段保持完全相同的参数设置,等待全部训练完成之后来从多个指标的维度来进行综合的对比分析。
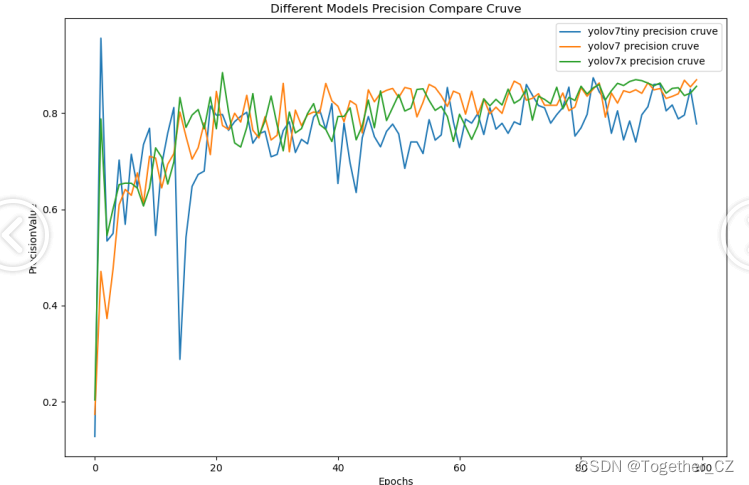
【Precision曲线】
精确率曲线(Precision-Recall Curve)是一种用于评估二分类模型在不同阈值下的精确率性能的可视化工具。它通过绘制不同阈值下的精确率和召回率之间的关系图来帮助我们了解模型在不同阈值下的表现。
精确率(Precision)是指被正确预测为正例的样本数占所有预测为正例的样本数的比例。召回率(Recall)是指被正确预测为正例的样本数占所有实际为正例的样本数的比例。
绘制精确率曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的精确率和召回率。
将每个阈值下的精确率和召回率绘制在同一个图表上,形成精确率曲线。
根据精确率曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
通过观察精确率曲线,我们可以根据需求确定最佳的阈值,以平衡精确率和召回率。较高的精确率意味着较少的误报,而较高的召回率则表示较少的漏报。根据具体的业务需求和成本权衡,可以在曲线上选择合适的操作点或阈值。
精确率曲线通常与召回率曲线(Recall Curve)一起使用,以提供更全面的分类器性能分析,并帮助评估和比较不同模型的性能。
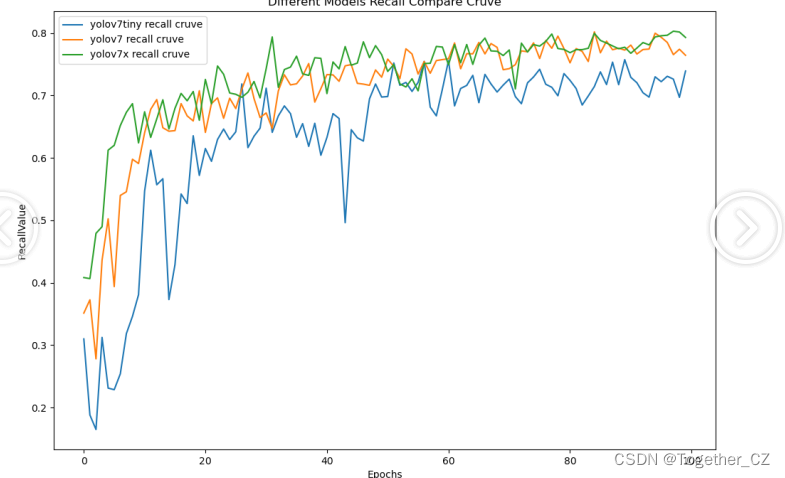
【Recall曲线】
召回率曲线(Recall Curve)是一种用于评估二分类模型在不同阈值下的召回率性能的可视化工具。它通过绘制不同阈值下的召回率和对应的精确率之间的关系图来帮助我们了解模型在不同阈值下的表现。
召回率(Recall)是指被正确预测为正例的样本数占所有实际为正例的样本数的比例。召回率也被称为灵敏度(Sensitivity)或真正例率(True Positive Rate)。
绘制召回率曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的召回率和对应的精确率。
将每个阈值下的召回率和精确率绘制在同一个图表上,形成召回率曲线。
根据召回率曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
通过观察召回率曲线,我们可以根据需求确定最佳的阈值,以平衡召回率和精确率。较高的召回率表示较少的漏报,而较高的精确率意味着较少的误报。根据具体的业务需求和成本权衡,可以在曲线上选择合适的操作点或阈值。
召回率曲线通常与精确率曲线(Precision Curve)一起使用,以提供更全面的分类器性能分析,并帮助评估和比较不同模型的性能。
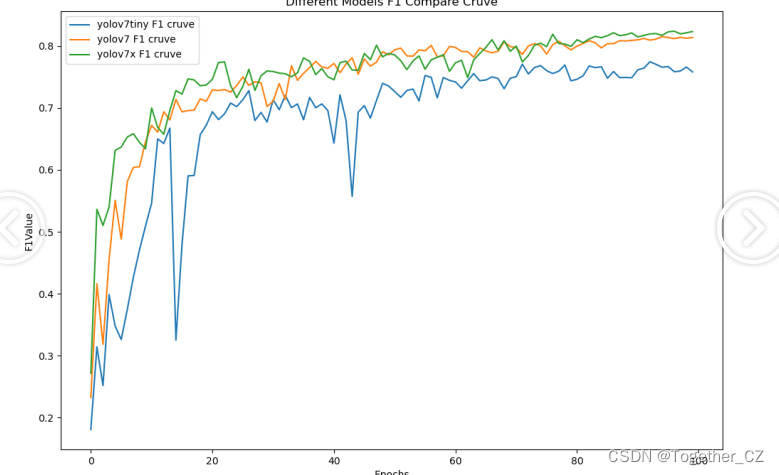
【F1值曲线】
F1值曲线是一种用于评估二分类模型在不同阈值下的性能的可视化工具。它通过绘制不同阈值下的精确率(Precision)、召回率(Recall)和F1分数的关系图来帮助我们理解模型的整体性能。
F1分数是精确率和召回率的调和平均值,它综合考虑了两者的性能指标。F1值曲线可以帮助我们确定在不同精确率和召回率之间找到一个平衡点,以选择最佳的阈值。
绘制F1值曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的精确率、召回率和F1分数。
将每个阈值下的精确率、召回率和F1分数绘制在同一个图表上,形成F1值曲线。
根据F1值曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
F1值曲线通常与接收者操作特征曲线(ROC曲线)一起使用,以帮助评估和比较不同模型的性能。它们提供了更全面的分类器性能分析,可以根据具体应用场景来选择合适的模型和阈值设置。
【loss走势】
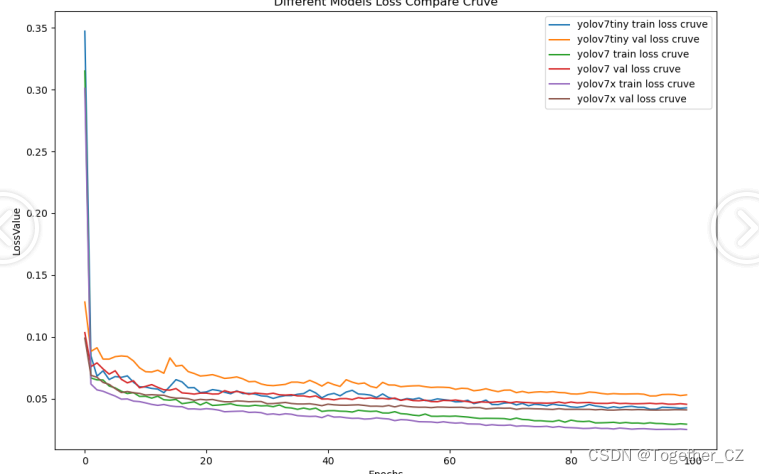
从整体实验对比结果来看:三款不同参数量级的模型最终达到了相近的性能,yolov7x最优,但是tiny系列模型并没有很大的性能差异,考虑到计算量的问题,这里最终选择使用yolov7-tiny来作为最终模型。
接下来我们详细看下yolov7-tiny模型的结果详情。
【Batch实例】


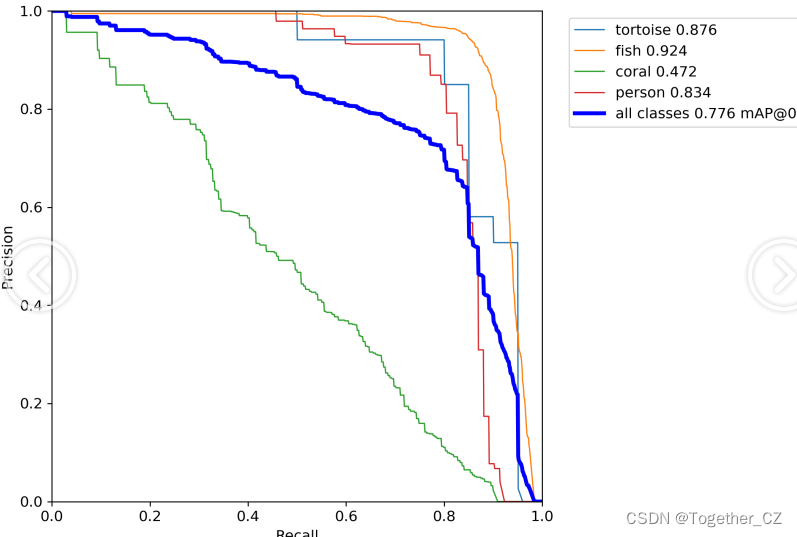
【PR曲线】
【训练可视化】

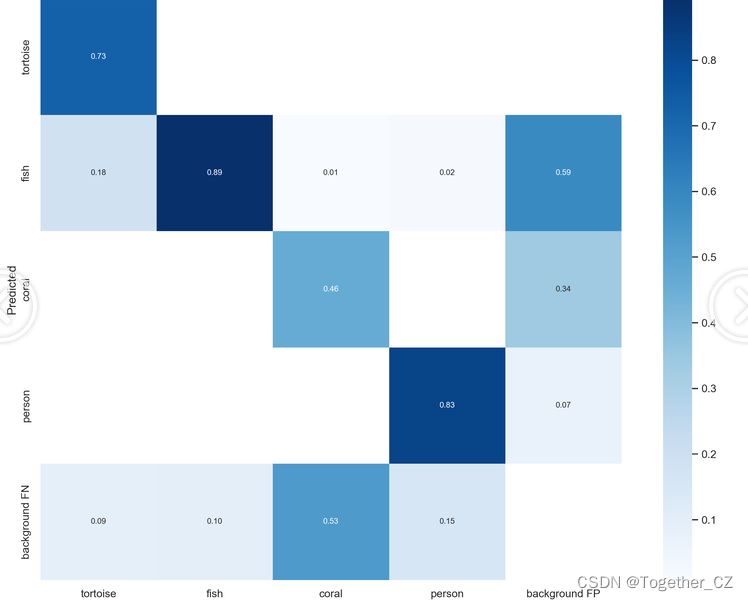
【混淆矩阵】
【离线推理实例】

感兴趣的话都可以自行动手尝试下!
如果自己不具备开发训练的资源条件或者是没有时间自己去训练的话这里我提供出来对应的训练结果可供自行按需索取。
单个模型的训练结果默认YOLOv7-tiny
全系列三个模型的训练结果总集





)











)

