语谱图（一） Spectrogram 的定义与机理

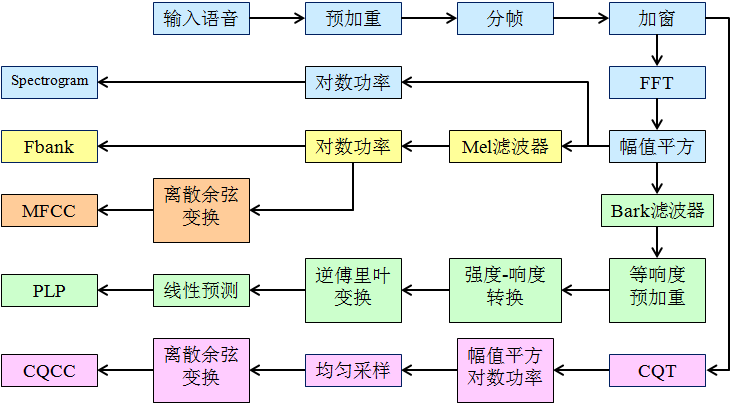
在这里插入图片描述

1. 语谱图 spectrogram

在音频、语音信号处理领域，我们需要将信号转换成对应的语谱图(spectrogram)，将语谱图上的数据作为信号的特征。

语谱图的横坐标是时间，纵坐标是频率，坐标点值为语音数据能量。由于是采用二维平面表达三维信息，所以能量值的大小是通过颜色来表示的，颜色深，表示该点的语音能量越强。

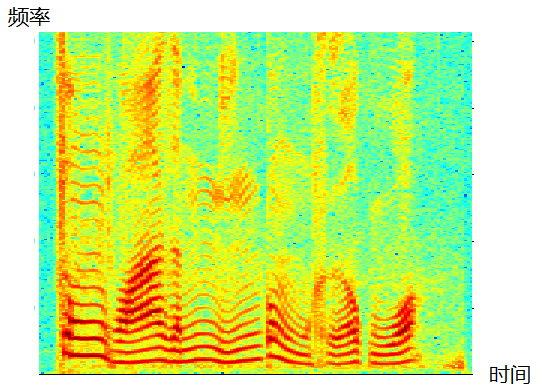
在这里插入图片描述

2. 语谱图形成过程

信号预加重
对信号进行分帧加窗，进行STFT，得到每帧信号的频谱图；
对频谱图进行旋转加映射；
将变换后的多帧频谱进行拼接，形成语谱图；

3. 语谱图的具体实现步骤

3.1 预加重

因为语音信号的功率谱随频率的增加而减小，

导致语音的大部分能量都集中在低频部分，

从而导致高频部分的信噪比很低。
因此一般使用一阶高通滤波器去提升信号在高频部分的信噪比。

对语音进行完预加重后，然后就是分帧加窗操作；

3.2 分帧与加窗

对于一段语音，以10ms~30ms 为一帧，为了保证帧与帧之间平滑过渡保持连续性，帧与帧之间会有重叠。

一段语音信号x(t) , 通过分帧之后，数据由一维信号变为二维信号；

分帧之后，变为x(m,n)
m为帧长，代表每一帧的长度；
n 为帧的个数， n 列代 n个帧；

下图是分帧加窗的示例，这段语音被分为很多帧;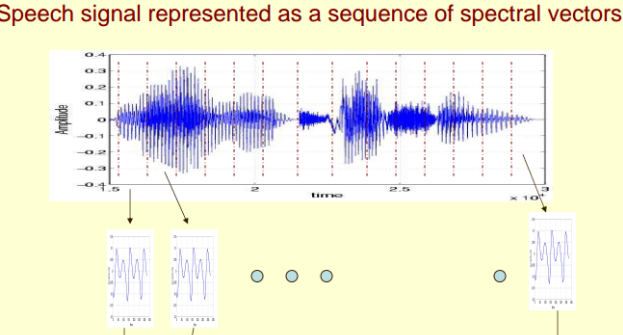 请添加图片描述

3.3 语谱图的形成原理

3.3.1 频谱spectrum 的产生

将每一帧的数据都进行FFT变换（严格来讲，每帧数据加窗后做FFT ，称之为STFT)，由x(m,n) 得到X(m,n)。

X(m,n) 称作频谱，反应了频率与能量之间的关系。

频谱图：
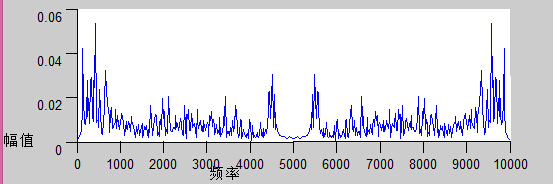
在这里插入图片描述

在实际使用中，频谱图有三种，即

线性振幅谱、
对数振幅谱：（对数振幅谱中各谱线的振幅都作了对数计算，所以其纵坐标的单位是dB分贝）。
自功率谱

这个变换的目的是使那些振幅较低的成分相对高振幅成分得以拉高，以便观察掩盖在低幅噪声中的周期信号。
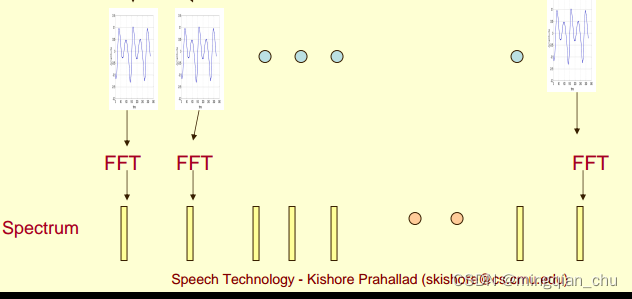
在这里插入图片描述
上图反应了，每帧信号对其做FFT 变换（更具体点，是通过短时FFT计算）。

每帧语音都对应于一个频谱spectrum, 如图中spectrum 所示。

注意：短时傅立叶变换（STFT），返回一个复数矩阵使得D(f,t)
复数的实部：np.abs(D(f,t))频率的振幅
复数的虚部：np.angle(D(f,t))频率的相位

3.3.2 单帧语音的频谱处理

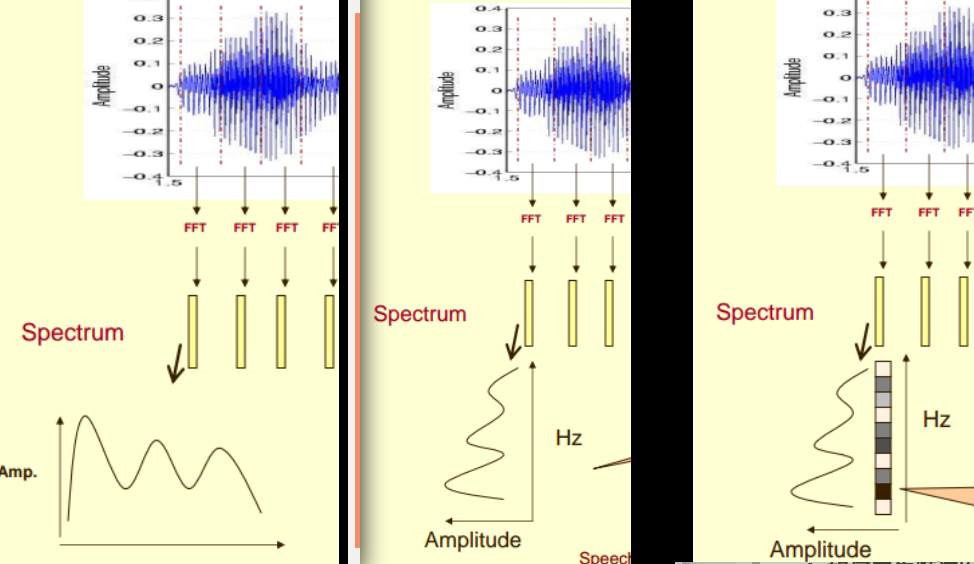
FFT (spectrum) ——> rotated 90 ( spectrum ) ---> project amplitude
我们取出其中一帧语音的频谱，做如下处理：

原始一帧语音的频谱，换一种表达方式，使用坐标表示出来，横轴代表频率，纵轴代表幅度值；
将该坐标轴旋转 90 度，横轴代表幅度值，纵轴代表频率；
对幅度值进行映射，通过量化的方式，0表示白，255表示黑色。幅度值越大，相应的区域越黑，从而去除了幅度值，这个维度，多出一个维度用作表达其他信息；

至此，我们应该明白，对频谱图进行上述操作，
是为了去除了幅度值这个维度，多出一个维度用作表达时间这个维度信息；

3.3.3 对多帧语音的频谱进行拼接

对多帧频谱，重复上述单帧频谱的操作；
将变换后的多帧频谱，在时间维度上，进行拼接，从而形成了多帧信号的语谱图；

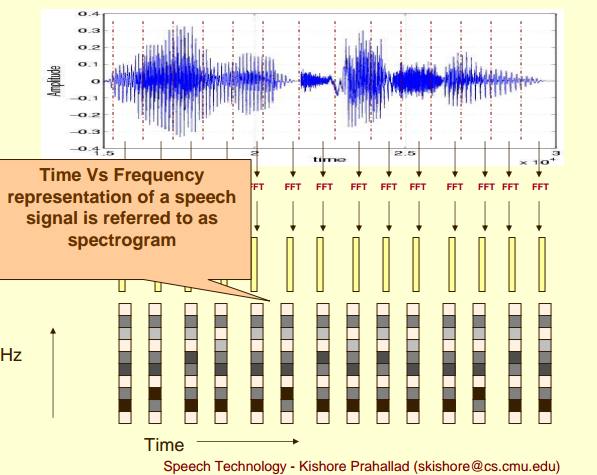
这样就可以显示一段语音而不是一帧语音的功率谱，而且可以直观的看到静态和动态的信息。

3.4 STFT的运行流程

概念——STFT短时傅里叶变换：STFT短时傅里叶变换，实际上是对一系列加窗数据做FFT。有的地方也会提到DCT（离散傅里叶变换），而DCT跟FFT的关系就是：FFT是实现DCT的一种快速算法。
概念——声谱图：对原始信号进行分帧加窗后，可以得到很多帧，对每一帧做FFT（快速傅里叶变换），傅里叶变换的作用是把时域信号转为频域信号，把每一帧FFT后的频域信号（频谱图）在时间上堆叠起来就可以得到声谱图。
FFT有个参数N_fft, 简写为Ｎ，表示对一帧内多少个点做FFT，如果一帧里面的点的个数小于N就会zero-padding到N的长度。每个点对应一个频率区间，频率区间是等间隔，即频率分辨率：　
$freq_{bin} = \frac{F_s}{N_{fft}}$

已知，stft 出来的矩阵是[ 1+ $\frac{N_{fft}}{2}$ , n_frames], 　则纵轴，频率轴的划分为这么多份，小n 属于[1, 1+ $\frac{N_{fft}}{2}$ ]

某一点n（n从1开始）表示的频率为 $F_n=(n−1)∗Fs/N$ ，
第一个点（n=1，Fn等于0）表示直流信号，
纵坐标的中间点，　代表该频率bin 所对应的频率；
最后一个点为 1+ $\frac{N_{fft}}{2}$ ，　代表的是采样频率的一半，即Fs/2。

FFT后我们可以得到N个频点，比如，采样频率为16000，N为1600，那么FFT后就会得到1600个点，FFT得到的1600个值的模可以表示1600个频点对应的振幅。因为FFT具有对称性，当N为偶数时取N/2+1个点，当N为奇数时，取(N+1)/2个点，比如N为512时最后会得到257个值。

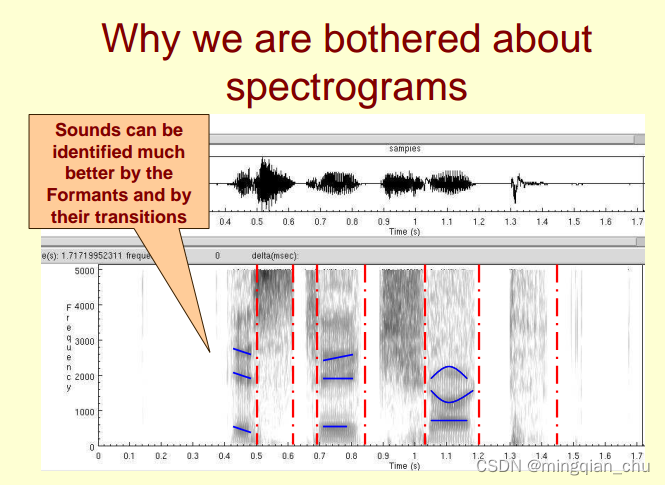
4. 为什么需要语谱图？

因为声谱图中有很多重要的特征，比如音素特征；
共振峰特征（formants 即频谱图中的峰值）
以及观察他们的转变趋势，可以更好的识别音频；

语音信号的时间-频率表示方法：
语谱图是研究语音（音素Phone）的工具
语音学家对音素Phone及其特性进行直观研究
隐马尔科夫模型隐含了语音到文本系统的语谱图模型
有助于评估文本到语音系统——一个高质量的文本到语音系统应该产生合成语音，其频谱图应该与自然句子几乎一致

在这里插入图片描述

5. 频谱与语谱图之间的关系

从上述分析，单帧的信号的频谱可以看出，

语谱图这个概念的出现，是为了弥补频谱图，丢失了时间这个维度的信息，故而增加了时间这个维度。

具体的方式，就是将频谱中的幅度值这个维度替换掉（使用颜色的深度来表示)，从多出了一个维度；

而这个多出的维度，便是留作扩展出，时间这个维度的信息；

所以， 语谱图使用二维的表现形式，涵盖了三个维度的信息
（纵轴：频率，横轴：时间；颜色深度：幅度值大小）

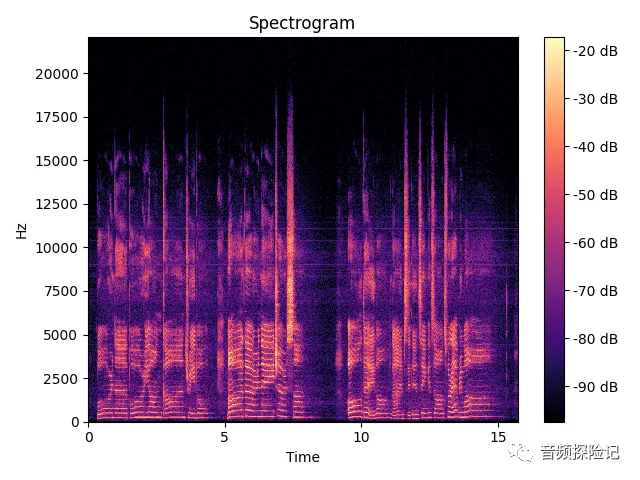
6. 语谱图的coding:

代码实现：

import matplotlib.pyplot as plt
import librosa
import numpy as np
import soundfile as sf
import python_speech_features as psf
import librosa
import librosa.display
# Spectrogram步骤，
# Step 1: 预加重
# Step 2: 分帧
# Step 3: 加窗
# Step 4: FFT
# Step 5: 幅值平方
# Step 6: 对数功率
def preemphasis(signal, coeff=0.95):return np.append(signal[1], signal[1:] - coeff * signal[:-1])def pow_spec(frames, NFFT):complex_spec = np.fft.rfft(frames, NFFT)return 1 / NFFT * np.square(np.abs(complex_spec))
def frame_sig(sig, frame_len, frame_step, win_func):''':param sig: 输入的语音信号:param frame_len: 帧长:param frame_step: 帧移:param win_func: 窗函数:return: array of frames, num_frame * frame_len'''slen = len(sig)if slen <= frame_len:num_frames = 1else:# np.ceil(), 向上取整num_frames = 1 + int(np.ceil((slen - frame_len) / frame_step))padlen = int( (num_frames - 1) * frame_step + frame_len)# 将信号补长，使得(slen - frame_len) /frame_step整除zeros = np.zeros((padlen - slen,))padSig = np.concatenate((sig, zeros))indices = np.tile(np.arange(0, frame_len), (num_frames, 1)) + np.tile(np.arange(0, num_frames*frame_step, frame_step), (frame_len, 1)).Tindices = np.array(indices, dtype=np.int32)frames = padSig[indices]win = np.tile(win_func(frame_len), (num_frames, 1))return frames * winy, sr = sf.read('q1.wav')
# 预加重
y = preemphasis(y, coeff=0.98)
# 分帧加窗
frames = frame_sig(y, frame_len=2048, frame_step=512, win_func=np.hanning)
# FFT及幅值平方
feature = pow_spec(frames, NFFT=2048)
# 对数功率及绘图.
librosa.display.specshow(librosa.power_to_db(feature.T),sr=sr, x_axis='time', y_axis='linear')
plt.title('Spectrogram')
plt.colorbar(format='%+2.0f dB')
plt.tight_layout()
plt.show()