题目链接

F. Greetings

题意

题解

由于两个人的速度是一样的，所以到达终点之前两个人是不会相遇的，考虑一下什么情况两个人会相遇，其中一个人到达终点时，另一个人，终点所在地的前面，并且它的终点在更右边。
将两个人的起点终点分别用$S_a、S_b、E_a、E_b$表示，并假设$a$在前$b$在后（b在前是对称的），有下图

1. $a$的终点$<$ $b$的终点，这时两者同时出发，a到终点时，b已经经过的a的终点，两者不会相遇，对答案没有贡献
   
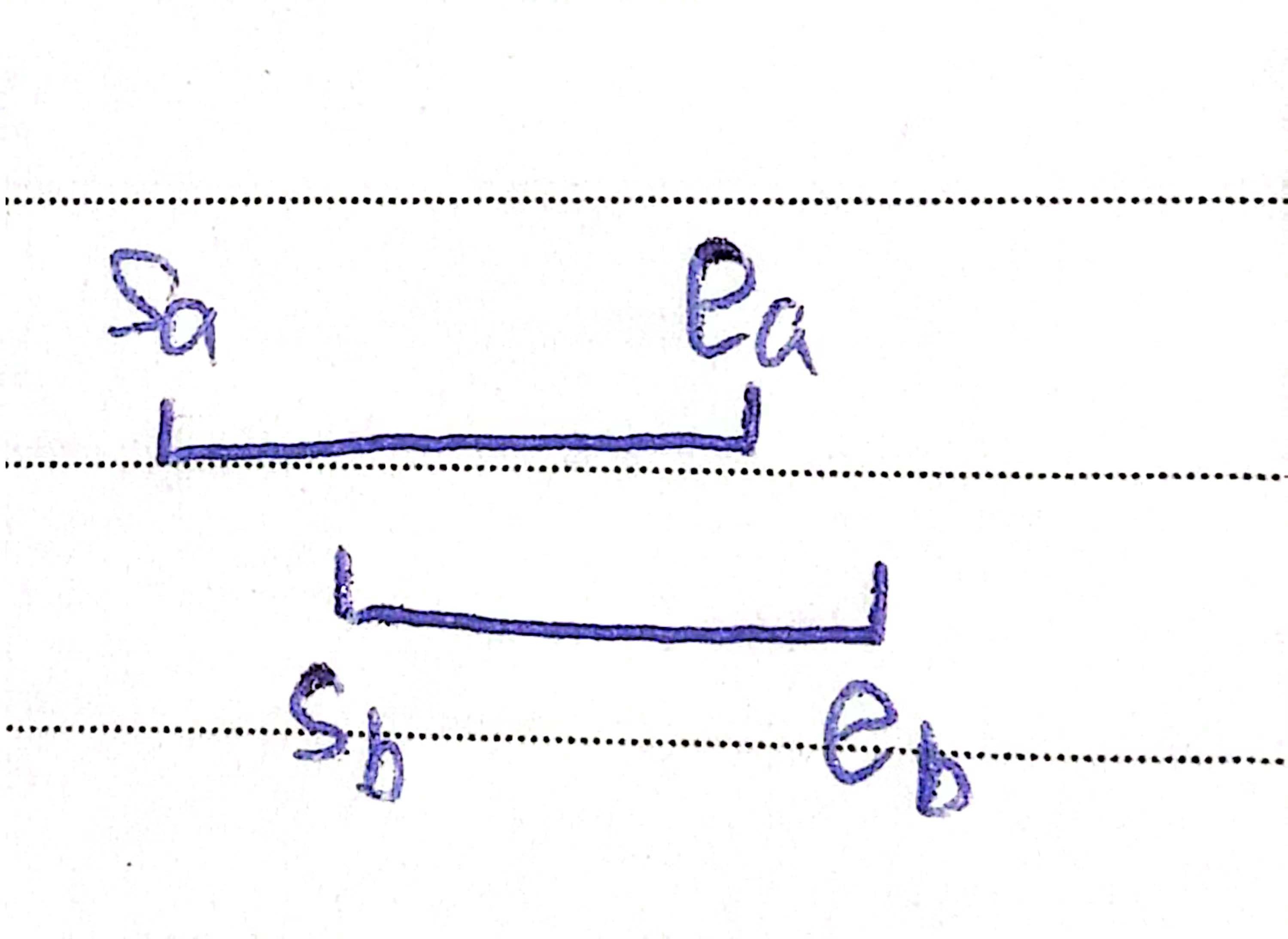
2. $a$的终点$>$ $b$的终点，这时b会先到终点，速度一样，a此时还没有到达$E_b$，此时两者一定会在$E_b$相遇
   
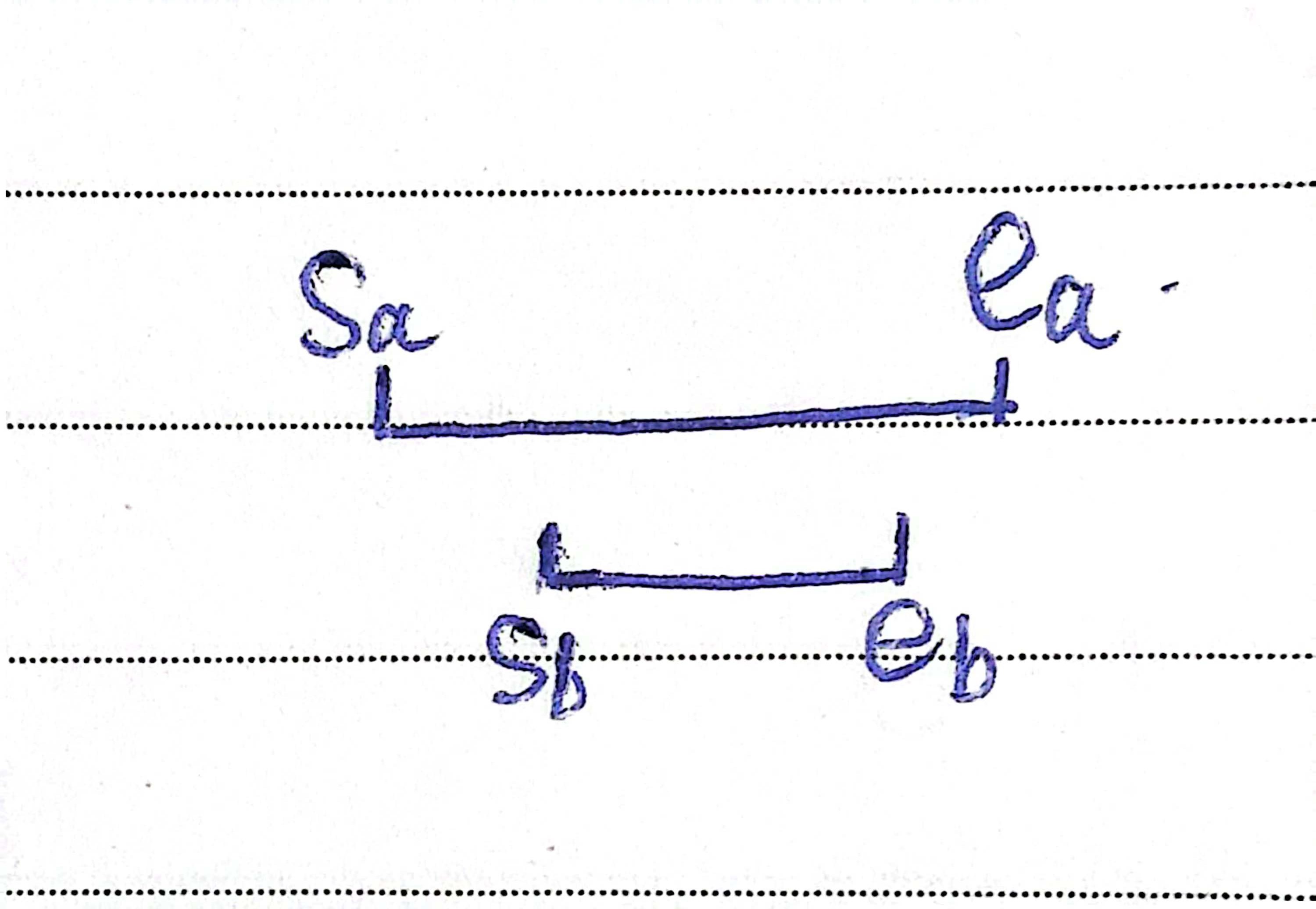
   所以答案转化为对于当前区间计算有多少个区间被它所包含。

因为这道题目数据的实际大小是没有意义的，相对大小是有用的，并且值域比较大，我们考虑离散化，然后通过树状数组去查询。
具体的做法是，先按右端点从小打大排序，然后从前往后遍历区间，每次查询起点大于当前点起点的个数。就是这个区间对答案产生的贡献。

代码

#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_backusing namespace std;void solve() {int n;cin>>n;struct node{int l,r;bool operator<(const node &t)const{return r<t.r;}};vector<node>a(n);vector<int>b(2*n);int k=0;rep(i,0,n-1){cin>>a[i].l>>a[i].r;b[k++]=a[i].l;b[k++]=a[i].r;}sort(b.begin(),b.end());rep(i,0,n-1){a[i].l=lower_bound(b.begin(),b.end(),a[i].l)-b.begin()+1;a[i].r=lower_bound(b.begin(),b.end(),a[i].r)-b.begin()+1;}sort(a.begin(),a.end());
//	rep(i,0,n-1){
//		cout<<a[i].l<<' '<<a[i].r<<endl;
//	}vector<int>c(2*n+1,0);auto lowbit=[](int x){return x&-x;};auto add=[&](int x,int k)->void{for(int i=x;i<=2*n;i+=lowbit(i)){c[i]+=k;}	};auto sum=[&](int x){int res=0;for(int i=x;i;i-=lowbit(i)){res+=c[i];}	return res;};int ans=0;rep(i,0,n-1){int r=a[i].r,l=a[i].l;ans+=sum(r)-sum(l-1);add(l,1);}cout<<ans<<endl;
}signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
//	freopen("1.in", "r", stdin);int _;cin>>_;while(_--)solve();return 0;
}

---

总结

1. 离散化的板子记得不是很熟，这种东西应该很熟并且默写的很快的
2. 树状数组用的还是比较少有些细节记得不太清，就比如树状数组的下标是从几开始的？
   答案是1，这就导致离散化的时候也要从1开始。
3. 看了一些题解，发现了这类问题被称为二维偏序问题
   $a_i<a_j、b_i>b_j$

---