比赛链接

这场打的很顺，感觉难度和 div 4 差不多，不是很难。D题稍微考了考同余的性质，E题直接模拟过程即可，F题也可以暴力模拟或者拓扑排序，G题是个数学题，是个简单隔板法。A到F题都可以直接模拟就有点离谱。

---

A. Recovering a Small String

题意：

尼基塔的单词正好由 $3$ 个小写拉丁字母组成。拉丁字母的编号从 $1$ 到 $26$ ，其中字母 "a "的编号为 $1$ ，字母 "z "的编号为 $26$ 。

他将这个单词编码为字母表中所有字符的位置总和。例如，他将单词 "cat "编码为整数 $3+1+20=24$ ，因为字母 "c "在字母表中的索引为 $3$ ，字母 "a "的索引为 $1$ ，字母 "t "的索引为 $20$ 。

然而，这种编码结果是模糊的！例如，对单词 "ava "进行编码时，也会得到整数 $1+22+1=24$ 。

请找出由 $3$ 个字母组成的字典序最小的单词。

当且仅当以下条件之一成立时，字符串 $a$ 在词法上小于字符串 $b$ ：

• $a$ 是 $b$ 的前缀，但 $a\ne b$ ；
• 在 $a$ 和 $b$ 不同的第一个位置，字符串 $a$ 的字母在字母表中出现的时间早于 $b$ 中的相应字母。

思路：

显然先动后面的字母，大的字母放在后面。初始是aaa，先第三个位置上从a到z，这时 $n\in [3,28]$，然后第二个位置从a到z，这时 $n\in [29,53]$，最后第一个位置从a到z，这时 $n\in [54,78]$。

也可以直接dfs爆搜，毕竟就三个位置。

code：

#include <iostream>
#include <cstdio>
using namespace std;int T,n;int main(){cin>>T;while(T--){cin>>n;if(n<=28)printf("aa%c\n",n-2-1+'a');else if(n<=53)printf("a%cz\n",n-1-26-1+'a');else printf("%czz\n",n-26-26-1+'a');}return 0;
}

---

B. Make Equal

题意：

有 $n$ 个盛水的容器一字排开，从左到右依次编号为 $1$ 到 $n$ 。每个容器可以装任意数量的水；最初，第 $i$ 个容器装有 $a_i$ 个单位的水。 $a_i$ 的和能被 $n$ 整除。

你可以任意(可能是零)次地执行下面的操作：从第 $i$ 个容器中倒入任意数量的水到第 $j$ 个容器中，其中 $i$ 必须小于 $j$ (即 $i<j$ )。任何下标都可以被选择为 $i$ 或 $j$ ，次数不限。

请判断是否有可能通过这种操作使所有容器中的水量相同。

思路：

可以任意选择两个位置，并把前面的位置的容器的水向后倒任意数量的水，所以只要前面的容器水量够用，就可以倒给后面的容器，使得它们的水量相同。反之就没有办法相同。

换句话说，假设平均水量为 $ave$，如果前 $i-1$ 个位置的总水量大于等于 $ave\ast (i-1)$，那么前 $i-1$ 个位置就可以向第 $i$ 个位置贡献水量，还得有足够的水量把它变成 $ave$ 水量，这样前 $i$ 个位置的总水量大于等于 $ave\ast i$。否则第 $i$ 个位置永远不可能达到平均水量。所以直接枚举每一个 $i$ 看看它的前缀和水量是否超过了 $ave\ast i$，否则就会导致某个位置达不到平均水量。

code：

#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=2e5+5;
typedef long long ll;int T,n,a[maxn];int main(){cin>>T;while(T--){cin>>n;ll tot=0,ave;for(int i=1;i<=n;i++){cin>>a[i];tot+=a[i];}ave=tot/n;ll res=0;bool f=true;for(int i=1;i<=n;i++){res+=a[i];if(res<ave*i){f=false;break;}}puts((f)?"YES":"NO");}return 0;
}

---

C. Make Equal Again

题意：

你有一个由 $n$ 个整数组成的数组 $a$ 。

您可以至多一次进行以下操作：选择三个整数 $i$ , $j$ , $x$ ( $1\le i\le j\le n$ )，并将数组中索引为 $i$ 至 $j$ 的所有元素赋值为 $x$ 。这个操作的代价取决于所选的索引，等于 $(j-i+1)$ 。

例如，数组等于 $[1,2,3,4,5,1]$ 。如果我们选择 $i=2,j=4,x=8$ ，那么执行此操作后，数组将等于 $[1,8,8,8,5,1]$ 。

要使数组中的所有元素相等，最少需要花费多少布尔值？

思路：

因为只能进行一次操作，还要让所有元素相同，那么就要把中间所有不同的数字全部换掉。具体来说，最左边和最右边可能有两种数字，考虑把从左边第一个不同的数字开始把后面换成最左边的数字，以及把从右边第一个不同的数字开始把前面换成最右边的数字，两种情况都算一遍然后取最小值即可。特殊情况就是左右两边数字相同，这时只换掉中间的数即可。

code：

#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=2e5+5;int T,n,a[maxn];int main(){cin>>T;while(T--){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];int l=1,r=n,ans=1145141919;while(l<n && a[l+1]==a[l])l++;while(r>1 && a[r-1]==a[r])r--;if(a[1]==a[n])ans=(r>l)?r-l-1:0;else ans=min(n-l,r-1);cout<<ans<<endl;}return 0;
}

---

D. Divisible Pairs

题意：

波利卡普有两个最喜欢的整数 $x$ 和 $y$ (它们可以相等)，他找到了一个长度为 $n$ 的数组 $a$ 。

如果出现以下情况，波利卡普认为一对索引 $⟨i,j⟩$ ( $1\le i<j\le n$ ) 很美：

• $a_i+a_j$ 可以被 $x$ 整除；
• $a_i-a_j$ 能被 $y$ 整除。

例如，如果 $x=5$ , $y=2$ , $n=6$ , $a=$ [ $1,2,7,4,9,6$ ]，那么唯一美丽的一对是：

• $⟨1,5⟩$ : $a_1+a_5=1+9=10$ $10$ 能被 $5$ 整除）和 $a_1-a_5=1-9=-8$ ( $-8$ 能被 $2$ 整除）；
• $⟨4,6⟩$ : $a_4+a_6=4+6=10$ $10$ 能被 $5$ 整除）和 $a_4-a_6=4-6=-2$ ( $-2$ 能被 $2$ 整除)。

求数组 $a$ 中优美对的个数。

思路：

同余的性质，相加能被x整除，那么先同余x再相加同样能被x整除，相减被y整除，那么先同余y再相减同样能被y整除（其实相当于就是两者余数相同）

所以对一个数，它同余x和同余y的余数其实已经确定了，其实就是找和它配成同余x的余数相加能被x整除以及同余y的余数相同的数前面有多少个。因为xy同样可以很大，开桶会爆空间，所以使用map或者set。

考虑使用map<pair<int,int>,int> ，前面的pair键描述分别同余x和y的余数信息，后面的int值记录数量即可。

code：

#include <iostream>
#include <cstdio>
#include <map>
using namespace std;int T,n,x,y;int main(){cin>>T;while(T--){cin>>n>>x>>y;map<pair<int,int>,int> mp;//同余x y的信息，个数 long long ans=0;for(int i=1,t;i<=n;i++){cin>>t;ans+=mp[make_pair((x-t%x)%x,t%y)];mp[make_pair(t%x,t%y)]++;}cout<<ans<<endl;}return 0;
}

---

E. Anna and the Valentine’s Day Gift

题意：

情人节那天，萨沙给了安娜一张 $n$ 个整数的列表 $a$。安娜不需要这个列表，所以她建议通过玩游戏来销毁它。

玩家轮流玩。萨沙是个绅士，所以他让安娜先下手为强。

• 轮到安娜时，她必须从列表中选择一个元素 $a_i$ ，并颠倒其数字顺序。例如，如果安娜选择了数值为 $42$ 的元素，它就会变成 $24$ ；如果安娜选择了数值为 $1580$ 的元素，它就会变成 $851$ 。注意，前导零会被去掉。在这一轮之后，列表中元素的数量不会改变。
• 轮到萨沙时，他必须从列表中提取两个元素 $a_i$ 和 $a_j$ ( $i\ne j$ )，以任意顺序将它们连接起来，并将结果插回列表。例如，如果萨沙选择了等于 $2007$ 和 $19$ 的元素，他将从列表中删除这两个元素，并添加整数 $200719$ 或 $192007$ 。这样转一圈后，列表中的元素数会减少 $1$ 。

玩家不能跳过回合。当列表中只剩下一个整数时，游戏结束。如果这个整数不小于 $10^m$ (即 $\ge 10^m$ )，萨沙获胜。否则，安娜获胜。

由此可以看出，游戏总会结束。如果双方都以最佳方式下棋，谁会获胜？

思路：

模拟一下游玩过程很快就会发现，其实我们对这个数具体是什么根本不关心，Anna只关心能不能利用去除前导零的规则削减数位，Sasha只关心能不能利用合并规则来保护后导零不被变成前导零（要保护的数放在任意一个数前面即可）。因为 $10^m$ 是 $m+1$ 位数中最小的那个数，所以只要你最后合并出来的数数位个数大于等于 $m+1$，那么这个数就一定大于等于 $10^m$，不需要关心具体合并出来一个什么东西。

模拟游玩过程，一开始Anna一定会取出当前 后导零最多的数，将它翻转，这时总的数位会损失后导零个数个数位（因为所有数都不为0，所以不用考虑0这种特殊情况）。然后Sasha会取出当前 后导零最多的数，将它保护起来，这时这个数的后导零就消失了，总位数就会累加到答案里，同理后面的步骤。

所以可以直接暴力模拟这个过程。使用set<pair<int,int> >来存储一个数，前一位表示后导零位数，后一位表示这个数的位数。每次先取出当前后导零数位个数最大的数，后导零位数归零，位数减去损失的位数，放回，然后再取出当前后导零数位个数最大的数，直接将位数加入到答案即可。不过要注意的是，数是可以重复的，后导零位数和这个数的位数是有可能重复的，但是set不能存储重复信息，所以可以多加一维，用来存储没啥特殊含义的数，用来区分它们。

code：

#include <iostream>
#include <cstdio>
#include <set>
using namespace std;int T,n,m;pair<int,int> g(int x){//后导0 总位数 int cnt1=0,cnt2;while(x%10==0){cnt1++;x/=10;}cnt2=cnt1;while(x){cnt2++;x/=10;}return make_pair(cnt1,cnt2);
}int main(){cin>>T;while(T--){cin>>n>>m;set<pair<pair<int,int>,int> > S;for(int i=1,t;i<=n;i++){cin>>t;S.insert(make_pair(g(t),i));}int ans=0;while(!S.empty()){pair<pair<int,int>,int> x=*S.rbegin();S.erase(x);x.first.second-=x.first.first;x.first.first=0;S.insert(x);x=*S.rbegin();S.erase(x);ans+=x.first.second;}puts((ans>m)?"Sasha":"Anna");}return 0;
}

其实这么写还是比较差强人意的，太麻烦了。考虑到一个数后导零被删掉之后总位数就不会再变化了，之后Anna选不选其实无所谓，Anna能消除的只有后导零位数最大的，第三大的，第五大的…所以我们记录一下总位数，然后把所有后导零位数拿出来排个序，奇数位上的后导零位数可以被Anna消除掉，就在总位数上减掉这一部分，剩下的就是答案数字的位数。

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn=2e5+5;int T,n,m,a[maxn];pair<int,int> g(int x){int cnt1=0,cnt2;while(x%10==0){cnt1++;x/=10;}cnt2=cnt1;while(x){cnt2++;x/=10;}return make_pair(cnt1,cnt2);
}int main(){cin>>T;while(T--){cin>>n>>m;int ans=0;for(int i=1,t;i<=n;i++){cin>>t;pair<int,int> tmp(g(t));a[i]=tmp.first;ans+=tmp.second;}sort(a+1,a+n+1,greater<int>());for(int i=1;i<=n;i+=2)ans-=a[i];puts((ans>m)?"Sasha":"Anna");}return 0;
}

---

F. Chat Screenshots

题意：

编程竞赛聊天室有 $n$ 人。聊天参与者按活动排序，但每个人都把自己排在最前面。

例如，有 $4$ 人参加聊天，他们的顺序是 $[2,3,1,4]$ 。那么

• 第 $1$ 个用户看到的顺序是 $[1,2,3,4]$ 。
• 第 $2$ 个用户看到的顺序是 $[2,3,1,4]$ 。
• 第 $3$ 个用户看到的顺序是 $[3,2,1,4]$ 。
• 第 $4$ 个用户看到的顺序是 $[4,2,3,1]$ 。

$k$ 人在聊天中发布了截图，显示了该用户看到的参与者顺序。这些截图是在很短的时间内截取的，参与者的顺序并没有改变。

你的任务是确定所有截图是否都有一定的顺序。

思路1：

这题可以直接模拟，也可以拓扑排序，用拓扑排序很好写，甚至还看到用树状数组的。

题目上非常好心的保证了 每个截图都是一个排列，而且 $k$ 个截图的开头的数字各不相同

而且手玩一下数据的话其实不难发现一般只要两组截图就可以推理出来原序列。具体来说，如果两个截图表示的原序列是一致的，那么就会出现下面这种情况（以题目第三组样例举例）：

两个序列从 $2\sim n$ 第一个出现不同的位置 $i$ 上 其中一个序列上的数一定是另一个序列的开头数字。这时这个序列第 $i$ 个位置就填补上了另一个序列的漏洞，这个序列第 $2\sim i$ 和另一个序列 $i\sim n$ 组合起来就是原序列。

不过想法很美好，但是会出现特例。当这两个数在原序列中紧挨在一起时，就没有办法区分了，比如第九个样例前两个序列：

3 5 1 4 2
2 5 1 4 3

这时候可以推出来两种可行的情况：

5 1 4 3 2
5 1 4 2 3

不过也就仅此而已了，出现这种特例的原因是两者紧挨，导致另一个数被提取到前方时两者中间没有标识前后位置的数。实际上可以直接特判这种情况，然后两种情况都验证一遍。出现这种情况时，两个序列从 $2\sim n$ 第一个出现不同的位置 $i$ 上 其中一个序列上的数一定是另一个序列的开头数字，反过来，另一个序列上的数也一定是这个序列的开头数字。

找到原序列后就可以对 $k$ 个截图进行一一验证，前两个用来构造的截图也要验证，因为不能保证前两个截图的原序列是相同的，这时候构造出来的原序列是有问题的，不过没有关系，在验证前两个序列的时候一定会出错。

$n\ast k\le 2\ast 10^5$，但是 $n,k\le 2\ast 10^5$，所以需要动态开空间。

code1：

#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
const int maxn=2e5+5;int T,n,k;
int t[maxn],t1[maxn];int main(){cin>>T;while(T--){cin>>n>>k;vector<vector<int> > a(k+1,vector<int>(n+1));for(int i=1;i<=k;i++)for(int j=1;j<=n;j++)cin>>a[i][j];if(k==1){puts("YES");continue;}bool f=true,flag=false;for(int i=2;i<=n;i++){if(a[1][i]!=a[2][i]){if(a[1][i]==a[2][1]){if(a[2][i]==a[1][1]){flag=true;for(int j=2;j<=i;j++)t1[j-1]=a[2][j];for(int j=i;j<=n;j++)t1[j]=a[1][j];}for(int j=2;j<=i;j++)t[j-1]=a[1][j];for(int j=i;j<=n;j++)t[j]=a[2][j];}else if(a[2][i]==a[1][1]){for(int j=2;j<=i;j++)t[j-1]=a[2][j];for(int j=i;j<=n;j++)t[j]=a[1][j];}else {f=false;}break;}}if(!f){puts("NO");continue;}int idx;for(int i=1;i<=k;i++){idx=1;for(int j=2;j<=n;j++){if(a[i][1]==t[idx])idx++;if(a[i][j]==t[idx])idx++;else f=false;}}if(!f && flag){//打复活赛 
//			cout<<"想你了牢大"<<endl;f=true;for(int i=1;i<=k;i++){idx=1;for(int j=2;j<=n;j++){if(a[i][1]==t1[idx])idx++;if(a[i][j]==t1[idx])idx++;else f=false;}}}puts((f)?"YES":"NO");}return 0;
}

思路2：

由于每一个截图相当于确定了 $2\sim n$ 位置上的 $n-1$ 个数的相对位置，这个相对位置是不会变化的，比如前面有个截图说2在3前面，这时如果后面有个截图说3在2前面，这时候肯定就矛盾了，所以2在3前面的事实就固定了，是一个拓扑序，所以可以使用拓扑排列。如果没法拓扑排列，说明成环了，这时就会出现矛盾。

或者换种思路，原本的顺序应该是一个从前到后的链一样的关系，所有的截图都满足这个顺序，所以应当是没有环的。如果有一个截图遵循另一个顺序，就会导致至少有一对数发生了交换，这时候从i到j的路径就会以从j到i的路径出现，也就是成环了。这个东西就可以拓扑排序来做。

code2：

#include <iostream>
#include <cstdio>
#include <queue>
using namespace std;
const int maxn=2e5+5;int T,n,k;int head[maxn],d[maxn],cnt;
struct edge{int v,nxt;
}e[maxn<<1];
void add(int u,int v){d[v]++;e[++cnt].v=v;e[cnt].nxt=head[u];head[u]=cnt;
}int main(){cin>>T;while(T--){cin>>n>>k;for(int i=1;i<=n;i++)head[i]=d[i]=0;cnt=0;for(int i=1,u,v;i<=k;i++){for(int j=1;j<=n;j++){cin>>v;if(j>2)add(u,v);u=v;}}queue<int> q;int counter=0;for(int i=1;i<=n;i++)if(!d[i]){q.push(i);counter++;}while(!q.empty()){int u=q.front();q.pop();for(int i=head[u],v;i;i=e[i].nxt){v=e[i].v;d[v]--;if(!d[v]){q.push(v);counter++;}}}puts((counter==n)?"YES":"NO");}return 0;
}

思路3：

无意之间翻到的一个解法，也挺有意思的。

如果我们对第一个序列的 $2\sim n$ 上的数重新编号，其实后面的验证相当于看有没有逆序对，如果出现逆序对就错了。另外我们还要第一个序列开头数字的可能位置并进行验证，可以在验证后面的截图时看后面第一个序列开头数字的位置来找到它在第几个数和第几个数之间，如果多个截图冲突了，就说明无解。

其实树状数组实现的功能就是找逆序对。

code3：

某个大佬的解法

---

G. One-Dimensional Puzzle

题意：

您有一个一维拼图，所有拼图都需要排成一行，并相互连接。所有拼图元素都是完全白色的，只有当它们的形状不同时才能相互区分。

每个元素的顶部和底部都有直线边框，左右两侧都有连接点，每个连接点都可以是一个突出物或一个凹槽。不能旋转拼图。

可以看出，拼图的类型正好有 $4$ 种。如果左边元素的右边连接点与右边元素的左边连接点相对，那么两个元素就可以连接起来。

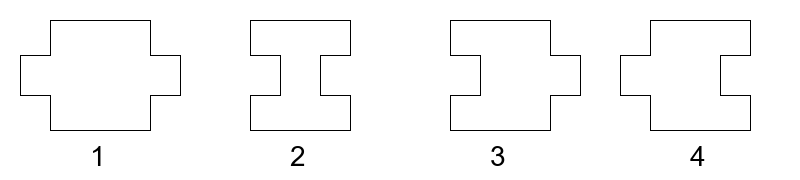所有可能的拼图类型。

谜题中每种类型包含 $c_1,c_2,c_3,c_4$ 个元素。如果您成功地将所有拼图组合成一条长链，那么谜题就算完成了。您想知道有多少种方法可以做到这一点。

思路：

开始之前 先讲隔板法吧。隔板法其实有两种隔板法，一种是解决 不同盒相同球不能空盒 的组合问题，一种是解决 不同盒相同球能空盒 的组合问题（这里相同表示互不区分）。

如果我们要把 $n$ 个相同的球放入到 $m$ 个相同的盒子中，不能空盒，那么可以先把球一字排开，$n$ 个球之间有 $n-1$ 个空隙，我们选取其中的 $m-1$ 个位置放入隔板，这时 $m-1$ 个隔板就将 $n$ 个球分成了 $m$ 段不为空的区间，我们按顺序把每个区间的球放入盒子即可。答案就是 $C_{n-1}^{m-1}=C_{n-1}^{n-m}$。

如果我们要把 $n$ 个相同的球放入到 $m$ 个相同的盒子中，能空盒，那么可以先留出 $n+m-1$ 个位置，先在这 $n+m-1$ 个位置放入 $m-1$ 个隔板，然后把球以此放入空位置上，这时 $m-1$ 个隔板就将 $n$ 个球分成了 $m$ 段可空的区间，我们按顺序把每个区间的球放入盒子即可。答案就是 $C_{n+m-1}^{m-1}=C_{n+m-1}^n$。

上面两种情形的区别只有能不能空盒，实际上，这两种问题是可以相互转化的。对n个相同球，m个不同盒，能空盒的一种合法情况中，可以给每一个盒子里放入一个球，这样问题就转化成了n+m个相同球，m个不同盒，不能空盒的一种合法情况。相反，对n个相同球，m个不同盒，不能空盒的一种合法情况中，可以给每一个盒子里拿出一个球，这样问题就转化成了n-m个相同球，m个不同盒，不能空盒的一种合法情况。这两种情况是一一映射的，方法数是相同的。如果你把 $n=n+m$ 代入到不能空盒的答案 $C_{n-1}^{m-1}$ 中，就会得到 $C_{n+m-1}^{m-1}$，正好就是下面能空盒的答案。

–分割线–

然后回到这个题，发现34号拼图是比较万金油的拼图，如果前面是突起，那么我们就可以在后面接上任意个3号拼图，最后面仍然保持突起，同理4号拼图。

那么我们先不管3和4，只看1和2，发现只能是1和2交替相接，然后1 2之间可以插入3，2 1之间可以插入4。这样的话，1和2的个数最多只能相差1。如果12个数相差为1，那么多的那个放在奇数位上，少的那个放在偶数位上。如果两者数量相同，那么谁放奇数位谁放偶数位都可以，这时有两种方案。不管怎么说，如果只有1 2的话，摆放方案都是固定的。

如果有3 4的话，3可以放在任意的1 2之间的空隙，可以放任意个，如果把1 2之间的空隙看做一个盒子，3看做球，那么就转化成了上面说的 不同盒相同球能空盒 的组合问题了，直接隔板法可以算。两头可以看做是多接了一个虚拟的1或2，这个空隙也要算。比如1 2，他可以看做是2 1 2 1，前面有个虚拟的2，后面有个虚拟的1，这样就有两个2 1空隙，一个1 2空隙。

不过相同的时候有个特殊情况，那就是 $c_1=c_2=0$ 的时候，这时候需要特判。

code：

#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+5;int T,c1,c2,c3,c4;
ll fac[maxn<<1];ll qpow(ll a,ll b){ll base=a,ans=1;while(b){if(b&1){ans*=base;ans%=mod;}base*=base;base%=mod;b>>=1;}return ans;
}
ll inv(ll x){return qpow(x,mod-2);
}
ll C(ll a,ll b){//C_a^breturn fac[a]*inv(fac[b])%mod*inv(fac[a-b])%mod;
}int main(){fac[0]=fac[1]=1;for(int i=2;i<(maxn<<1);i++)fac[i]=fac[i-1]*i%mod;cin>>T;while(T--){cin>>c1>>c2>>c3>>c4;if(abs(c1-c2)>1){cout<<0<<endl;continue;}int a1,a2;//1 2和2 1if(abs(c1-c2)==1){a1=a2=(c1+c2+1)>>1;cout<<(C(a1+c3-1,c3)*C(a2+c4-1,c4)%mod)<<endl;}else {if(c1==0 && c2==0){if(c3 && c4){cout<<0<<endl;continue;}else {cout<<1<<endl;continue;}}a1=c1;a2=a1+1;cout<<(C(a1+c3-1,c3)*C(a2+c4-1,c4)+C(a2+c3-1,c3)*C(a1+c4-1,c4))%mod<<endl;}}return 0;
}