文章目录
- 买卖股票
- 思路一:贪心
- 代码:
- 思路:动态规划
- 代码:
- 跳跃游戏
- 思路:贪心找最大范围
- 代码:
- 跳跃游戏②
- 思路:
- 代码:
- 方法二:处理方法一的特殊情况
买卖股票

思路一:贪心



代码:
// 贪心思路
class Solution {public int maxProfit(int[] prices) {int result = 0;for (int i = 1; i < prices.length; i++) {//如果为正result += Math.max(prices[i] - prices[i - 1], 0);}return result;}
//或者
class Solution {public int maxProfit(int[] prices) {int res=0;for(int i=1;i<prices.length;i++){//如果递增if(prices[i]>prices[i-1]){res+=prices[i]-prices[i-1];}}return res;}
}
思路:动态规划

代码:
class Solution {public int maxProfit(int[] prices) {int[][] dp=new int[prices.length][2];dp[0][0]=-prices[0];dp[0][1]=0;for (int i = 1; i < prices.length; i++) {dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]-prices[i]);dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]+prices[i]);}return Math.max(dp[prices.length-1][0],dp[prices.length-1][1]);}
}
跳跃游戏

思路:贪心找最大范围

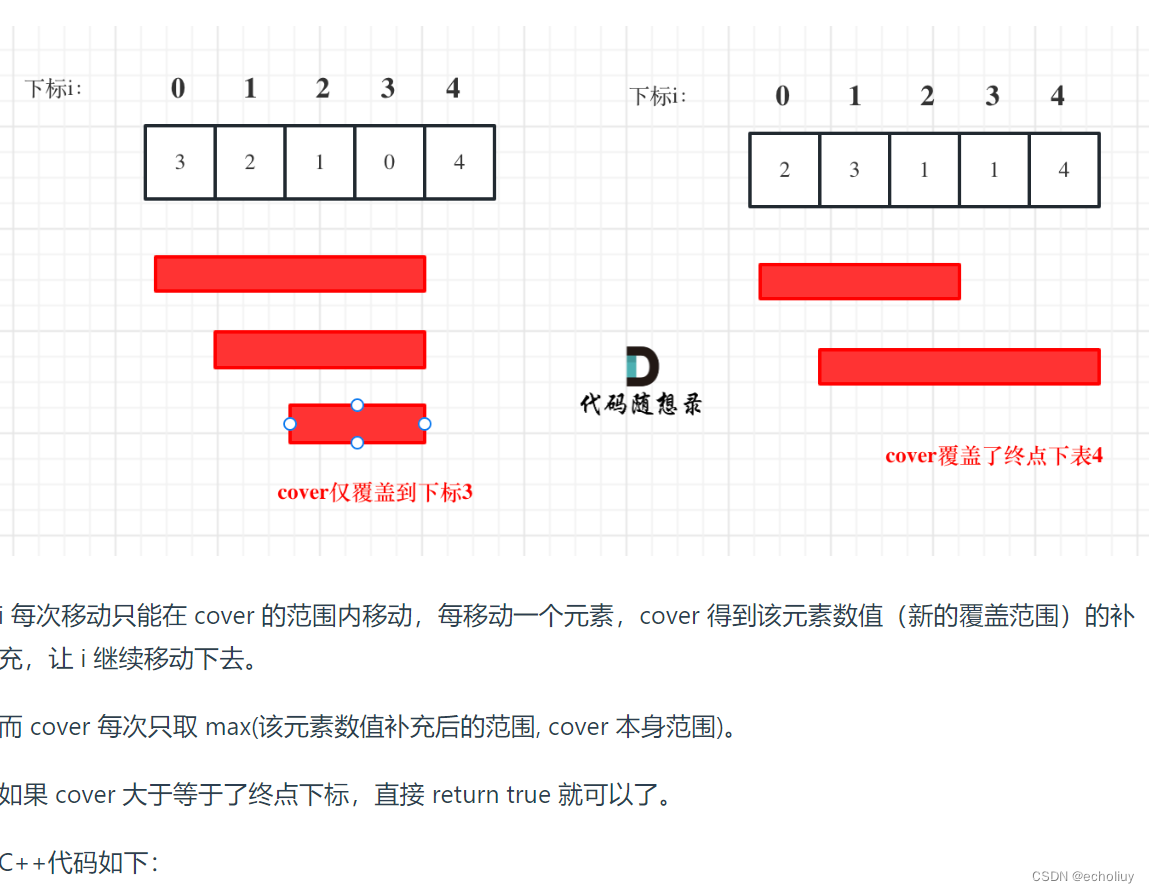
代码:
class Solution {public boolean canJump(int[] nums) {if (nums.length == 1) {return true;}//覆盖范围, 初始覆盖范围应该是0,因为下面的迭代是从下标0开始的int cover=0;//在覆盖范围内更新最大的覆盖范围for(int i=0;i<=cover;i++){cover=Math.max(cover,i+nums[i]);//cover:当前步数覆盖范围 i+nums[i]扩展范围if(cover>=nums.length-1)return true;}return false;}
}
跳跃游戏②

思路:

记录这一步的最大覆盖范围,在这个覆盖范围里,去找里面包含的(下一步能达到的最大覆盖范围)。按照最大覆盖范围去跳,次数就会最少。
每找到一次覆盖范围则相当于跳跃了一次
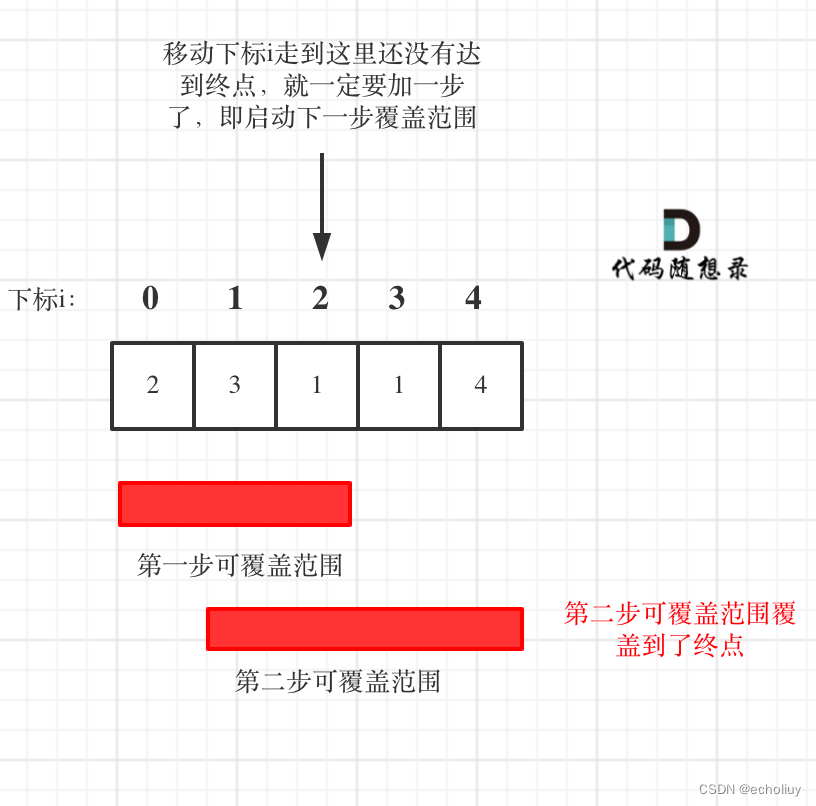
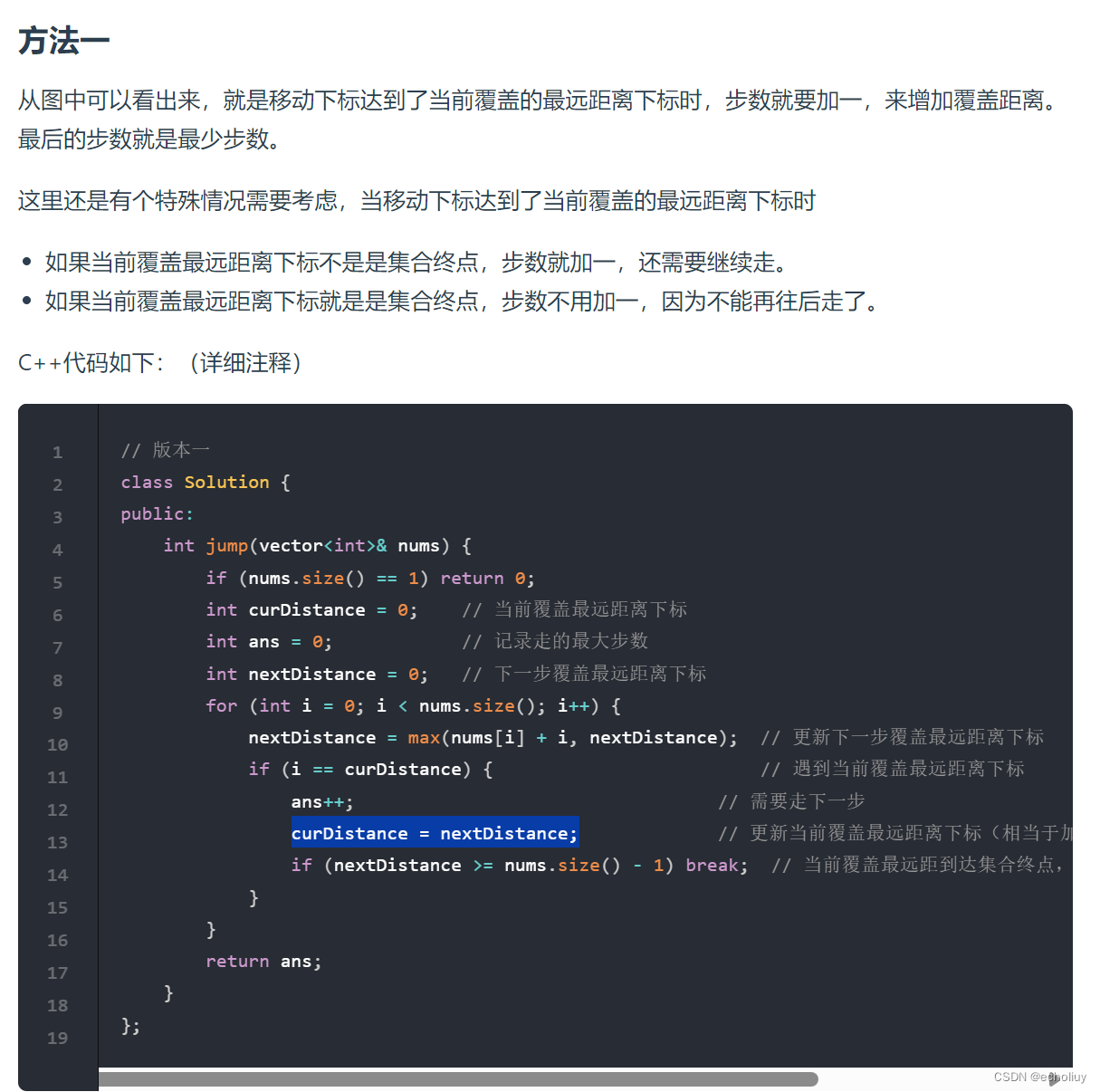
代码:
遇到终点则停止
class Solution {public int jump(int[] nums) {if (nums.size() == 1) return 0;//单一数组int curdis=0; // 当前覆盖最远距离下标int nextdis=0; // 下一步覆盖最远距离下标int ans=0; // 记录走的最大步数for (int i = 0; i < nums.length; i++) {nextdis=Math.max(nextdis,i+nums[i]);// 更新下一步覆盖最远距离下标if(i==curdis){ // 遇到当前覆盖最远距离下标ans++;curdis = nextdis;if(nextdis>=nums.length-1)break;}}return ans;}
}
方法二:处理方法一的特殊情况
// 版本二
class Solution {public int jump(int[] nums) {int result = 0;// 当前覆盖的最远距离下标int curdis = 0;// 下一步覆盖的最远距离下标int nextdis = 0;for (int i = 0; i < nums.length - 1; i++) {nextdis = Math.max(nextdis, i + nums[i]);// 可达位置的改变次数就是跳跃次数if (i == curdis) {curdis = nextdis;result++;}}return result;}
}


项目方舟框架(ArkUI)之NavRouter组件)

)



-docker存储-数据持久化)

)
is required for your GitHub account)







