
一、概念
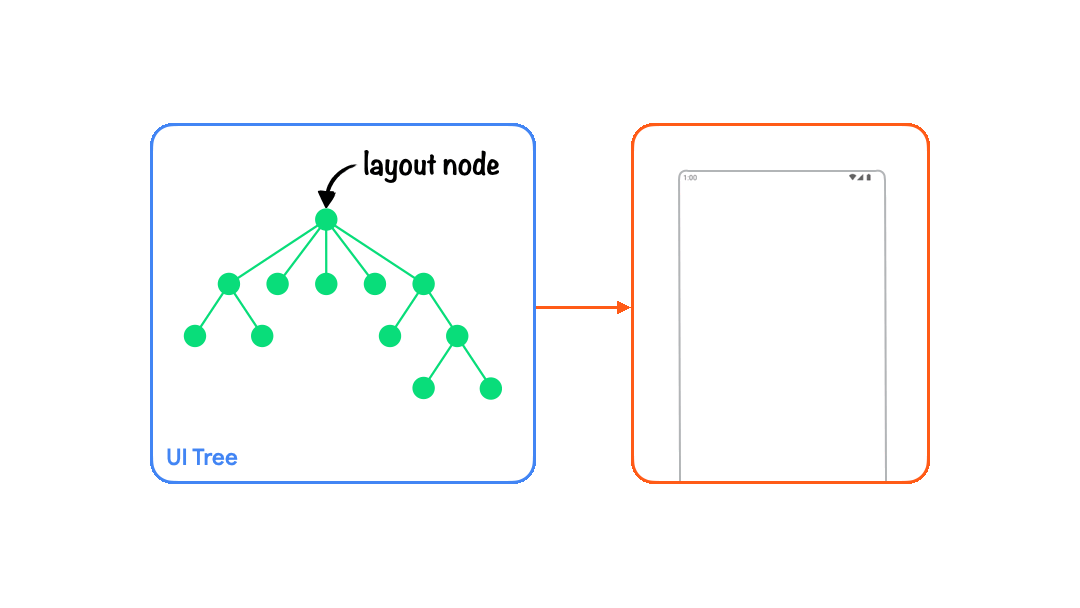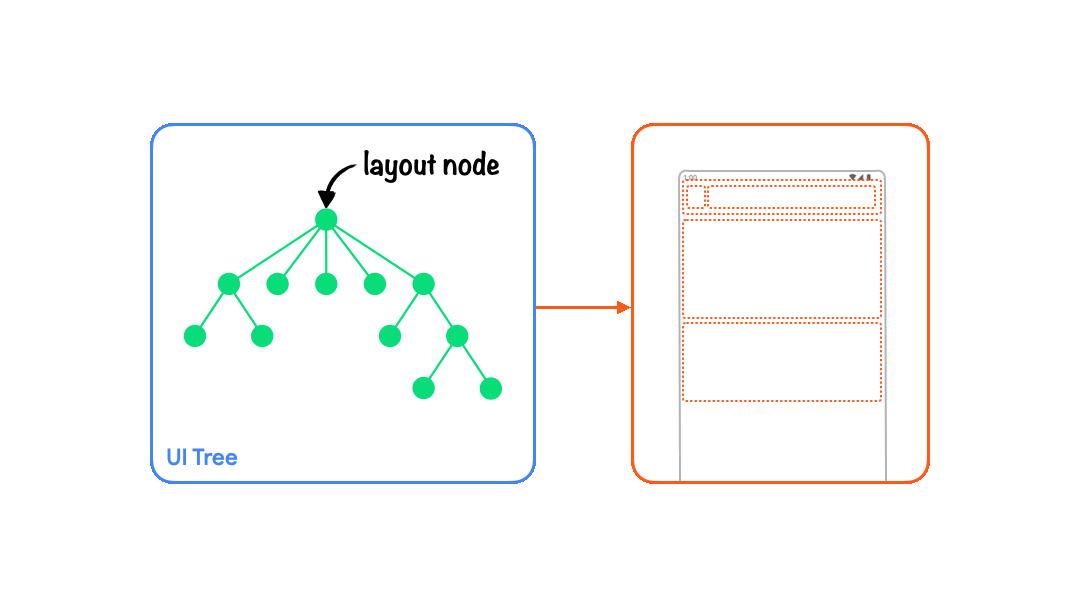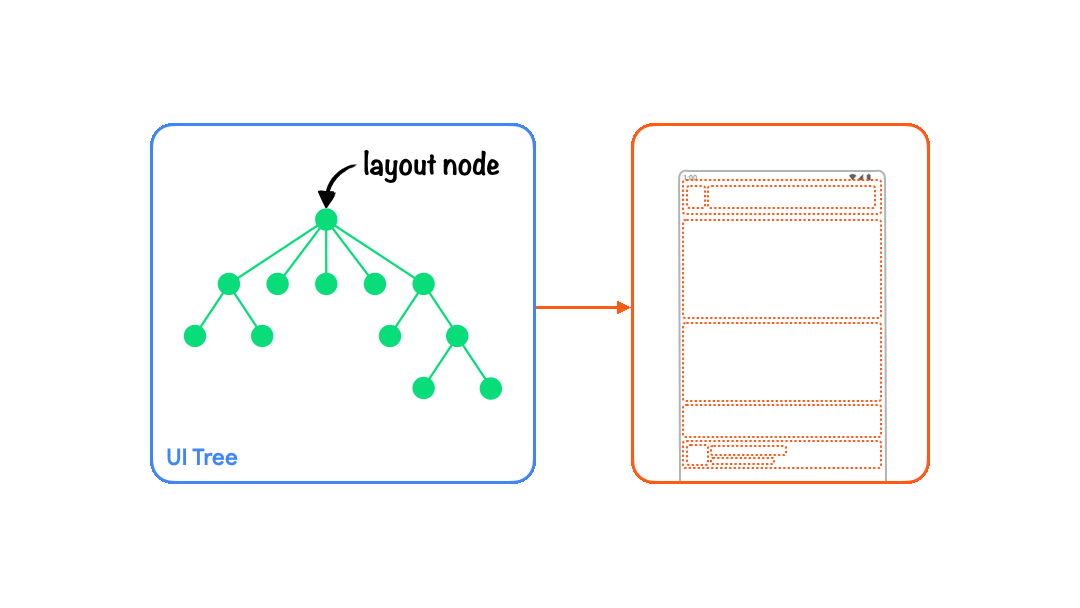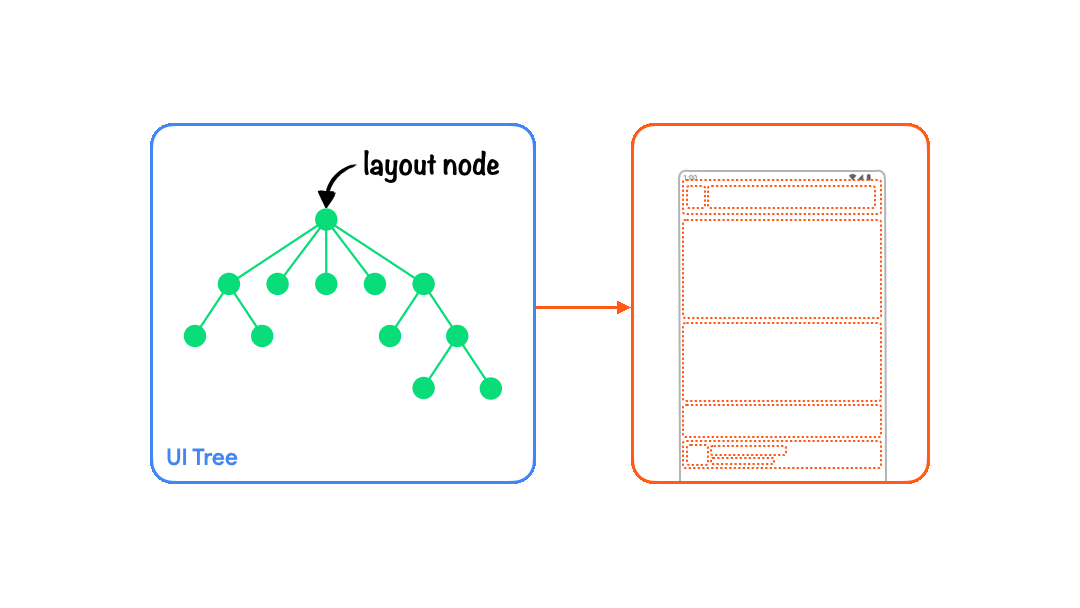
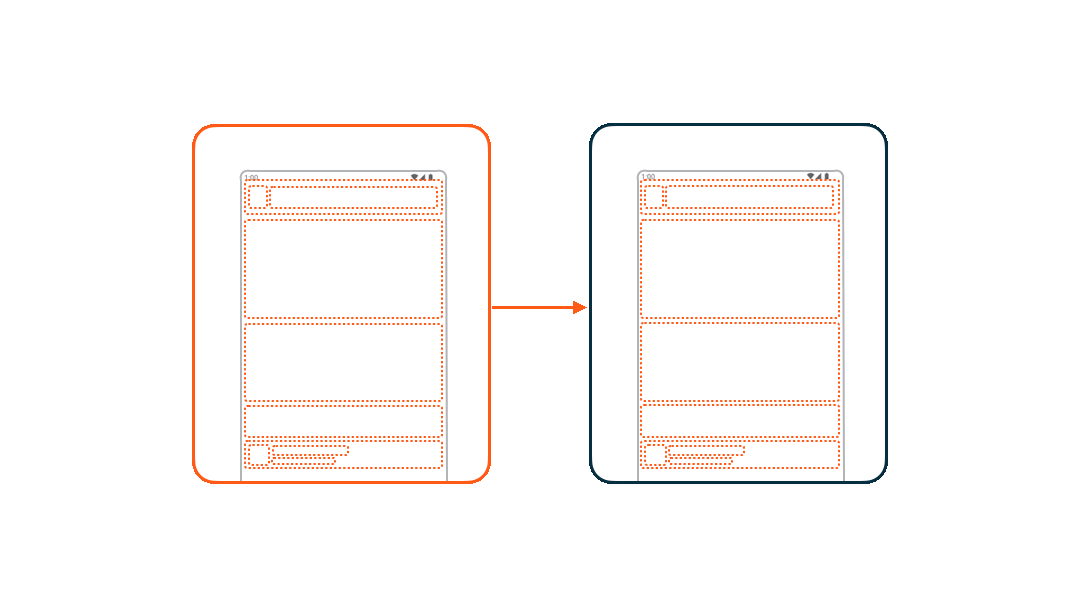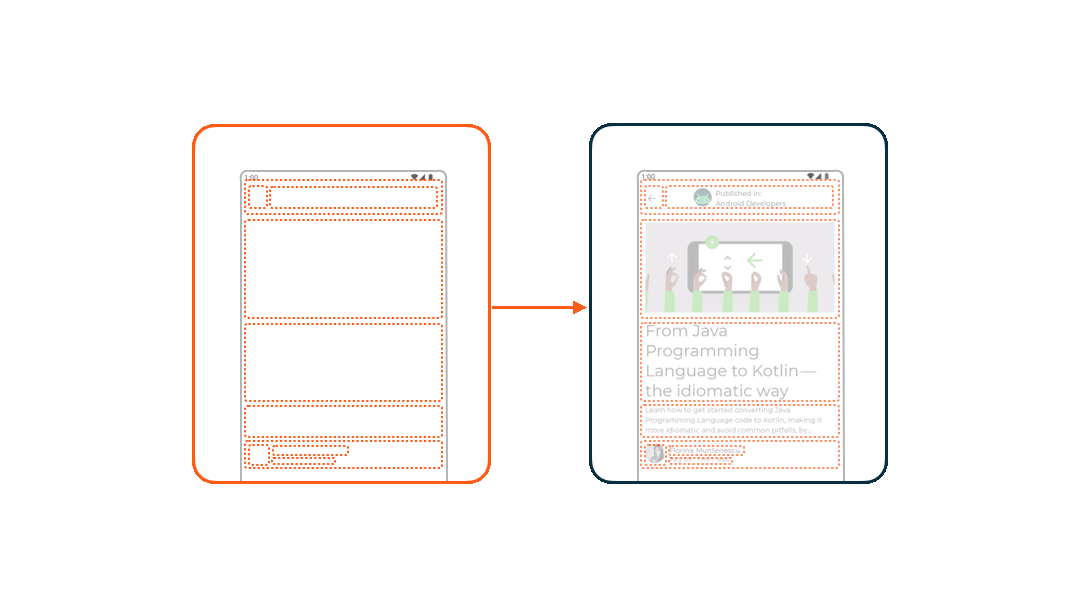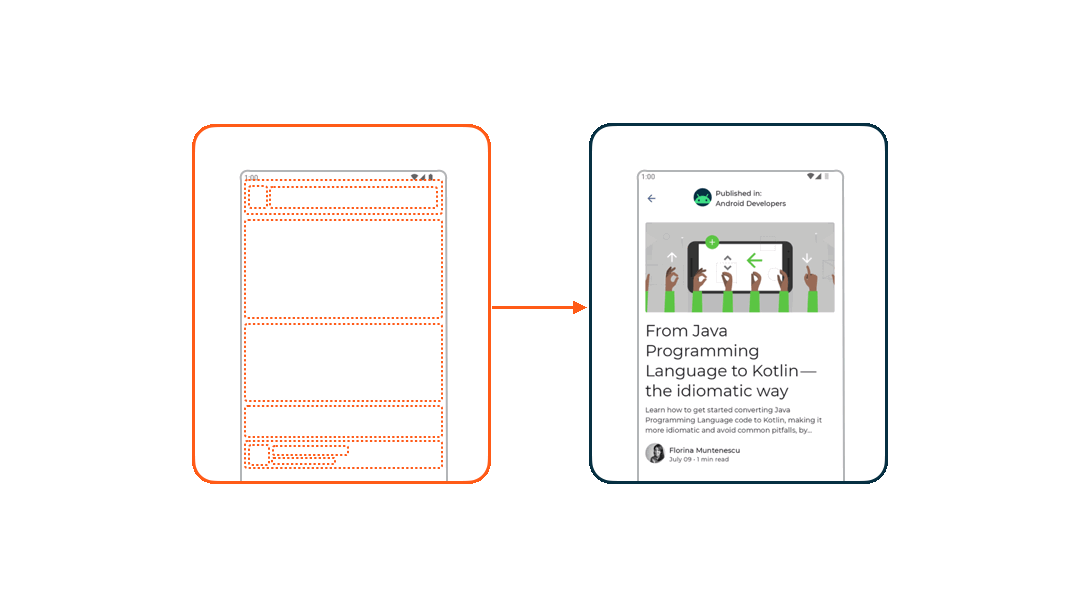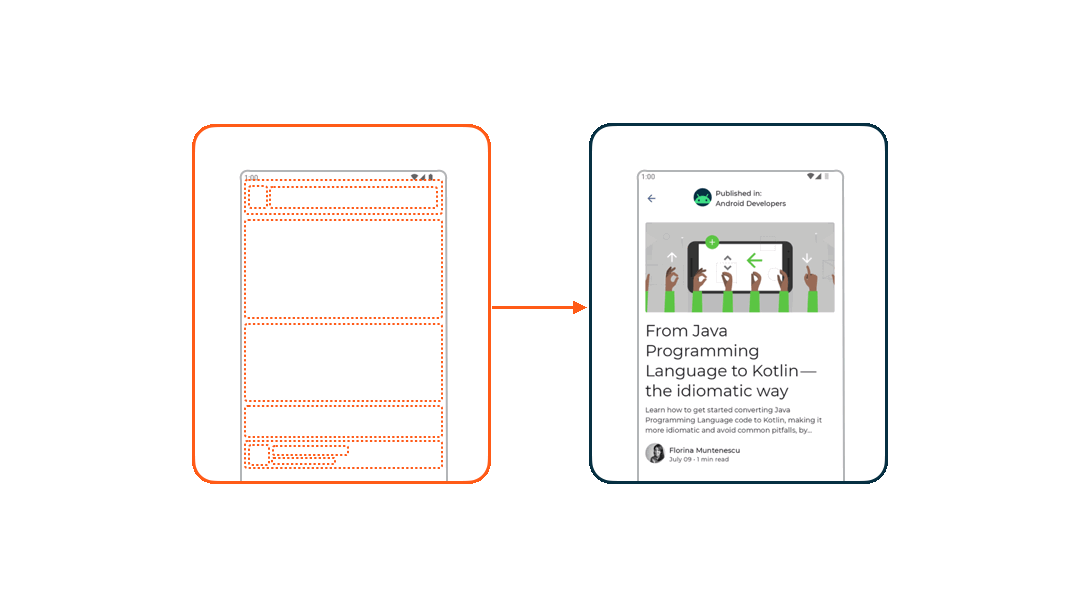
Compose 通过三个阶段把数据转化为UI:组合(要显示什么)、布局(要显示在哪里)、绘制(如何渲染)。
| 组合阶段 Compisition | 界面首次渲染时会将可组合函数转化为一个个布局节点 Layout Node, 使用多叉树的数据结构构建一个UI树。 |
| 布局阶段 Layout | 多叉树中父节点会测量他们的子节点,然后在一个二维空间里进行摆放。通过从上往下测量(如果存在子节点则测量子节点,测量完子节点后决定自身的尺寸)、从下往上摆放(根据子节点的尺寸摆放子节点)来决定该节点的宽高和坐标。 |
| 绘制阶段 Drawing | 所有节点各自绘制自己在屏幕位置的像素。 |

二、举例

2.1 组合阶段 Compisition
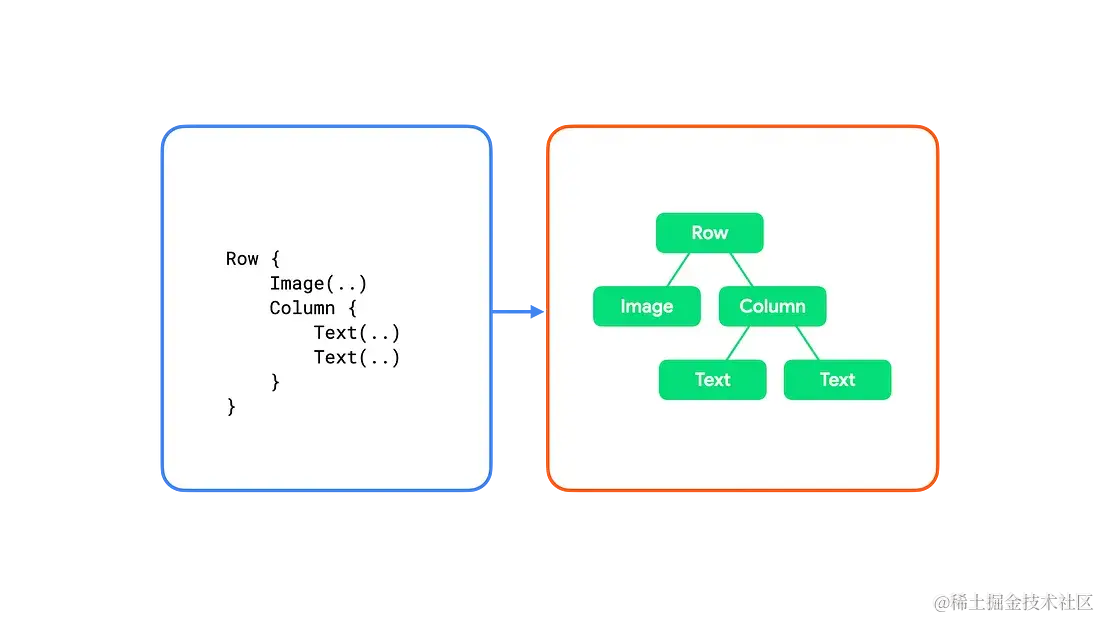
每个 Composable 函数都会映射成UI树的 layout node 。这是一个很简单的例子,事实上 Composable 可以包含逻辑和控制流(if else, when...),在不同的状态下产生不同的UI树。
2.2 布局阶段 Layout
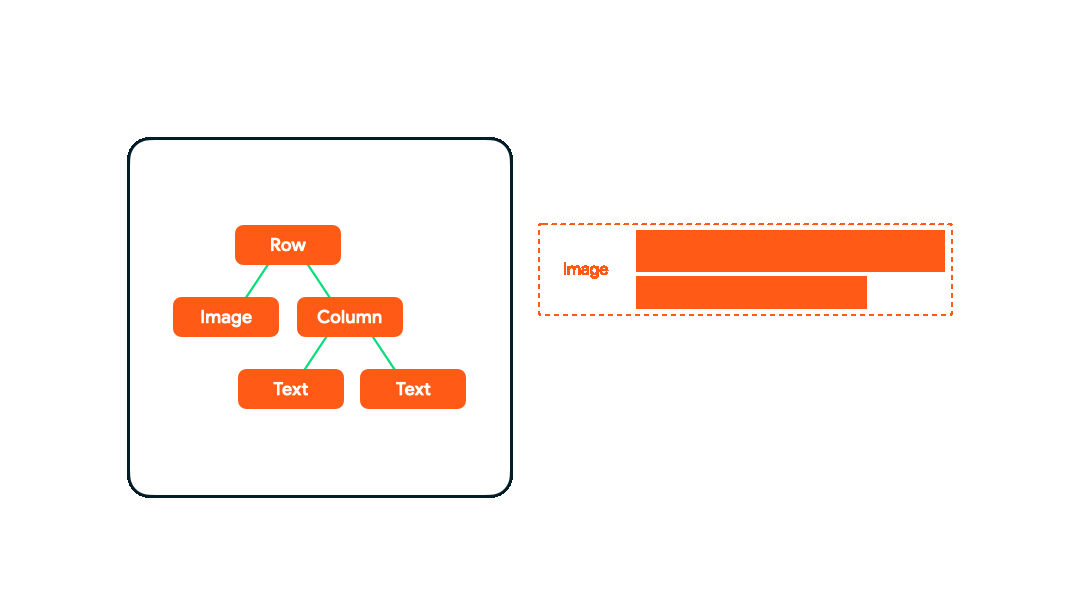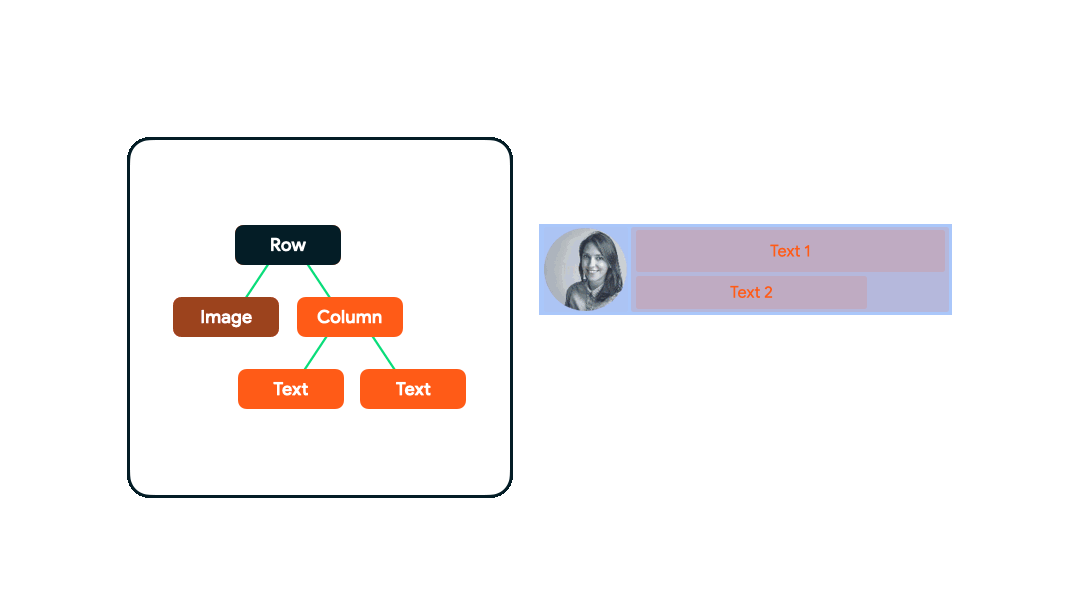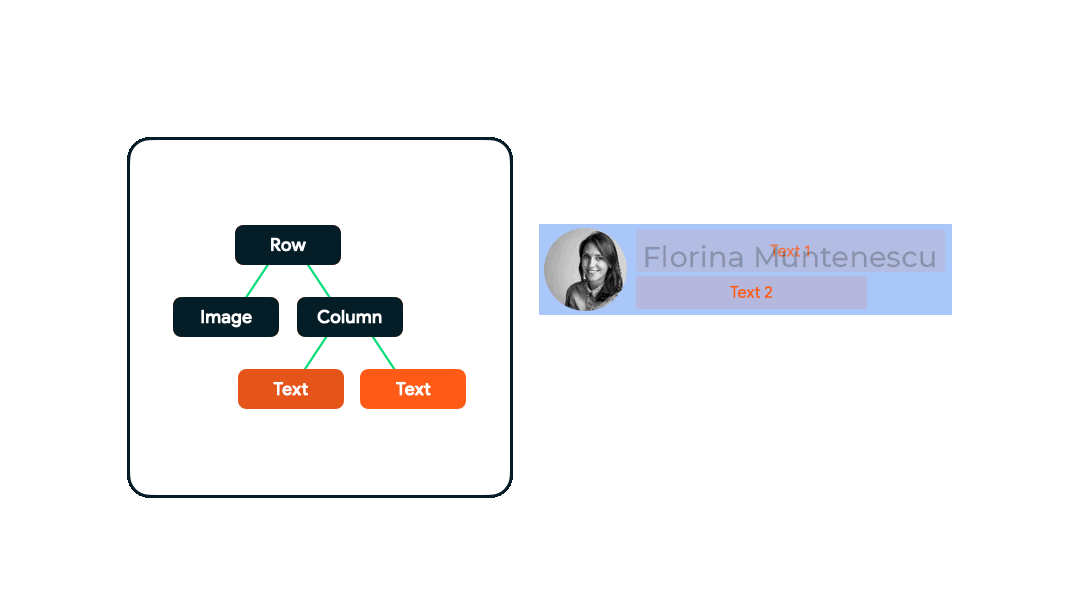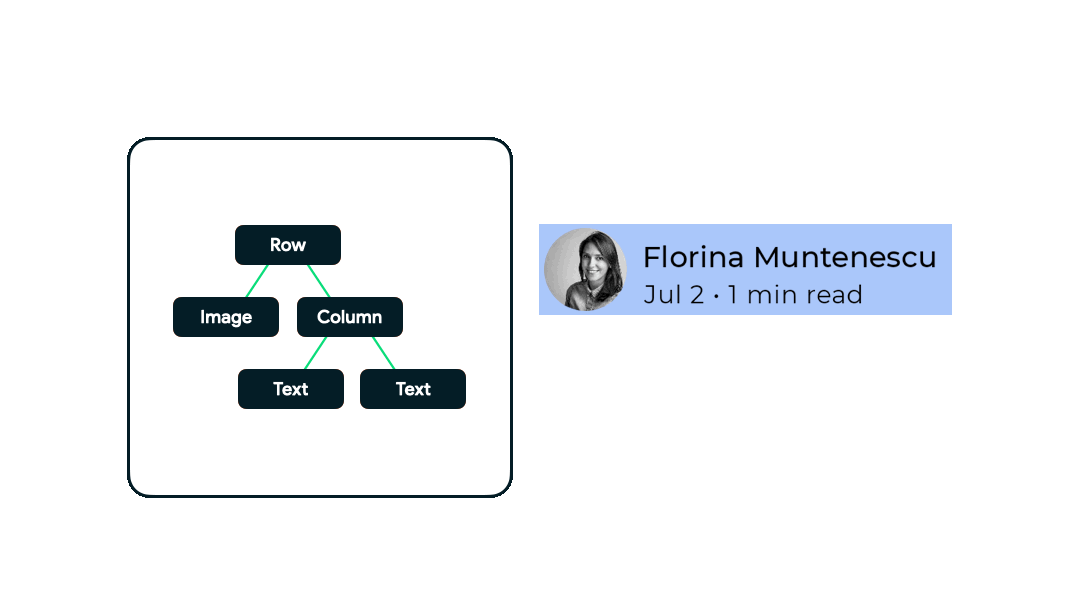
从上往下测量,从下往上摆放:
- 系统要求根节点 Row 测量自身。
- 根节点 Row 要求第一个子元素 Image 测量自身。
- 由于 Image 是叶子节点(没有子节点)能确定自身的尺寸和摆放并上报。
- 根节点 Row 要求第二个子元素 Column 测量自身。由于 Column 是分支节点(有子节点)需要先测量所有子元素来确定自身。
- 父容器 Column 要求第一个子元素 Text 测量自身。
- 由于 Text 是叶子节点能确定自身的尺寸和摆放并上报。
- 父容器 Column 要求第二个子元素 Text 测量自身。
- 由于 Text 是叶子节点能确定自身的尺寸和摆放并上报。
- 父容器 Column 所有子元素都测量摆放完毕,可以确定自身的尺寸和摆放并上报。
- 根节点 Row 所有子元素都测量摆放完毕,可以确定自身的尺寸和摆放。

2.3 绘制阶段 Drawing
同样地,UI树会自顶向下地遍历,每个节点依次在屏幕上绘制自身。首先Row会绘制它自己的内容如背景。然后 Image 绘制自身,再之后到分支节点Column,Column的第一个Text,Column的第二个Text。
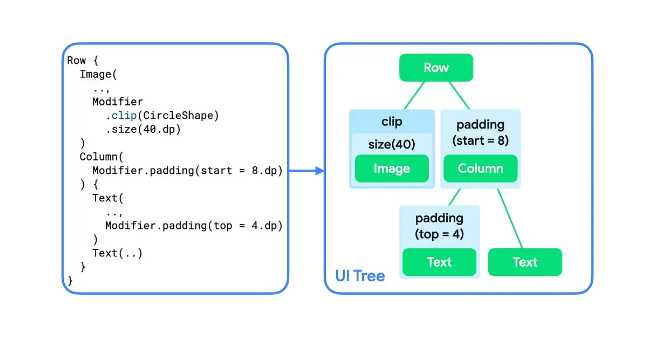
三、Modifier
使用 Modifier 可以更改外观,当链式调用 Modifier 的时候会层层包裹前一个 Modifier 最里层是 Layout Node,详见:Modifier。




)








PyTorch Lightning 实现)

 链表(链式存储))



