这场比赛我觉得题目不是特别难，就是有点难读懂，基本上读懂就差不多会做了。

Problem - A - Codeforces

        1.思路：

                Q1：首先这个题我们一定能确定一个下界答案就是最大值减去最小值，那么我们怎样证明下界答案就是上界答案呢？

                Q2：考虑我们如果得到了下界答案，但是中间产生了a[i - 1] > a[i]的情况，这时候会产生负贡献，因此答案会比我们下界答案更小，因此不会产生比下界答案更大的答案了。

        2.代码：

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 2e5 + 10;
void solve()
{int n;cin >> n;vector<int> a(n);for (int i = 0;i < n;i ++) {cin >> a[i];}sort(a.begin(),a.end());cout << a[n - 1] - a[0] << '\n';
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;cin >> T;while(T --) solve();return 0;
}

Problem - B - Codeforces

        1.思路：

                Q1：首先我们根据样例可以发现每个格子是2条对角线上的，但是我们发现在到达一定的数量后，新格子只会产生一条新对角线的贡献，因此我们考虑如何计算出最少涂多少个能把贡献为2的格子涂完。

                Q2：我们可以多画两个图，则可以发现2*2有2个，3*3有4个，4*4有6个，因此我们可以得出结论2*(n-1)就是我们至少要涂的个数。

                Q3：因此答案就分类讨论一下即可。

        2.代码：

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 2e5 + 10;
void solve()
{int n,k;cin >> n >> k;int rs = (n - 1) * 2;if (k <= rs * 2) {cout << (k + 1) / 2 << '\n';}else {cout << rs + (k - rs * 2) << '\n';}
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;cin >> T;while(T --) solve();return 0;
}

Problem - C - Codeforces

        1.思路：这个题题意有点看不明白，直到看到那个公告才看明白，看明白之后五分钟过了，

思路其实不难，考虑这是一个零和博弈（就是双方的损失加收益之和为零），双方都采取最优策略的话，如果我作为赌场老板，我会采取的策略应该是，在某个临界点让赌徒赢一把，但是赢得钱小于等于输的钱，这样赌徒在做无用功。如果我作为赌徒，我采取得策略应该是，我每一场都要保证就算前面得输了，我这一把也要至少能赢1块这样下注才会有收益，因此做法就出来了，当于每一次我都要下注=之前输的总钱数/倍率+1。如果我们发现最后钱数要大于赌徒初始钱那么赌徒就一定不会成功。

        2.代码：

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 2e5 + 10;
void solve()
{int k,x,a;cin >> k >> x >> a;ll s = 0;for (int i = 1;i <= x + 1;i ++) {ll p = s / (k - 1) + 1;s += p;if (s > a) {cout << "NO" << '\n';return;}}cout << "YES" << '\n';
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;cin >> T;while(T --) solve();return 0;
}

Problem - D - Codeforces

        1.思路：题目大意是给你一棵树，让你选择一个点集，这个点集任意两个点之间不能超过两个危险点（这玩意是拟定得）。

                 考虑如下dp定义dp[i][j]表示i这颗子树有j个危险点得方案数是多少？

                 转移方程如下

                        dp[u][0] = dp[u][1] = 1;(u为危险点or不是危险点得方案数初始为1)

                        1.若u是危险点则子树不能是危险点

                        dp[u][1] -= dp[v][1]

                        2.若u不是危险点则子树有一个危险点

                        dp[u][1] += dp[v][1]

                        3.若u不是危险点，子树一个和零个危险点

                        dp[u][1] *= (dp[v][0] + dp[v][1]);

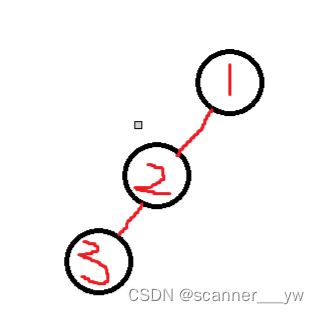
                        为什么要乘上呢？因为这幅图，假如2和3都是危险点，但是对于1子树外得点来说，1子树就1个危险点，因为简单路径不能有重复，如果2通过1得子树走出去了，那么就不能走回来，因此顶多就一个。

                        4.若u不是危险点，则子树有两个危险点。

                        dp[u][2] += dp[v][2];

                        5.若u是危险点，则子树有一个危险点。

                        dp[u][2] += dp[v][1];

                我们可以发现dp[u][0]恒为1，因此可以把dp[u][0]看成1即可。

        2.代码：

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int Mod = 998244353;
void solve()
{int n;cin >> n;vector<vector<int>> g(n);for (int i = 1;i < n;i ++) {int x,y;cin >> x >> y;x --,y --;g[x].push_back(y);g[y].push_back(x);}    auto dfs = [&](auto &&self,int x,int f) -> array<int,2> {array<int,2> dp = {1,0};for (auto &y: g[x]) {if (y != f) {auto ndp = self(self,y,x);dp[0] = (0ll + ndp[0] + 1) * dp[0] % Mod; dp[1] = (0ll + dp[1] + ndp[1] + ndp[0]) % Mod;}}return dp;};auto ans = dfs(dfs,0,-1);cout << (1 + ans[0] + ans[1]) % Mod << '\n';
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;cin >> T;while(T --) solve();return 0;
}

Problem - E - Codeforces

        1.思路：首先看到这种题目我们应该先观察数据范围，发现k<=20，因此出发点从状压开始。  

                Q1：考虑一个事情，就是我们每一对点，我们会在哪里涂呢？

                        我们dfs的时候，从下往上回溯的过程中，我们一定是在最浅的地方涂最优。

                        

                        考虑这幅图，假如有两对分别是1和3，2和3，那么在经过2的时候我们会涂一次边，在1的时候涂一次，但我们只需要涂第一次。

                Q2：怎么判断最优呢？

                        考虑状压DP，f[i]表示满足条件的边集为i的最小需要涂多少次，那么答案就是f[(1 << k) - 1]。状态转移方程为f[i | p(涂的边集)] = min(f[i | p(涂的边集)],f[i] + 1);

        2.代码：

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int inf = 1e9;
void solve()
{int n;cin >> n;vector<vector<int>> g(n);for (int i = 1;i < n;i ++) {int x,y;cin >> x >> y;x --,y --;g[x].push_back(y);g[y].push_back(x);}int k;cin >> k;vector<int> f(1 << k,inf),v(n,0);vector<vector<int>> choice(k);for (int i = 0;i < k;i ++) {int x,y;cin >> x >> y;x --,y --;v[x] ^= 1 << i;v[y] ^= 1 << i;}auto dfs = [&](auto &&self,int x,int f) -> void {for (auto &y: g[x]) {if (y != f) {self(self,y,x);v[x] ^= v[y];}}for (auto &y: g[x]) {if (y != f) {for (int i = 0;i < k;i ++) {if (~v[x] & v[y] & (1 << i)) {choice[i].push_back(v[y]);}}}}};dfs(dfs,0,-1);f[0] = 0;for (int i = 0;i < (1 << k);i ++) {for (int j = 0;j < k;j ++) {for (auto &p: choice[j]) {f[i | p] = min(f[i | p],f[i] + 1);}}}cout << f[(1 << k) - 1] << '\n';
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;cin >> T;while(T --) solve();return 0;
}

Problem - F - Codeforces

        1.思路：我们可以把树形结构转换为序列结构，我们把二叉树的中序遍历看成这颗二叉树的序列，那么我们现在转换为求这个序列是递增序列的方案数。

           考虑两个有限制的相邻节点(i,j)，那么我们把原序列拆成n段来数，最后用乘法原理相乘即可，对于每一段就是每个数有pos[j] - pos[i]个数，并且有j-i+1个位置，我们考虑用隔板法计数即可。

        2.代码：

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
int L[N],R[N],val[N];
int n,k;
vector<int> pos;
const ll Mod = 998244353;
ll inv[N];
void dfs(int x)
{if (x == -1) {return;}dfs(L[x]);pos.pb(val[x]);dfs(R[x]);
}
ll ksm(ll a,ll b)
{ll rs = 1;while (b) {if (b & 1) {rs = rs * a % Mod;}b >>= 1;a = a * a % Mod;}return rs;
}
void init()
{for (int i = N - 1;i >= 1;i --) {inv[i] = ksm(i,Mod - 2);}
}
ll C(int a,int b)
{ll res = 1;for (int i = b,j = a;i >= 1;i --,j --) {res = res * j % Mod * inv[i] % Mod;}return res;
}
void solve()
{cin >> n >> k;for (int i = 1;i <= n;i ++) {cin >> L[i] >> R[i] >> val[i];}pos.clear();pos.pb(1);ll ans = 1;dfs(1);pos.pb(k);for (int i = 0,j = 0;i < sz(pos);i ++) {if (pos[i] == -1) {int l = i,r = i;while (pos[r] == -1) {r ++,i ++;}int d = r - l;ans = (ans * C(pos[r] - pos[l - 1] + d,d)) % Mod;}}cout << ans << '\n';
}
int main()
{init();ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;cin >> T;while(T --) solve();return 0;
}