算法学习——LeetCode力扣回溯篇1

算法学习——LeetCode力扣回溯篇1

在这里插入图片描述

77. 组合

77. 组合 - 力扣（LeetCode）

描述

任何顺序 返回答案。

示例

示例 1：

输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示

  • 1 <= n <= 20
  • 1 <= k <= n

代码解析

回溯遍历法
class Solution {
public:vector<vector<int>> result;vector<int> path;//left是for的开始 ，right是for的结束。当size==k的时候递归结束void tarversal(int left , int right , int k){if(path.size() == k){result.push_back(path);return;}else{for(int i= left ; i <= right ; i++){path.push_back(i);tarversal(i+1 ,right , k);path.pop_back();}return;}}vector<vector<int>> combine(int n, int k) {tarversal(1,n,k);return result;}
};
回溯剪枝法

剪枝是减少无意义循环的过程
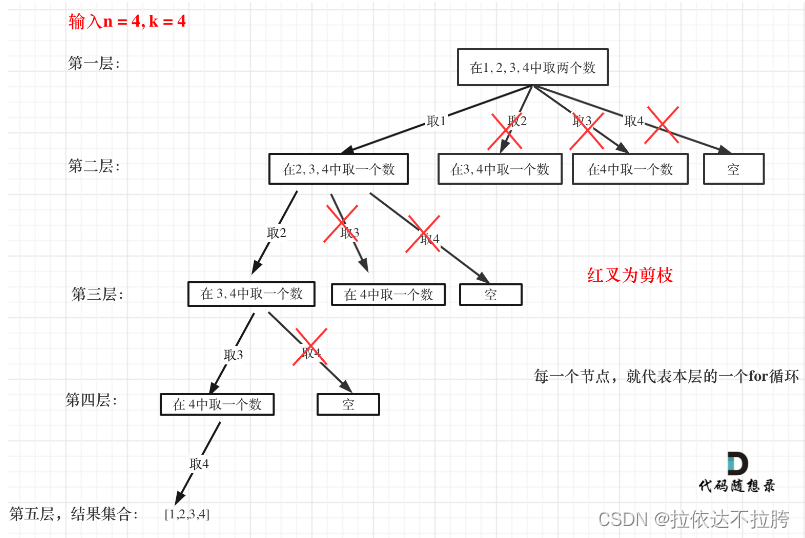
在这里插入图片描述

当输入是n=4，k=4的时候，只有1234符合。我们遍历到2开始时，最多为234，234的长度为3满足长度为4的情况，是无意义的，要剪去。

for(int i= left ; i <= right - (k - path.size()) +1 ; i++) 为剪枝的判断

其中left为遍历的开始，right为遍历的结束。现在还需要找到k - path.size()个点
即 right - left => (k - path.size()) ，为剩下的点可以满足k的要求
=>left <= right - (k - path.size()) +1 ， 其中+1为满足左边闭合。
例，k=3，n=4时，已经选取的为0个（path.size()=0），带入i <= right - ( k - path.size() ) +1 ， i <= 4 - （3-0）+1 ，为i<=2。
即当i最大为从2开始满足，为234 。大于2 剪枝

class Solution {
public:vector<vector<int>> result;vector<int> path;void tarversal(int left , int right , int k){if(path.size() == k){result.push_back(path);return;}else{//i <= right - (k - path.size()) +1为剪枝的过程，避免无意义的循环for(int i= left ; i <= right - (k - path.size()) +1 ; i++){path.push_back(i);tarversal(i+1 ,right , k);path.pop_back();}return;}}vector<vector<int>> combine(int n, int k) {tarversal(1,n,k);return result;}
};

216. 组合总和 III

216. 组合总和 III - 力扣（LeetCode）

描述

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

只使用数字1到9
每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

示例 2:

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。

示例 3:

输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字，我们可以得到的最小和是1+2+3+4 = 10，因为10 > 1，没有有效的组合。

提示

  • 2 <= k <= 9
  • 1 <= n <= 60

代码解析

回溯法无减枝
class Solution {
public:vector<vector<int>> result;vector<int> path;void backtraking(int k, int n , int sum ,int startidx){if(path.size() == k && sum == n){result.push_back(path);return;}else{for(int i= startidx ; i < 10 ; i++){path.push_back(i);backtraking(k,n,sum+i,i+1);path.pop_back();}return;}}vector<vector<int>> combinationSum3(int k, int n) {backtraking(k,n,0,1);return result;}
};
回溯剪枝

剪枝原理同 77题

class Solution {
public:vector<vector<int>> result;vector<int> path;void backtraking(int k, int n , int sum ,int startidx){if(sum > n) return;if(path.size() == k && sum == n){result.push_back(path);return;}else{for(int i= startidx ; i < 10 - (k - path.size()) + 1 ; i++){path.push_back(i);backtraking(k,n,sum+i,i+1);path.pop_back();}return;}}vector<vector<int>> combinationSum3(int k, int n) {backtraking(k,n,0,1);return result;}
};

17. 电话号码的字母组合

17. 电话号码的字母组合 - 力扣（LeetCode）

描述

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例

示例 1：

输入：digits = “23”
输出：[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]

示例 2：

输入：digits = “”
输出：[]

示例 3：

输入：digits = “2”
输出：[“a”,“b”,“c”]

提示

  • 0 <= digits.length <= 4
  • digits[i] 是范围 [‘2’, ‘9’] 的一个数字。

代码解析

字符串
class Solution {
public:const string letterMap[10] = {"", // 0"", // 1"abc", // 2"def", // 3"ghi", // 4"jkl", // 5"mno", // 6"pqrs", // 7"tuv", // 8"wxyz", // 9};vector<string> result;//输入参：转换后的vector ， 从第几个按键开始循环 ， 已经走的路径void backtarcking(vector<int> &digits_i , int startidx , string path){ 	//当路径的长度等于数组的长度，存入结果if(path.size() == digits_i.size() ){result.push_back(path);return;}else{	//第一次循环，循环数字for(int i = startidx ; i < digits_i.size() ; i++){//找到输入数字对应的字母表string tmp = letterMap[digits_i[i]];vector<char> tmp_v(tmp.begin() , tmp.end()) ;//第二次循环，循环每一个数字的字母for(int j=0 ; j < tmp_v.size() ; j++){//递归回溯，开始循环的数字往后走一个，路径加上已经走的路径backtarcking(digits_i, i+1 , path + tmp_v[j]);}}return;}return;}vector<string> letterCombinations(string digits) {//输入为空时直接返回if(digits.size()==0) return result;//字符串转换成vectorvector<int> digits_i;for(auto i:digits) digits_i.push_back( i - '0' );string path;backtarcking(digits_i , 0 , path);return result;}
};
map表
class Solution {
public:vector<string> result;string worldPath;map<char,vector<string>> myMap;void map_init(){myMap.insert(pair<char,vector<string>>('2',{"a","b","c"})) ;myMap.insert(pair<char,vector<string>>('3',{"d","e","f"})) ;myMap.insert(pair<char,vector<string>>('4',{"g","h","i"})) ;myMap.insert(pair<char,vector<string>>('5',{"j","k","l"})) ;myMap.insert(pair<char,vector<string>>('6',{"m","n","o"})) ;myMap.insert(pair<char,vector<string>>('7',{"p","q","r","s"})) ;myMap.insert(pair<char,vector<string>>('8',{"t","u","v"})) ;myMap.insert(pair<char,vector<string>>('9',{"w","x","y","z"})) ;// for(auto it:myMap)//      cout<<it.first<<':'<<(it.second)[0]<<endl;// cout<<myMap['2'].size();}void dfs(string digits , int fir ){if( worldPath.size() == digits.size()){result.push_back(worldPath);return;}char num = digits[fir];for(int j=0 ; j< myMap[num].size() ;j++){worldPath += myMap[num][j];dfs(digits,fir+1);worldPath.pop_back();}return;}vector<string> letterCombinations(string digits) {if(digits.size()==0) return result;map_init();dfs(digits,0);return result;}
};

39. 组合总和

39. 组合总和 - 力扣（LeetCode）

描述

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例

示例 1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

提示

  • 1 <= candidates.length <= 30
  • 2 <= candidates[i] <= 40
  • candidates 的所有元素 互不相同
  • 1 <= target <= 40

代码解析

暴力回溯（无剪枝，时间复杂度高）
class Solution {
public:vector<vector<int>> result;vector<int> path;int sum;void backtracking(vector<int>& candidates, int target , int sum){	//检测目标大于时返回if(sum > target) return;if(sum == target){//排序后发现是新结果插入vector<int> tmp(path.begin(),path.end());sort(tmp.begin(),tmp.end());auto it = find(result.begin(),result.end(),tmp);if(it == result.end()) result.push_back(tmp);return;}//无任何限制回溯for(int i = 0 ; i < candidates.size() ;i++){path.push_back(candidates[i]);backtracking(candidates,target,sum+candidates[i]);path.pop_back();}return;}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {backtracking(candidates,target,0);return result;}
};
回溯剪枝
class Solution {
public:vector<vector<int>> result;vector<int> path;int sum;void backtracking(vector<int>& candidates, int target , int sum , int indnx){if(sum > target) return;if(sum == target){result.push_back(path);return;}//剪枝，因为之前已经对输入进行排序，当发现加上i点的值大于目标后，后面的也都大于for(int i = indnx ; i < candidates.size() && sum+candidates[i] <= target ;i++){path.push_back(candidates[i]);//递归的下一个指针和当前一样都是i，不是i+1 //因为一个数可以重复的使用，不能重复是i+1backtracking(candidates,target,sum+candidates[i] , i);path.pop_back();}return;}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {//对输入进行排序，方便后面循环sort(candidates.begin(),candidates.end());backtracking(candidates,target,0,0);return result;}
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/682942.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

【机器学习案例4】为机器学习算法编码分类数据【含源码】

【机器学习案例4】为机器学习算法编码分类数据【含源码】

目录 编码分类数据 序数编码 标签编码 一次性编码 目标编码 目标编码的优点 目标编码的缺点 在现实生活中，收集的原始数据很少采用我们可以直接用于机器学习模型的格式，即数值型数据。因此，需要进行一些预处理，以便以正确的格式呈现数据、选择信息丰富的数据或降低其…
阅读更多...
【C++函数探幽】内联函数inline

【C++函数探幽】内联函数inline

&#x1f4d9; 作者简介 &#xff1a;RO-BERRY &#x1f4d7; 学习方向&#xff1a;致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 &#x1f4d2; 日后方向 : 偏向于CPP开发以及大数据方向&#xff0c;欢迎各位关注&#xff0c;谢谢各位的支持 目录 1. 前言2.概念3.特性…
阅读更多...
GPT-4带来的思想火花

GPT-4带来的思想火花

GPT-4能够以其强大的生成能力和广泛的知识储备激发出众多思想火花。它能够在不同的情境下生成新颖的观点、独特的见解和富有创意的解决方案&#xff0c;这不仅有助于用户突破思维定势&#xff0c;还能促进知识与信息在不同领域的交叉融合。 对于研究者而言&#xff0c;GPT-4可能…
阅读更多...
浅谈业务场景中缓存的使用

浅谈业务场景中缓存的使用

业务场景中缓存的使用 一、背景二、缓存分类1.本地缓存2.分布式缓存 三、缓存读写模式1.读请求2.写请求 四、缓存穿透1.缓存空对象2.请求校验3.请求来源限制4.布隆过滤器 五、缓存击穿1.改变过期时间2.串行访问数据库 六、缓存雪崩1.避免集中过期2.提前更新缓存 七、缓存与数据…
阅读更多...
【MATLAB】鲸鱼算法优化混合核极限学习机(WOA-HKELM)回归预测算法

【MATLAB】鲸鱼算法优化混合核极限学习机(WOA-HKELM)回归预测算法

有意向获取代码&#xff0c;请转文末观看代码获取方式~也可转原文链接获取~ 1 基本定义 鲸鱼算法优化混合核极限学习机&#xff08;WOA-HKELM&#xff09;回归预测算法是一种结合鲸鱼优化算法和混合核极限学习机的混合算法。其原理主要包含以下几个步骤&#xff1a; 初始化&am…
阅读更多...
UniApp学习之旅：从入门到快速上手

UniApp学习之旅：从入门到快速上手

随着移动互联网的迅猛发展&#xff0c;跨平台应用开发成为了开发者们的热门选择。UniApp&#xff0c;作为一款使用Vue.js开发所有前端应用的框架&#xff0c;因其简单、高效、易上手的特性&#xff0c;受到了广大开发者的青睐。本文将带你走进UniApp的世界&#xff0c;从基础学…
阅读更多...
【leetcode】深搜、暴搜、回溯、剪枝（C++）2

【leetcode】深搜、暴搜、回溯、剪枝（C++）2

深搜、暴搜、回溯、剪枝&#xff08;C&#xff09;2 一、括号生成1、题目描述2、代码3、解析 二、组合1、题目描述2、代码3、解析 三、目标和1、题目描述2、代码3、解析 四、组合总和1、题目描述2、代码3、解析 五、字母大小写全排列1、题目描述2、代码3、解析 六、优美的排列1…
阅读更多...
鸿蒙视频播放器，主要包括视频获取和视频播放功能：

鸿蒙视频播放器，主要包括视频获取和视频播放功能：

鸿蒙视频播放器&#xff0c;主要包括视频获取和视频播放功能&#xff1a; 1 获取本地视频或者网络视频。 2 通过media.createAVPlayer创建播放器AVPlayer&#xff0c;然后进行视频播放。 3 通过VideoController进行AVPlayerState的状态管理&#xff0c;如开始&#xff0c;停止&…
阅读更多...
2.15 字符串练习

2.15 字符串练习

1、选择题 1.1、有以下程序 int main() { char a[7]"a0\0a0\0";int i,j; isizeof(a); jstrlen(a); printf("%d %d\n",i,j); } //strlen求出字符串的长度&#xff0c;其实是字符串中字符的个数&#xff0c;不包括\0 程序运行后的输出结果是 C…
阅读更多...
K210开发环境搭建（VS Code）

K210开发环境搭建（VS Code）

一、新建一个文件夹&#xff0c;就叫K210 二、再K210文件夹里面再新建一个文件夹&#xff0c;就叫CMake 三、找到官方提供的资料包里的cmake安装包&#xff0c; 或者直接去cmake官方下载网址进行下载 CMake官方下载网址&#xff1a;https://cmake.org/download/ 四、双击安装…
阅读更多...
Screw自动生成数据库文档

Screw自动生成数据库文档

Screw简介 官方地址 Screw可以根据数据库中的表自动生成HTML、Word、Markdown格式的文档。 Springboot 3.1集成 生成Springboot项目 Spring Initializr Maven依赖 <dependency><groupId>cn.smallbun.screw</groupId><artifactId>screw-core</…
阅读更多...
Nginx实战：日志按天分割

Nginx实战：日志按天分割

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 目录 前言 一、方式1&#xff1a;定时任务执行分割脚本 1.分割日志脚本 2.添加定时任务 二、方式2&#xff1a;logrotate配置分割 1.logrotate简单介绍 2.新增切割ngi…
阅读更多...
FT2232调试记录（3）

FT2232调试记录（3）

FT2232调试记录&#xff08;1&#xff09;: FT2232调试记录&#xff08;2&#xff09;: FT2232调试记录&#xff08;3&#xff09;: FT2232 SPI读写函数: 参照SPI提供的文档&#xff1a; 工程&#xff1a; SPI 写函数&#xff1a; FT_STATUS write_byte(FT_HANDLE handle…
阅读更多...
再利用系统盘时，如何删除恢复分区(Recovery Partition)

再利用系统盘时，如何删除恢复分区(Recovery Partition)

系统盘有一个Recovery Partition&#xff0c;记录了重要的系统信息&#xff0c;不能删除。 Windows 10的 Disk Managment 不提供用户删除这个Partition的选项。 近日我插入一块原系统盘&#xff0c;Format后作为DataDisk&#xff0c;此时需要删除这块硬盘上的RecoveryPartition…
阅读更多...
机器学习系列——（二十一）神经网络

机器学习系列——（二十一）神经网络

引言 在当今数字化时代&#xff0c;机器学习技术正日益成为各行各业的核心。而在机器学习领域中&#xff0c;神经网络是一种备受瞩目的模型&#xff0c;因其出色的性能和广泛的应用而备受关注。本文将深入介绍神经网络&#xff0c;探讨其原理、结构以及应用。 一、简介 神经网…
阅读更多...
【碎片知识点】安装Linux系统 VMware与kali

【碎片知识点】安装Linux系统 VMware与kali

天命&#xff1a;VMware就是可以运行操作系统的载体&#xff0c;kali就是Linux的其中一个分支 天命&#xff1a;Linux有两个分支版本&#xff1a;centos与ubuntu&#xff0c;kali底层就是ubuntu&#xff08;所有Linux用起来都差不多&#xff0c;没啥区别&#xff09; 天命&…
阅读更多...
CSS之选择器、优先级、继承

CSS之选择器、优先级、继承

1.CSS选择器 常用的选择器 <body><div class"parent"><div id"one" style"background: blue" class"child">1<div class"one_one">11</div><div style"background-color: blueviole…
阅读更多...
2024LeetCode分类刷题

2024LeetCode分类刷题

一、数组 88. 合并两个有序数组 public void merge(int[] nums1, int m, int[] nums2, int n) {int p1 0, p2 0;int[] sorted new int[m n];while (p1 < m || p2 < n) {int current;if (p1 m) {current nums2[p2];} else if (p2 n) {current nums1[p1];} else i…
阅读更多...
每日一题——数字翻转

每日一题——数字翻转

题目; 这道题看似是很简单的回文数 实则就是很简单的回文数 但是需要注意的一点是负数 可以在开头就进行判断&#xff0c;如果N<0的话就令N-N&#xff0c;将所有数都转成正数就好办了 上代码&#xff1a; #include <iostream> #include<string> #include<…
阅读更多...
4核16G服务器价格腾讯云PK阿里云

4核16G服务器价格腾讯云PK阿里云

4核16G服务器租用优惠价格26元1个月&#xff0c;腾讯云轻量4核16G12M服务器32元1个月、96元3个月、156元6个月、312元一年&#xff0c;阿腾云atengyun.com分享4核16服务器租用费用价格表&#xff0c;阿里云和腾讯云详细配置报价和性能参数表&#xff1a; 腾讯云4核16G服务器价…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023