欢迎关注我的CSDN:https://spike.blog.csdn.net/
本文地址:https://spike.blog.csdn.net/article/details/136055085
VQGAN: Taming Transformers for High-Resolution Image Synthesis, CVPR 2021
VQGAN: 改良 Transformer 模型以实现高清图像合成

源码:https://github.com/CompVis/taming-transformers
为了学习顺序数据的长距离交互,Transformers在各种任务上持续展现出最先进的结果。与卷积神经网络(CNNs)相比,Transformer不包含优先考虑局部交互的归纳偏置(Inductive Bias)。这使得Transformer具有表达能力,但也使得Transformer在处理长序列,例如高分辨率图像时,计算上不可行。本文展示如何将CNNs的归纳偏置的有效性,与Transformer的表达能力相结合,使得VQGAN能够建模,并且合成高分辨率图像。本文展示如何(i)使用CNNs学习一个富含上下文的图像成分词汇表,然后(ii)利用Transformers高效地建模,在高分辨率图像中的组合。本文的方法可以很容易地应用于条件合成任务(Conditional Synthesis Tasks),其中,非空间信息,例如对象类别,和空间信息,例如分割,都可以控制生成的图像。特别地,本文展示了使用Transformers在语义引导下,合成百万像素(1024x1024)图像的第一个结果,并且,在类条件ImageNet上获得了自回归模型中的最先进水平。
本文获得一个有效和富有表现力的模型的关键启发是,卷积和Transformer架构结合起来,可以建模视觉世界的组合性质:本文使用卷积方法来高效地学习一个包含丰富上下文的视觉部件的码本,然后学习一个全局组合的模型。这些组合中的长距离交互,需要一个富有表现力的Transformer架构,来建模其构成视觉部件的分布。此外,本文利用对抗方法,来确保局部部件的字典,捕捉到感知上重要的局部结构,从而减轻了用Transformer架构建模低级统计的需要。让Transformer专注于独特优势——建模长距离关系——使它们能够生成高分辨率的图像,这是以前无法达到的。本文的方法通过条件信息来控制生成的图像,条件信息包括期望的对象类别或空间布局。最后,实验表明,本文的方法保留了Transformer的优势,超越了基于卷积架构的先进的基于码本的方法。
Transformer的机制, d k d_{k} dk 与 d v d_v dv 的维度相同,Mask元素成,即:

本文使用一个卷积VQGAN来学习一个包含丰富上下文的视觉部分的编码本(Codebook),其组合随后由一个自回归的Transformer架构进行建模。一个离散的编码本提供了这些架构之间的接口,而一个基于块(patch-based)的判别器,使得在保持高感知质量的同时,实现强压缩。这种方法将卷积方法的效率引入了基于变换器的高分辨率图像合成。如图:
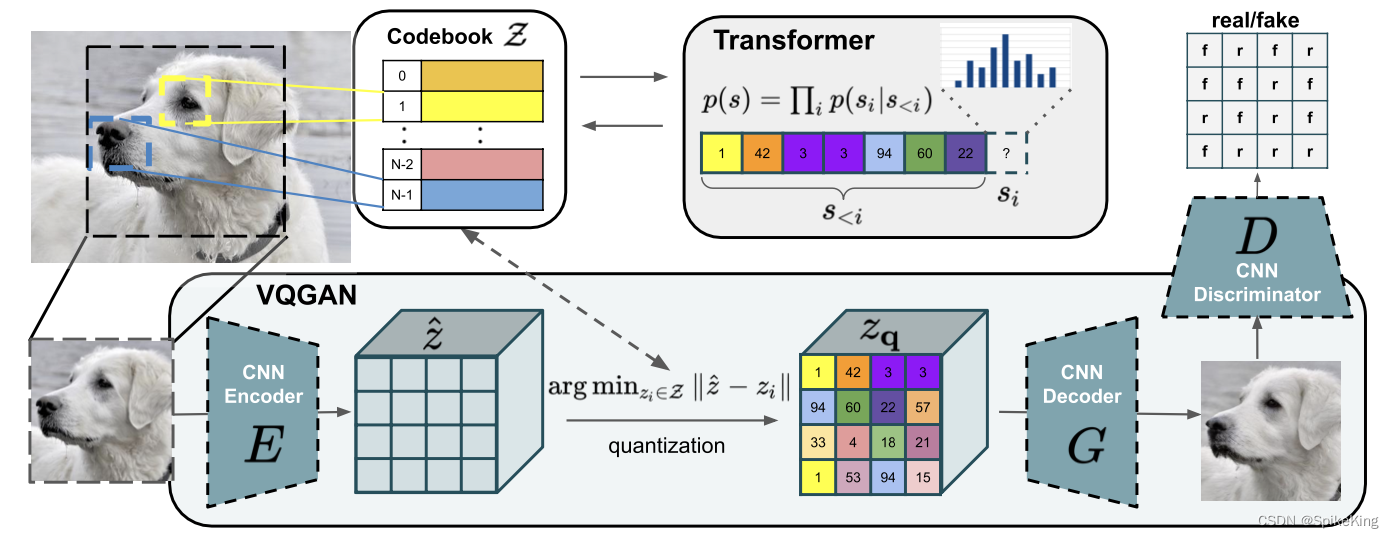
VQGAN的Encoder和Decoder结构:

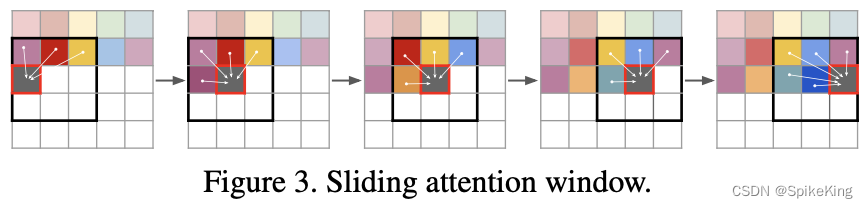
滑动注意力窗口(Sliding attention window):
在本文设置中,Transformer统一广泛的图像合成任务。本文展示了在不同的条件输入和数据集上的256×256合成结果,所有这些结果都是用相同的方法获得的,即利用有效的基于CNN的VQGAN架构的归纳偏置,结合Transformer架构的表达能力。
- 第1行:从无条件训练的ImageNet上的补全。
- 第2行:在RIN上的深度到图像。
- 第3行:在ADE20K上的语义引导合成。
- 第4行:在DeepFashion上的姿态引导人物生成。
- 第5行:在RIN上的类条件样本。
即:

将滑动注意力窗口(Sliding Attention Window)方法,应用于各种条件图像合成任务。
- 第1行:在RIN上的深度到图像。
- 第2行:在IN上的随机超分辨率。
- 第3和第3行:在 S-FLCKR 上的语义合成
- 第5行:在 IN上的边缘引导合成。
生成的图像大小在368×496和1024×576之间变化,因此最好放大查看。

其他:
Frechet Inception Distance (FID) Score,即FID score是一种评估生成模型图片质量的指标,使用了Inception Net-V3分类器,来评估生成图片的清晰度和多样性。基本思想是,用分类器提取真实图片和生成图片的特征向量,然后计算两组特征向量的Fréchet距离,这个距离越小,说明生成图片越接近真实图片。具体的计算公式如下:
FID ( X , G ) = ∥ μ X − μ G ∥ 2 2 + Tr ( Σ X + Σ G − 2 ( Σ X Σ G ) 1 / 2 ) \text{FID}(X, G) = \|\mu_X - \mu_G\|_2^2 + \text{Tr}(\Sigma_X + \Sigma_G - 2(\Sigma_X\Sigma_G)^{1/2}) FID(X,G)=∥μX−μG∥22+Tr(ΣX+ΣG−2(ΣXΣG)1/2)
其中, X X X是真实图片的集合, G G G是生成图片的集合, μ X \mu_X μX和 μ G \mu_G μG是两组特征向量的均值, Σ X \Sigma_X ΣX和 Σ G \Sigma_G ΣG是两组特征向量的协方差矩阵, Tr \text{Tr} Tr是矩阵的迹, ∥ ⋅ ∥ 2 \|\cdot\|_2 ∥⋅∥2是二范数。
FID score与之前的IS(Inception Score)相比,有以下几个优点:
- FID score同时考虑了生成图片的清晰度和多样性,而IS只考虑了多样性。
- FID score与人类的主观评价更一致,而IS有时会出现与人类判断不一致的情况。
- FID score可以用于不同的条件生成任务,而IS只适用于无条件生成任务。
FID score也有一些局限性,例如:
- FID score依赖于分类器的选择,不同的分类器可能会导致不同的结果。
- FID score需要有一个足够大的真实图片集合作为参考,这在一些特定领域可能不容易获得。
- FID score不能反映生成图片的语义一致性,例如是否符合给定的条件或约束。
LDM: Latent Diffusion Model, Patrick Esser, Runway ML (Stable Diffusion 的公司)

Runway 公司:




 | 基于imgui-SFML改进自由落体小球)

)




![[leetcode]买卖股票的最佳时机 (动态规划)](http://pic.xiahunao.cn/[leetcode]买卖股票的最佳时机 (动态规划))







 + egl + opengles 纹理贴图进阶实例(四))