11.114. 二叉树展开为链表

给你二叉树的根结点 root ，请你将它展开为一个单链表：

• 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
• 展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [0]
输出：[0]

提示：

• 树中结点数在范围 [0, 2000] 内
• -100 <= Node.val <= 100

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

思路：

可以发现展开的顺序其实就是二叉树的先序遍历。算法和 94 题中序遍历的 Morris 算法有些神似，我们需要两步完成这道题。
1.将左子树插入到右子树的地方
2.将原来的右子树接到左子树的最右边节点
考虑新的右子树的根节点，一直重复上边的过程，直到新的右子树为 null
可以看图理解下这个过程。

    1/ \2   5/ \   \
3   4   6//将 1 的左子树插入到右子树的地方1\2         5/ \         \3   4         6        
//将原来的右子树接到左子树的最右边节点1\2          / \          3   4  \5\6//将 2 的左子树插入到右子树的地方1\2          \          3       4  \5\6   //将原来的右子树接到左子树的最右边节点1\2          \          3      \4  \5\6         ......

代码：java

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public void flatten(TreeNode root) {while (root != null) { //左子树为 null，直接考虑下一个节点if (root.left == null) {root = root.right;} else {// 找左子树最右边的节点TreeNode pre = root.left;while (pre.right != null) {pre = pre.right;} //将原来的右子树接到左子树的最右边节点pre.right = root.right;// 将左子树插入到右子树的地方root.right = root.left;root.left = null;// 考虑下一个节点root = root.right;}}
}}

12.105. 从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

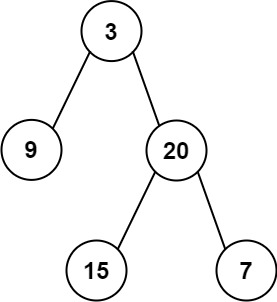
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder 和 inorder 均 无重复 元素
• inorder 均出现在 preorder
• preorder 保证 为二叉树的前序遍历序列
• inorder 保证 为二叉树的中序遍历序列

思路：

前序遍历是：根左右；中序是：左根右。

因此顺序肯定是，先根据前序序列确定根节点，然后按照根节点对中序序列做划分，序列以左为左孩子，序列以右是右孩子。这是手写题思路！

代码思路：

算法流程：
递推参数： 根节点在前序遍历的索引 root 、子树在中序遍历的左边界 left 、子树在中序遍历的右边界 right 。

终止条件： 当 left > right ，代表已经越过叶节点，此时返回 null。

递推工作：

        建立根节点 node ： 节点值为 preorder[root] 。
        划分左右子树： 查找根节点在中序遍历 inorder 中的索引 i 。
        构建左右子树： 开启左右子树递归。

代码：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:def recur(root, left, right):if left > right: return                               # 递归终止node = TreeNode(preorder[root])                       # 建立根节点i = dic[preorder[root]]                               # 划分根节点、左子树、右子树node.left = recur(root + 1, left, i - 1)              # 开启左子树递归node.right = recur(i - left + root + 1, i + 1, right) # 开启右子树递归return node                                           # 回溯返回根节点#     i - left + root + 1含义为 `根节点索引 + 左子树长度 + 1`dic, preorder = {}, preorderfor i in range(len(inorder)):dic[inorder[i]] = ireturn recur(0, 0, len(inorder) - 1)

13.437. 路径总和 III

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

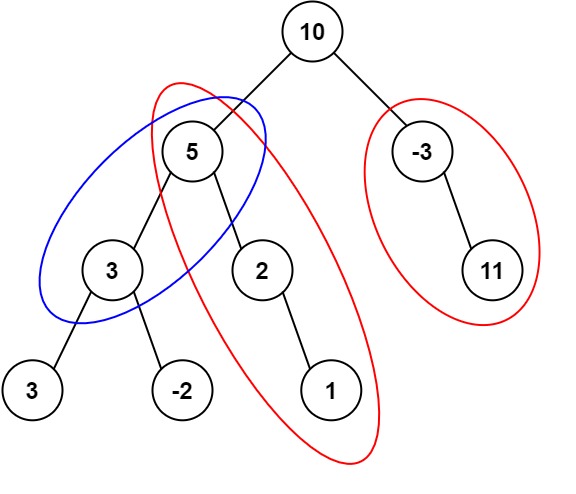
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

提示:

• 二叉树的节点个数的范围是 [0,1000]
• -10^9 <= Node.val <= 10^9 
• -1000 <= targetSum <= 1000

思路：

最开始，想着深度优先搜索，然后给每一个叶节点对应一个列表，然后对列表里的元素，求前缀和。

代码：

class Solution {
public:int rootSum(TreeNode* root, long targetSum) {if (!root) {return 0;}int ret = 0;if (root->val == targetSum) {ret++;} ret += rootSum(root->left, targetSum - root->val);ret += rootSum(root->right, targetSum - root->val);return ret;}int pathSum(TreeNode* root, int targetSum) {if (!root) {return 0;}int ret = rootSum(root, targetSum);ret += pathSum(root->left, targetSum);ret += pathSum(root->right, targetSum);return ret;}
};