双指针
用于解决一类基于子段的统计问题
子段就是:数组中连续的一段
可以用一个
闭区间来表示数组中的连续一段
这个方法核心就是优化:两种循环的枚举
- 也就是枚举左端点l和右端点r的所有可能
- 优化关键就是:去除枚举中的冗余部分
具体优化策略
- 固定右端点,看左端点的取值范围
就是根据题意,把[j,i]范围中,j的这层循环去掉(j从0~i)
- 移动一个端点,观察另一个断点变化
就是滑动窗口,一个端点跟随另一个端点来移动
双指针解决两数之和
sort()函数
sort(first_pointer,first_pointer+n,cmp)
int a[8] = {6, 7, 2, 9, 1, 3, 5, 2};
sort(a, a + 8,less<int>());//less<数据类型>()
//默认从小到大,less<int>()可省略
int a[8] = {6, 7, 2, 9, 1, 3, 5, 2};
sort(a, a + 8,greater<int>());
//这是从大到小排列
注意:less<>()和greater<>()数据类型要写对
float f[5] = {11.2, 76.7, 8.32, 15.12, 2.676};sort(f, f+sizeof(f)/sizeof(float),less<double>());double d[5] = {1.2, 7.7, 8.32, 5.12, 2.66};sort(d, d + 5,greater<double>());
vector一样,而且传参可以传入自带的迭代器
vector<double> f= {11.2, 76.7, 8.32, 15.12, 2.676};sort(f.begin(),f.end(),less<double>());vector<float> d= {1.2, 7.7, 8.32, 5.12, 2.66};sort(d.begin(), d.end(),greater<double>());
自定义函数
sort()第三个参数可以自己自定义,注意函数要用bool返回值,而且传参时不要加()
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
struct student{string name;int age;student(string s,int a):name(s),age(a){}
};
//按姓名升序
bool cmp_name(const student& a,const student& b){return a.name < b.name;
}
//按年龄降序
bool cmp_age(const student& a,const student& b){return a.age > b.age;
}
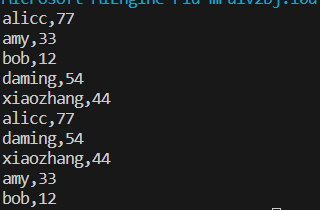
int main(){student stu[5] = {{"daming", 54},{"xiaozhang", 44},{"amy", 33},{"bob", 12},{"alicc", 77}};sort(stu, stu+5, cmp_name);for(auto [name,age]:stu){cout << name << "," << age << endl;}vector<student> vec(stu, stu + 5);//迭代器初始化sort(vec.begin(), vec.end(), cmp_age);for(auto [name,age]:vec){cout << name << "," << age << endl;}
}
数组指针初始化
vector vec(
stu + 1,stu + 4);
参数的函数无括号
sort(vec.begin(), vec.end(), cmp_age);
已排序数组的两数之和
167. 两数之和 II - 输入有序数组
利用排序特点,一端指向最小,一段指向最大。那么相加多了,大的减小,少了,小的增加。
vector<int> twoSum(vector<int>& numbers, int target) {//左右指针向中间移动int i=0;int j=numbers.size()-1;while(i<j){if(numbers[i]+numbers[j]>target){j--;}else if(numbers[i]+numbers[j]<target){i++;}else{//numbers[i]+numbers[j]==targetreturn {i+1,j+1};}}return {};}
法二:固定一端,考虑另一端的变化情况
vector<int> twoSum(vector<int>& numbers, int target) {//左右指针向中间移动int j=numbers.size()-1;for(int i=0;i<numbers.size();i++){//固定左端i,考虑j//只要大了,就一直移动jwhile(i<j && numbers[i]+numbers[j]>target) j--;if(i<j && numbers[i]+numbers[j]==target){return {i+1,j+1};}//这里左端自己移动,所以小了不做考虑}return {};}
这里{
i+1,j+1}是题目要求从1开始只有:
i<j这个下标才有意义,所以要加入判断或者在代码写:if(i>=j) break;
未排序数组两数之和
1. 两数之和
采用自定义类型来存储原数组下标,然后排序
注意自定义类型的访问名称是类型的变量名称
vec[i].valvec[i].index
- 这里cmp函数需要加上static关键字
class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {int n = nums.size();vector<item> vec;for (int i = 0; i < n; i++) {//用vec存储排序前的下标vec.push_back(item(nums[i], i));}sort(vec.begin(),vec.end(),cmp);int j = n - 1;for (int i = 0; i < n; i++) {while (i < j && vec[i].val + vec[j].val > target)j--;if (i < j && vec[i].val + vec[j].val == target) {return {vec[i].index, vec[j].index};}}return {};}private:struct item {int val;int index;item(int v, int i) : val(v), index(i) {}};static bool cmp(const item& a, const item& b) { return a.val < b.val; }
};
或者直接用现成的pair,注意first和second是pair的成员
vector<int> twoSum(vector<int>& nums, int target) {//用pair来存储vector<pair<int, int>> vec;for(int i=0;i<nums.size();i++){vec.push_back(make_pair(nums[i],i));}sort(vec.begin(),vec.end());//默认排序k,v中kint j=nums.size()-1;//注意,这里访问的是已排序的vecfor(int i=0;i<vec.size();i++){while(i<j && vec[i].first+vec[j].first>target){j--;}if(i<j && vec[i].first+vec[j].first==target){return {vec[i].second,vec[j].second};}}return {};}
三数之和
15. 三数之和
双指针法的优势就是可以找到所有可能解,因为排序后的数组只要一大一小向中间移动,就会找到多个解
vector<vector<int>> colTwoSum(vector<int> &nums, int target){vector<vector<int>> res;int k = nums.size() - 1;for (int j=0; j < nums.size(); j++){while (j < k && nums[j] + nums[k] > target)k--;if (j < k && nums[j] + nums[k] == target){//只存不return,会找到所有结果res.push_back({nums[j], nums[k]});}}return res;
}
int main(){vector<int> nums = {1, 3, 4, 5, 6, 7, 8};auto res = colTwoSum(nums, 9);for(auto v:res){cout << v[0] << " " << v[1] << endl;}
}
/*
1 8
3 6
4 5*/
三数之和就是在两数之和基础上改进,关键:nums[j]+nums[k]==-nums[i],所以就是遍历i然后利用双指针的两数之和找到所有满足的j,k,然后把当前i并入结果即可
- 注意j从i+1开始,这样i,j,k就都不相同,且:i<j<k
- 注意:排序后的值:[1,1,2,2,3,3],i如果是一个数的话,同一个j,k会重复,所以相同的i值只判断一个
- 同理:j,k也要去重,j只选择不同的值。
- 最后数组下标一定要有意义,所以合法性检查不可少
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {//题目要求返回值,所以可以直接排序sort(nums.begin(),nums.end());//遍历nums[i],向后找:nums[j]和nums[k]//即:nums[j]+nums[k]==-nums[i](保证i,j,k不同)vector<vector<int>> ans;for(int i=0;i<nums.size();i++){//去重if(i>=1 && nums[i]==nums[i-1]) continue;auto res=colTwoSum(nums,i+1,-nums[i]);//所有的res结果并入nums[i]for(auto v:res){ans.push_back({nums[i],v[0],v[1]});}}return ans;}
private:vector<vector<int>> colTwoSum(vector<int>& nums,int j,int target){vector<vector<int>> res;int k=nums.size()-1;int tmp=j;for(;j<nums.size();j++){if(j>tmp && nums[j]==nums[j-1]) continue;while(j<k && nums[j]+nums[k]>target) k--;if(j<k && nums[j]+nums[k]==target){res.push_back({nums[j],nums[k]});}}return res;}
};
也可以不写函数:
vector<vector<int>> threeSum(vector<int>& nums) {//题目要求返回值,所以可以直接排序sort(nums.begin(),nums.end());//遍历nums[i],向后找:nums[j]和nums[k]//即:nums[j]+nums[k]==-nums[i](保证i,j,k不同)vector<vector<int>> ans;for(int i=0;i<nums.size();i++){//去重if(i>=1 && nums[i]==nums[i-1]) continue;int k=nums.size()-1;//类似函数传参,初始值定义在外面int target=-nums[i];for(int j=i+1;j<nums.size();j++){if(j>i+1 && nums[j]==nums[j-1]) continue;while(j<k && nums[j]+nums[k]>target) k--;if(j<k && nums[j]+nums[k]==target){//直接装入ans.push_back({nums[i],nums[j],nums[k]});}}}return ans;}
双指针,容器盛水
11. 盛最多水的容器
解题关键就是意识到:面积是由短板和距离决定,如果距离最长,那面积完全取决于短板
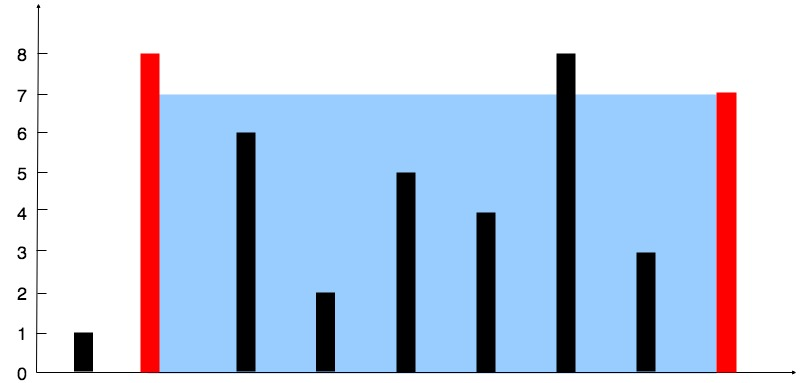
- 距离一定,长板不动,移动短板,面积可能变大
- 距离一定,短板不动,移动长板,因为短板是固定的,面积一定不会增大
所以每次计算面积后,移动最短的那块板
这里i,j两端变化无规律,取决于height[i]和height[j],用while最合适
int maxArea(vector<int>& height) {int res=0;//双指针int i=0,j=height.size()-1;while(i<j){//不可以相遇res=max(res,min(height[i],height[j])*(j-i));//谁短移动谁if(height[i]<height[j]) i++;else j--;}return res;}
res=height[i]<height[j]?max(res,(j-i)*height[i++]):max(res,(j-i)*height[j--]);注意:因为自增自减,不可以用:height[i++]*(j-i);
单调栈
单调递增堆栈是指元素从下到上按升序排列的堆栈
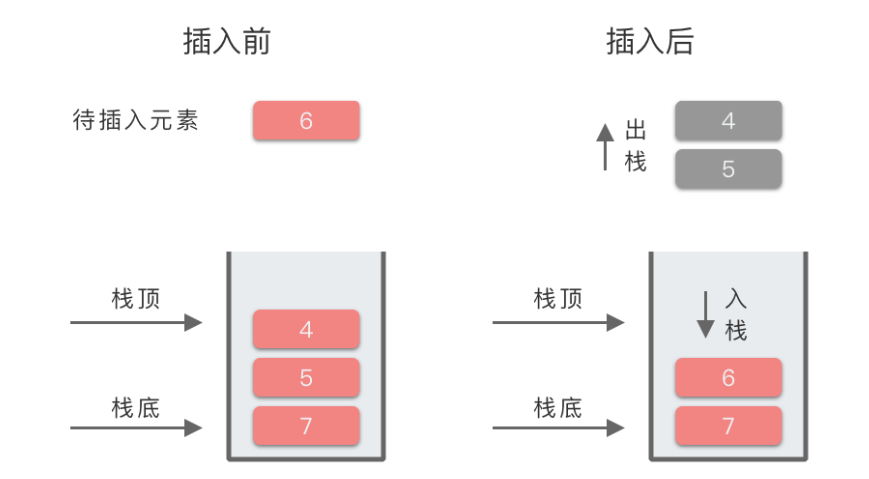
单调递减堆栈是元素从底部到顶部按降序排列的堆栈
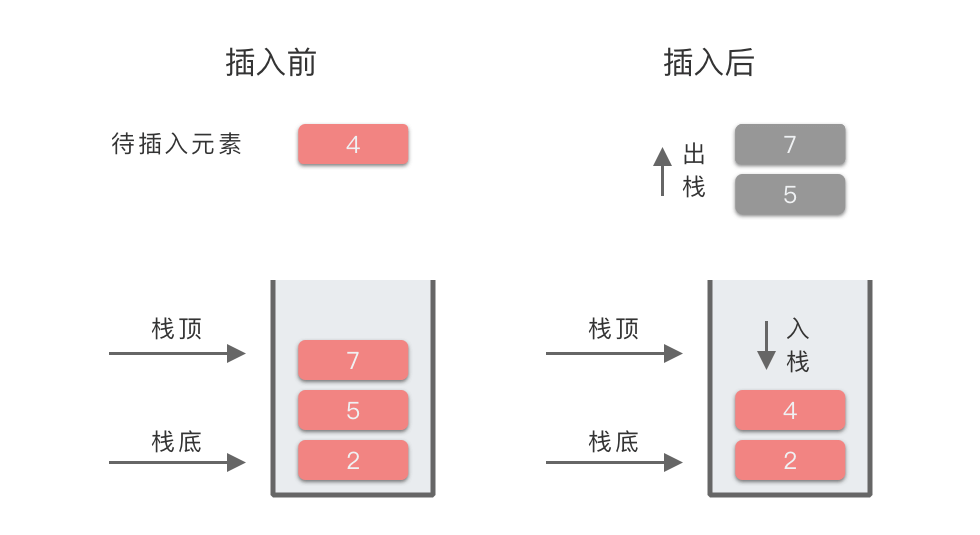
实现单调递增栈
//栈顶元素最大,而且出栈大小依次递减
考虑一个数组 Arr[] = {1, 4, 5, 3, 12, 10}
对于 i = 0: stk = {1}
对于 i = 1: stk = {1, 4}
对于 i = 2: stk = { 1, 4, 5}
对于 i = 3: stk = {1, 3} [弹出 4 和 5 作为 4 > 3 和 5 > 3]
对于 i = 4: stk = {1, 3, 12}
对于 i = 5 : stk = {1, 3, 10} [将 12 弹出为 12 > 10]
class monoStack{
public:/*单调递增栈*/void increase_stack(vector<int> vec){//初始化一个栈,存下标stack<int> sta;//访问每一个元素for (int i = 0; i < vec.size();i++){//新元素一定会入栈,但是必须把大于它的值出栈while(!sta.empty()&& vec[i]<vec[sta.top()]){sta.pop();}//入栈sta.push(i);}//把单调栈出栈,把结果存入resres.resize(sta.size());for (int j = sta.size() - 1; j >= 0;j--){res[j] = vec[sta.top()];sta.pop();}}
private:vector<int> res;
};
int main(){vector<int> a{1, 4, 5, 3, 12, 10};monoStack ms;ms.increase_stack(a);
}
递减单调栈(栈底元素最大,栈顶元素最小)
void decrease_stack(vector<int> vec){//递减,栈底元素最大stack<int> sta;for (int i = 0; i < vec.size();i++){//入栈前,必须去掉栈中比自己小的while(!sta.empty()&&sta.top()<vec[i]){sta.pop();}sta.push(vec[i]);//存入值}//把单调栈结果存入resres.resize(sta.size());for (int i = sta.size() - 1; i >= 0;i--){res[i] = sta.top();sta.pop();}}
应用~计算直方图内最大矩形面积
84. 柱状图中最大的矩形
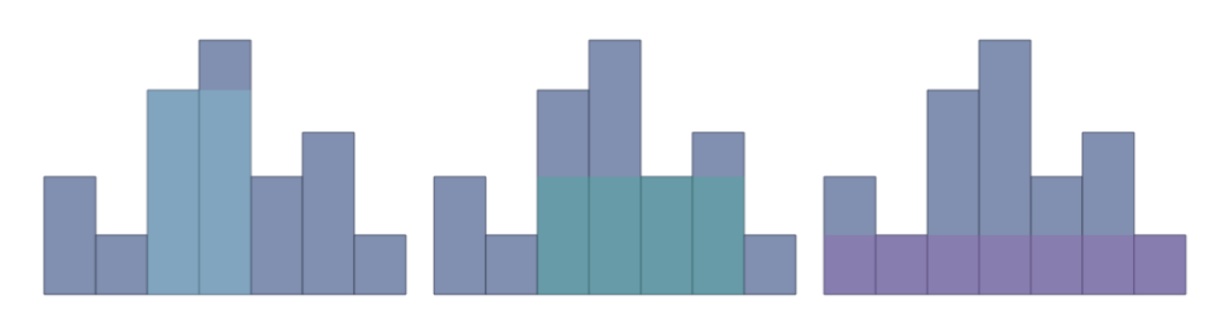
题目特点就是:可延伸,是直方图内部的构成的最大面积
如果用暴力解法:
+ 左右指针初始化为当前柱子i,高度:heights[i]
+ 只要两端左边或右边比heght[i]小就是可延伸
+ 也就是:从中心向两端扩散
int largestRectangleArea(vector<int>& heights) {int n=heights.size();int res=0;for(int i=0;i<n;i++){int left=i;int right=i;int h=heights[i];while(left>=0 && heights[left]>=h) left--;/*for(;left>=0;left--)if(heghts[left]<h) break;*/while(right<n && heights[right]>=h) right++;int w=right-left-1;//延伸宽度:(left,right)res=max(res,w*h);}return res;}
应用单调栈
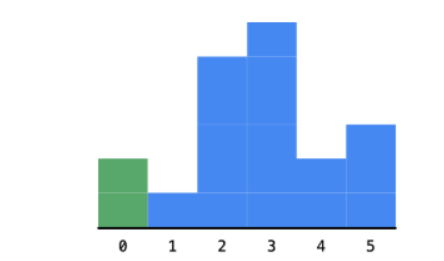
特点就是:每次遍历柱子的时候,如果当前柱子高度比他的前一个柱子矮的话(比如:1比0矮)
此时:前一个柱子高度一定不能向后扩展,所以会计算出以它的高度可能向前延申的面积
这里的123是严格递增的,所以此时他们各自高度形成最大面积不能判断,因为可能会向后延申
也就是说,每次我们都把单调不减的柱子放入单调栈,万一当前柱子比栈顶元素高度小,那么就出栈,可以计算出它的面积了
问题关键就是:向前延申的面积的宽度怎么确定?
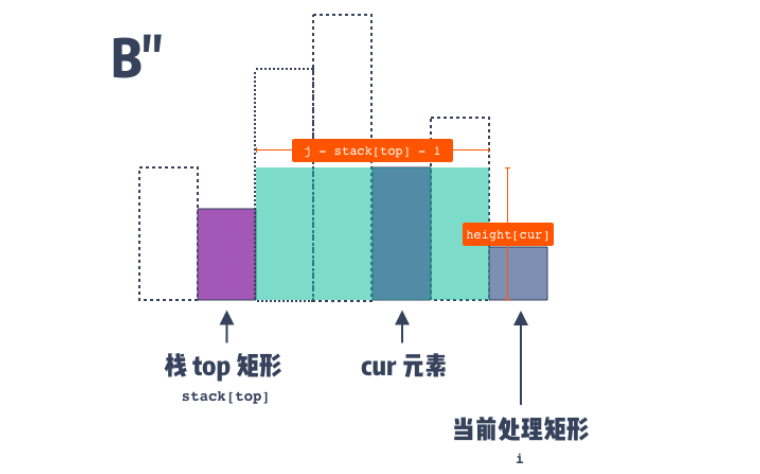
就是:当前出栈元素高度height[sta.top()],出栈后,当前访问访问柱子i和单调栈栈顶元素之间的宽度
也就是:i-栈top()位置-1
因为:我们维持一个单调递增的单调栈,如果柱子i比栈顶小,那么前一个一定可以计算出面积。
而它延申的最长距离就是出栈后的单调栈栈顶位置(因为严格单调递增一定延申不到这个位置)
注意到,访问最后一个元素后没有结束,所以需要再加入一个小值,以便把整个栈内元素出栈
int largestRectangleArea(vector<int>& heights) {int n=heights.size();int res=0;stack<int> sta;for(int i=0;i<=n;i++){//为了让最后一个元素能出栈,不妨让n时直方图高度-1//-1会保证单调栈内所以元素出栈int curHeight=(i==n)?-1:heights[i];/*单调栈模板:先把破坏单调性元素出栈,然后必入栈*/while(!sta.empty() && curHeight<=heights[sta.top()]){//i-1位置的面积可求int h=heights[sta.top()];sta.pop();//计算面积后就不存了//因为sta.top()在栈空时不存在int w;//宽度if(!sta.empty()) w=i-sta.top()-1;else w=i;//0 1 .. 这根柱子(i-1) i---(i-1)-0+1res=max(res,w*h);}sta.push(i);//必入栈}return res;}
curHeight<=heights[sta.top()]这里考虑了相等柱子不入栈,跟测试用例有关,写<也行
if(!sta.empty()) w=i-sta.top()-1;
else w=i;//0 1 .. 这根柱子(i-1) i---(i-1)-0+1由于递减形状可能会让栈没元素,注意:sta.top()的存在前提是栈不空
哨兵
单调栈需要考虑两种特殊的情况:
- 弹栈的时候,栈为空;
- 遍历完成以后,栈中还有元素;
在输入数组的两端加上两个高度为 0的柱形,可以回避上面这两种分类讨论。
这两个站在两边的柱形有一个很形象的名词,叫做哨兵(Sentinel)
有了这两个柱形:
左边的柱形(第 1 个柱形)由于它一定比输入数组里任何一个元素小,它肯定不会出栈,因此栈一定不会为空;
右边的柱形(第 2 个柱形)也正是因为它一定比输入数组里任何一个元素小,它会让所有输入数组里的元素出栈(第 1 个哨兵元素除外)。
int largestRectangleArea(vector<int>& heights) {//在原来直方图前后两端各加一个0//右端的0会让单调栈全部出栈//左端的0会让单调栈不为空heights.insert(heights.begin(),0);heights.insert(heights.end(),0);int res=0;stack<int> sta;for(int i=0;i<heights.size();i++){while(!sta.empty() && heights[i]<heights[sta.top()]){int h=heights[sta.top()];sta.pop();int w=i-sta.top()-1;res=max(res,h*w);}sta.push(i);}return res;}

)








容器化部署传统应用(Redis+Postgresql+Git+SpringBoot+Nginx))

![洛谷 P1087 [NOIP2004 普及组] FBI 树](http://pic.xiahunao.cn/洛谷 P1087 [NOIP2004 普及组] FBI 树)







