1 介绍
- 精准最近邻搜索中数据维度一般较低,所以会采用穷举搜索,即在数据库中依次计算其中样本与所查询数据之间的距离,抽取出所计算出来的距离最小的样本即为所要查找的最近邻。
- 当数据量非常大的时候,搜索效率急剧下降。
- ——>近似最近邻查找(Approximate Nearest Neighbor Search,简称 ANN)是一种在大规模数据集中查找与给定查询点最相似(或“最近”)的数据点的优化算法。
- 与精确最近邻查找不同,近似最近邻查找不保证找到绝对最近的邻居,但它通常比精确方法更快,尤其是在高维数据空间中。
- 在牺牲可接受范围内的精度的情况下提高检索效率
- 近似最近邻检索利用数据量增大后数据之间会形成簇状聚集分布的特性,通过对数据分析聚类的方法对数据库中的数据进行分类或编码,对于目标数据根据其数据特征预测其所属的数据类别,返回类别中的部分或全部作为检索结果。
2 KD 树
算法笔记:KD树_UQI-LIUWJ的博客-CSDN博客
3 球树
算法笔记:球树_UQI-LIUWJ的博客-CSDN博客
- KD树和球树通常用于精确最近邻查找,但也可以用于近似最近邻查找
-
限制搜索深度
- 在构建KD树/球树的过程中,每个节点都会分割其包含的数据点。在查找最近邻时,通常会遍历这些节点以找到最近的点
- 通过限制搜索深度,可以减少搜索时间,但这可能会导致找到的点不是真正的最近邻
-
早停准则
-
在搜索过程中,一旦找到一个与查询点距离在某个阈值范围内的点,就停止搜索。
-
这样可以加速查找过程,但可能会错过更近的点。
-
-
4 LSH 局部敏感哈希(locality-sensitive hashing)
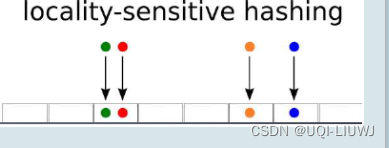
- LSH的基本思想是将相近的点映射到相同或相近的“桶”(bucket)中,以便能快速地检索这些点。
4.1 几个概念
-
哈希函数族:
- 选择一个局部敏感的哈希函数族,该函数族具有一个重要的性质:距离近的点被哈希到相同桶的概率高,而距离远的点被哈希到相同桶的概率低。
-
局部敏感
- 一个局部敏感的哈希函数族 H 对于任意两个点 p 和 q,以及任意两个距离阈值 R 和 r(R>r),具有以下性质
-
正性质: 如果 distance(p,q)≤r,则 h(p)=h(q) 的概率较高。
-
也就是说,如果两个点 p 和 q 距离很近,那么它们被哈希到同一个桶的概率应该很高。
-
-
负性质: 如果distance(p,q)≥R,则 h(p)=h(q) 的概率较低。
-
也就是说,如果两个点 p 和 q 距离很远,那么它们被哈希到同一个桶的概率应该很低。
-
-
- 一个局部敏感的哈希函数族 H 对于任意两个点 p 和 q,以及任意两个距离阈值 R 和 r(R>r),具有以下性质
-
多哈希表:
- 通常使用多个这样的哈希表,以增加查找精度。
-
候选集生成:
- 对于一个查询点,首先计算其哈希值,并在相应的桶中查找候选点。
-
后处理:
- 在候选集中进行距离计算,以找到最近邻




)

)
)

事务----》数据库运行的原理知识+面试题~)





)



