Merging of neural networks

论文链接：https://arxiv.org/pdf/2204.09973v2.pdf
源码链接：https://github.com/fmfi-compbio/neural-network-merging

简介

典型的神经网络训练从随机初始化开始，并进行训练，直到在某些局部最优中达到收敛。最终结果对开始的随机种子非常敏感。因此，人们可能要多次进行实验以避免碰到不幸种子。最终选择的网络正是具有最佳验证精度的实验。
本文认为启动种子之间的差异可能通过在每次初始化中在隐藏层中选择稍微不同的特征来解释。人们可能会有一个问题，能以某种方式为网络训练选择更好的特征？一种方法是训练更大网络然后通过通道剪枝选择最重要通道。在许多情况下，训练一个随后被剪枝的大网络可能是令人望而却步的，因为将网络宽度增加两倍会导致FLOPs增加4倍，并且还可能需要改变一些超参数。
在这里本文提出一种替代方法。本文将训练两个相同大小的网络并将其合并为一个网络，而不是训练一个更大的网络并对其进行剪枝。思想是每个训练运行都会陷入不同的局部最优，因此在每一层中都有不同的滤波器集合。然后，本文可以选择一组比原始网络更好的滤波器，并获得更好的精度。

本文方法

本文训练策略包括三个阶段：

训练两个教师，
融合流程：创建一个学生包含如下字步骤：
a) 教师逐层连接成一个大学生模型，
b) 学习大学生模型神经元重要性，
c) 大学生模型压缩。
大学生模型微调。
教师的训练和学生模型的微调只是通过反向传播对神经网络的标准训练。后文描述如何从两个教师那里获得一个学生模型。

把教师模型层层连接为一个大学生模型

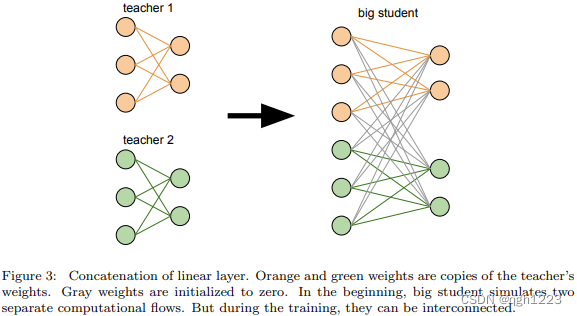
大学生模型墨迹两个教师模型并在最后一层对他们预测进行平均。这个阶段只是网络转换没有任何训练。如图3所示。卷积层的合并是在通道维度上进行的。线性曾的连接时在特征维度中类似完成的。本文将这个模型称为大学生模型，因为他的宽度是原来的两倍。
在这里插入图片描述

大学生模型神经元的学习重要性

本文希望大学生模型会在每层只使用一半的神经元。因此，在去除了不重要神经元后，将使用原始架构。除了学习神经元相关性，还希望这两个计算流相互连接。
有多种方式寻找最相关通道。可以将分数分配给各个通道，也可以使用辅助损失指导网络选择最相关通道。本文选择后者方法。它利用L0损失。
定义 $\ell$ 是有k输入特征的线性层。 $g_{i}$ 是分配给 $f_{i}$ 的门。门可以是开 $g_{i}=1$ （学生使用特征）或关 $g_{i}=0$ （学生不使用特征）。在计算层的输出前，首先将输入乘以门，既不是计算 $W f + b$ ，而是计算 $W(f\cdot g)+b$ 。为了使本文模型只是用想要一半特征想要满足 $\frac{1}{n}\sum_{1}^{k}g_{k}=\frac{1}{2}$ 。
该方法问题是 $g_{i}$ 是离散的，不能使用梯度下降训练。为了克服这个问题，本文使用Learning sparse neural networks
through l_0 regularization中随机门和 $L_{0}$ 连续松弛。随机门包含概率为0的非0随机变量： $P[g_{i}=0]>0$ ，非0概率为1 $P[g_{i}=0]>1$ 。重参数化技巧使得门分布可由梯度下降训练。
为了鼓励大学生模型只使用层的一半特征，使用一个辅助损失：
$L_{half}^{\ell}=(\frac{1}{2}-\frac{1}{k}\sum_{1}^{k}P[g_{i}>0])^{2}$
尽管本文损失函数迫使模型恰好打开一半的门，但它们损失促使模型使用尽可能少的门。
因此本文优化 $L=L_{E}+\lambda\sum_{l}L_{half}^{\ell}$ 。其中 $L_{E}$ 是数据集上误差损失测量拟合，新的超参数 $\lambda$ 是误差损失和辅助损失重要性比例。
超参数 $\lambda$ 很敏感，需要适当调整。在训练开始时，不能太大，否则学生会以概率为0.5将每个门设置为关闭。在训练结束时，不能太小，否则学生会忽视辅助损失，又例如误差损失。他将使用该层一半以上神经元，并在压缩后显著降低性能。
本文在一个单独的层中实现了门。使用两个门层设计，一个用于二维双通道另一个用于一维通道。门层位置至关重要。例如如果门层正好位于BatchNorm之前，其效果（将通道乘以0.1）将被BatchNorm抵消。