目录
材质
漫反射
镜面反射
折射-Snell’s Law
Fresnel Reflection / Term(菲涅耳项)
微表面模型
各向同性与各向异性
BRDF的性质
测量BRDF
材质
渲染方程中的BRDF描述了物体是如何与光线作用的,而物体的材质决定了它看起来是怎么样的,也就是它的材质决定了光线是如何反射的,即BRDF就表示了物体的材质这个属性
漫反射
Diffuse / Lambertian Material,即漫反射,如果是漫反射,那么物体接收到的光和物体漫反射出去的光应该是一样的,那BRDF和漫反射光就应该是一个常数,假设物体本身不发光,那么渲染方程可以写成下面的式子,并且假设物体不吸收光,那么Lo和Li应该相等,这样就可以算出BRDF,也就是漫反射系数等于1/,那实际上物体是会吸收光的,所以还需要乘上一个系数ρ,这个系数ρ的范围在[0,1]之间
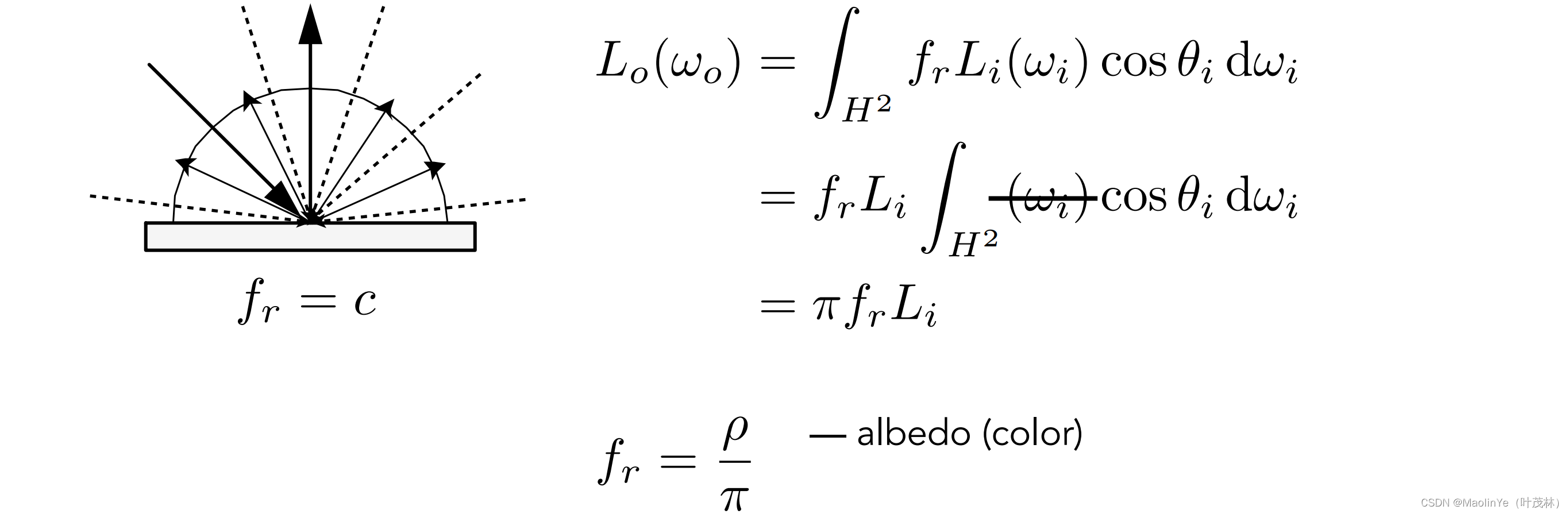
镜面反射
那镜面反射我们怎么确定这个反射的方向呢?
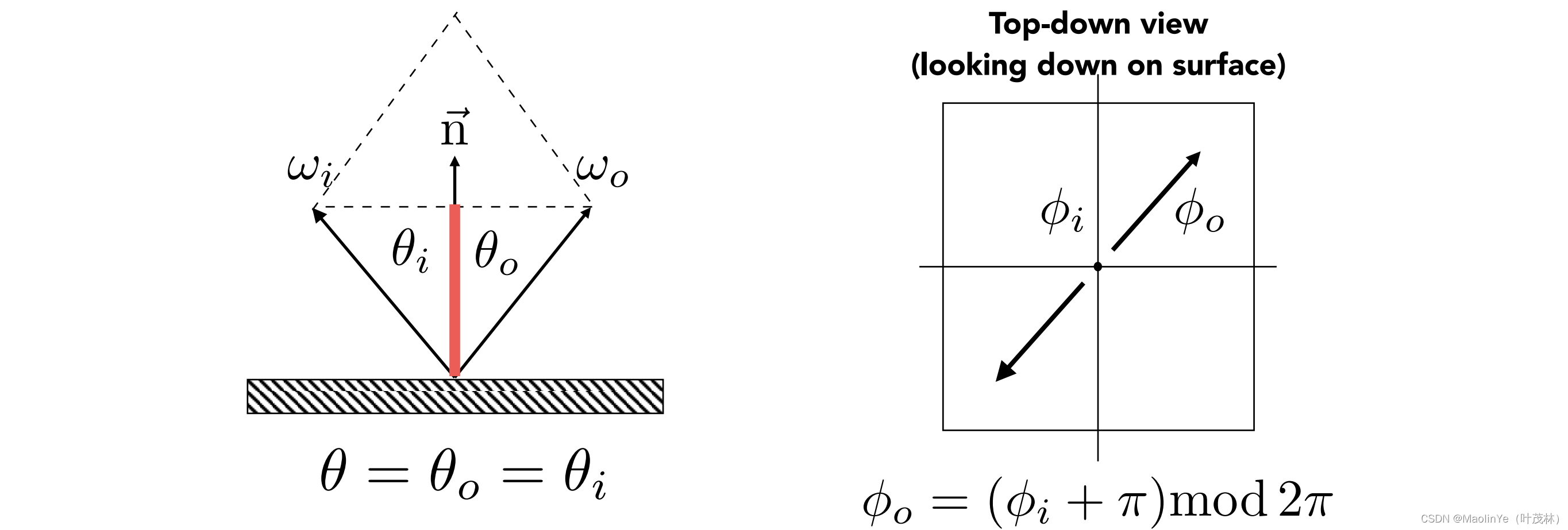
我们说三维中的一个角,叫这个空间角,实际上可以表示为和竖直方向n的一个夹角w和与水平方向的一个夹角,这个w好算,因为镜面反射那入射角等于发射角,也就是wo+wi等于2倍的红色部分,而这个红色部分方向和n一样,大小是这个w在n的投影,所以是w和n做一个点乘的结果,因为方向向量都是单位向量,点乘的结果就等于余弦值,所以这个w可以算出来,而这个与水平方向的夹角
就是从上往下俯视看,入射方向和反射方向是相反的,所以这个
o就等于
i+
再和2
取余的结果
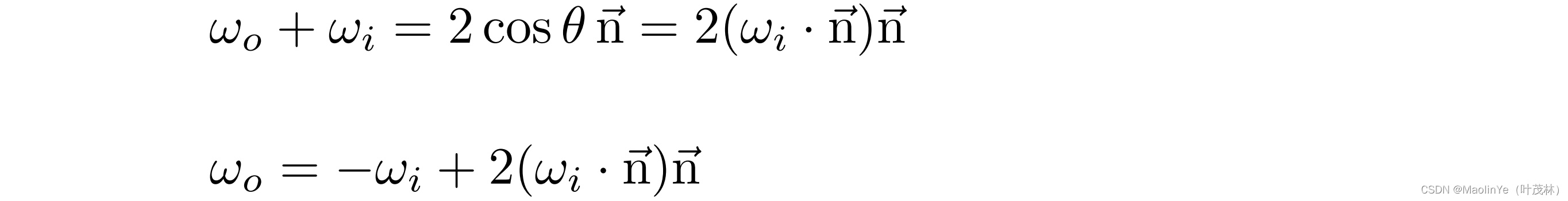
折射-Snell’s Law
对于折射的方向(,
),唉这个折射的水平夹角
还是和刚刚镜面反射一样在同一平面方向相反,入射和折射的
就差一个
,那这个
怎么算,有这么一个Snell’s Law,叫斯涅尔定律,就是说
i
i=
t
t,就是介质的折射率
和
的正弦值的乘积是不变的
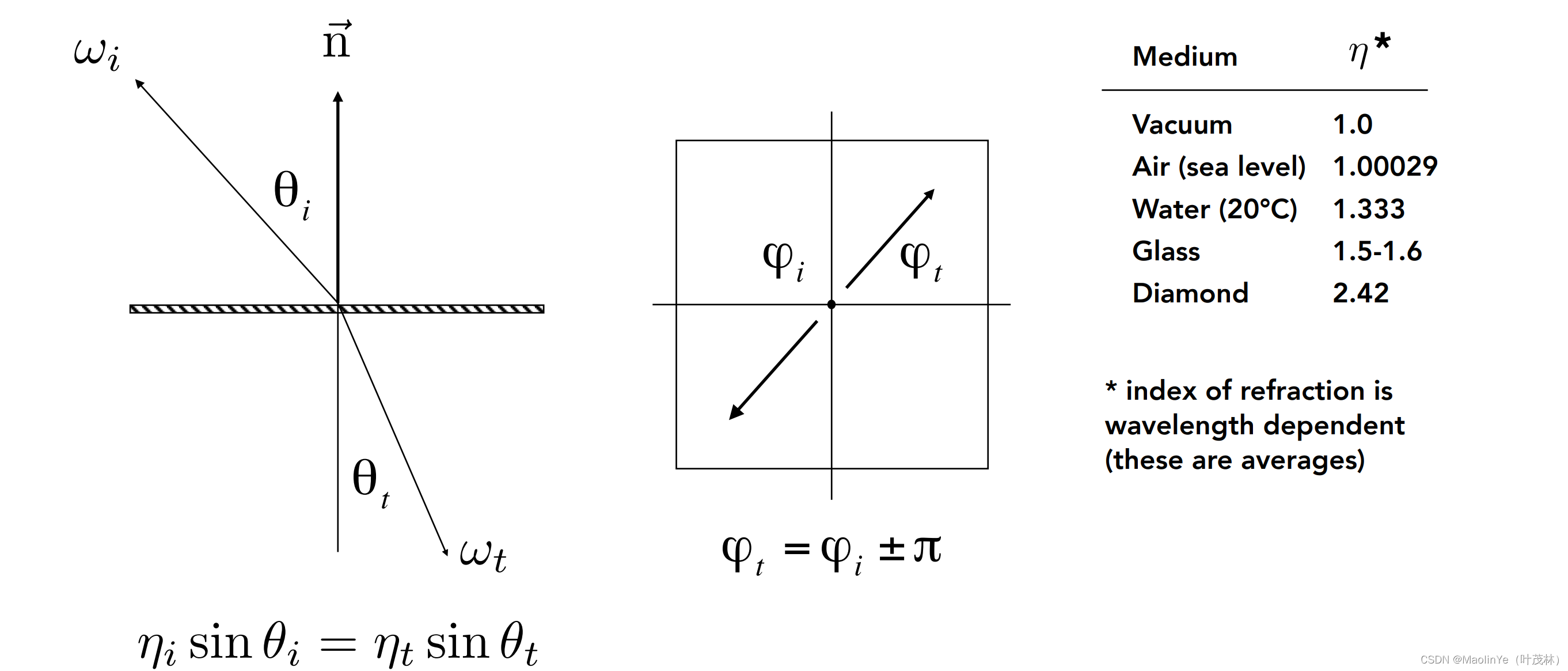
由这个等式可以算出这个折射角t的余弦值,这个要求有意义的话那么根号里面的项就得非负,也就是这个乘积部分必须得小于等于1,那后面减法部分不可能大于1,只有
i比
t大,那这个式子才会没有意义,此时折射就不会发生了,即入射介质的折射率大于折射介质的折射率
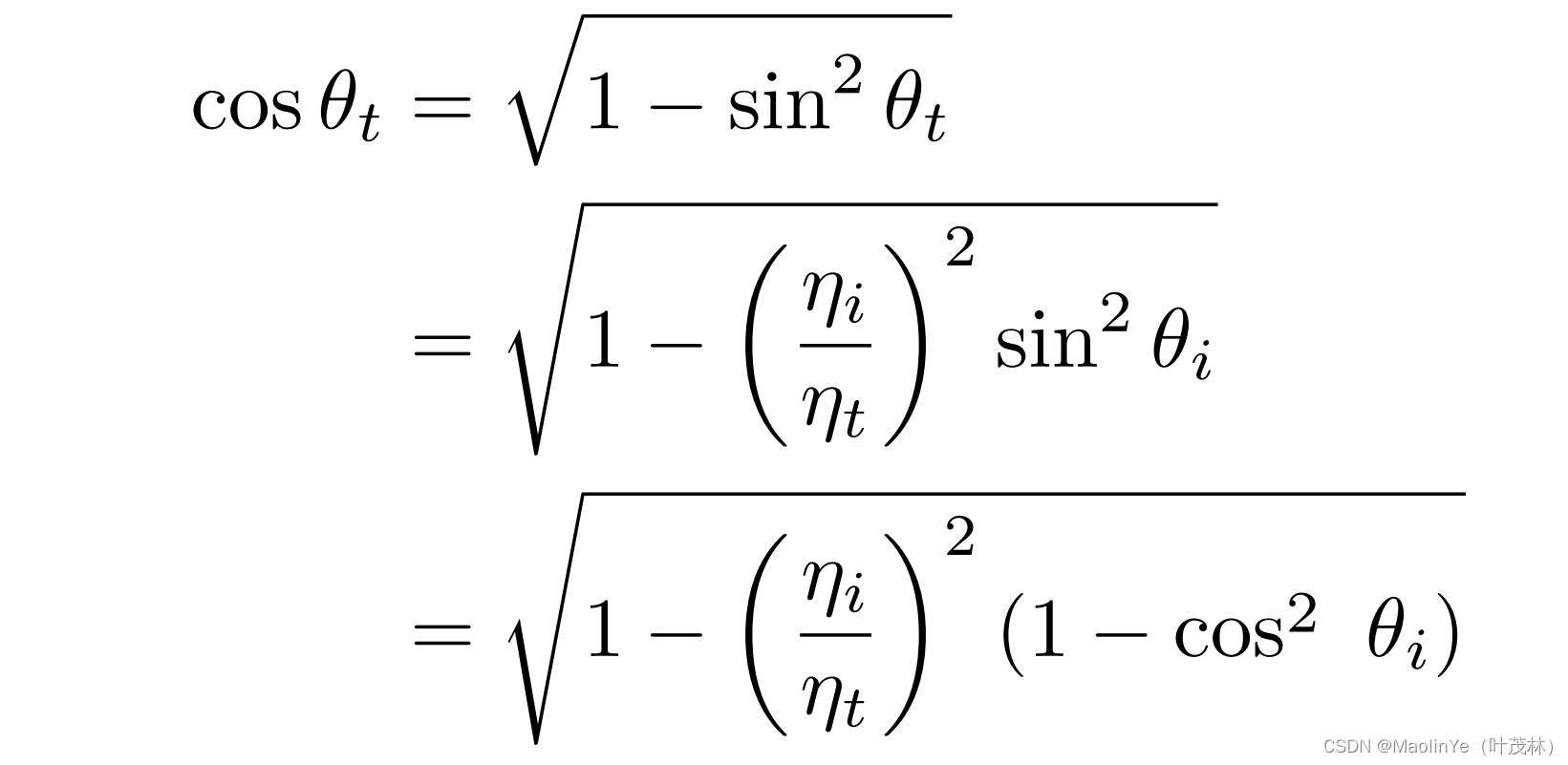
BRDF不是双向发射分布函数吗,这个折射就叫BTDF,T是transmit,折射和反射统称散射scattering,即BSDF=BRDF+BTDF
Fresnel Reflection / Term(菲涅耳项)
菲涅耳项是用来描述光在不同折射率的介质之间的行为的,说的是有多少能量会被反射,有多少能量会被折射,当入射角很小的时候(垂直照射物体),折射很多,反射很少,当入射角很大(平行照射物体)时,反射很多,折射很小
还有就是导体和绝缘体的菲涅耳项不太一样,导体的反射很强,即使入射角很小也会有很多能量反射,这也是为什么镜子用银镜、铜镜
那怎么算呢,有比较复杂的式子计算,这个S和P是两个极化方向,所谓极化就是光线只沿着某个方向震动,那不极化的就把Rs和Rp平均一下
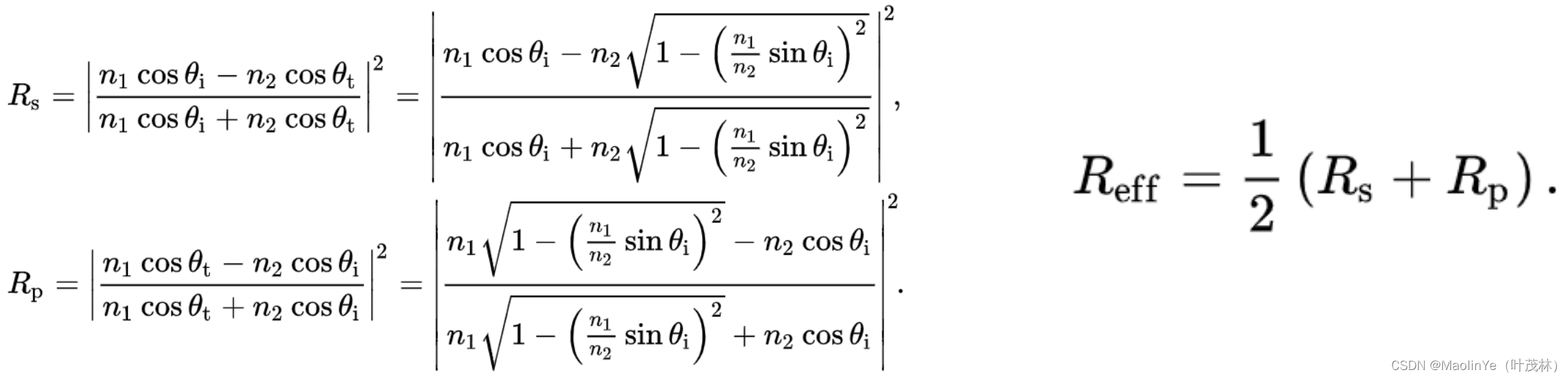
但是呢还有一个简化的计算,那反射强度不都是在垂直的时候最小平行的时候最大么,那我先算出一个最小的R0,这个和两边的折射率有关系,然后我用一个式子去描述这个发射强度随入射角的变大而变大这么一种关系
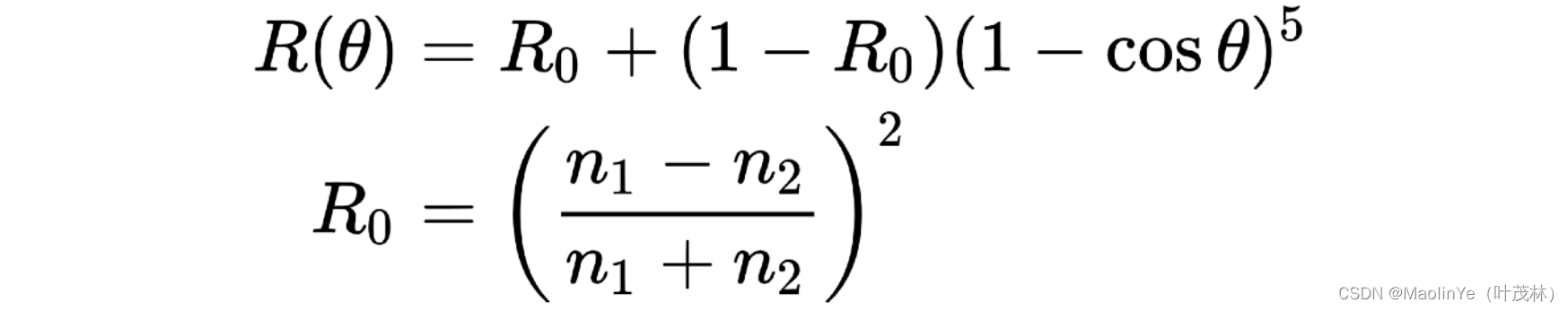
微表面模型
对于一个物体的表面,我从远处或者是宏观上看到的是这个物体的材质,从微观上看到的是这个物体表面的几何信息
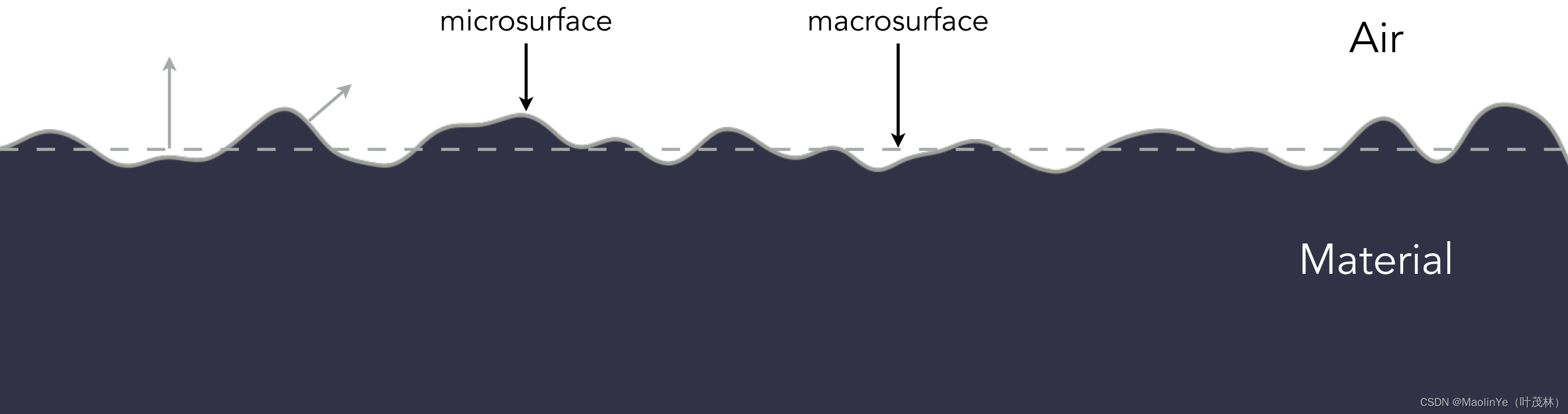
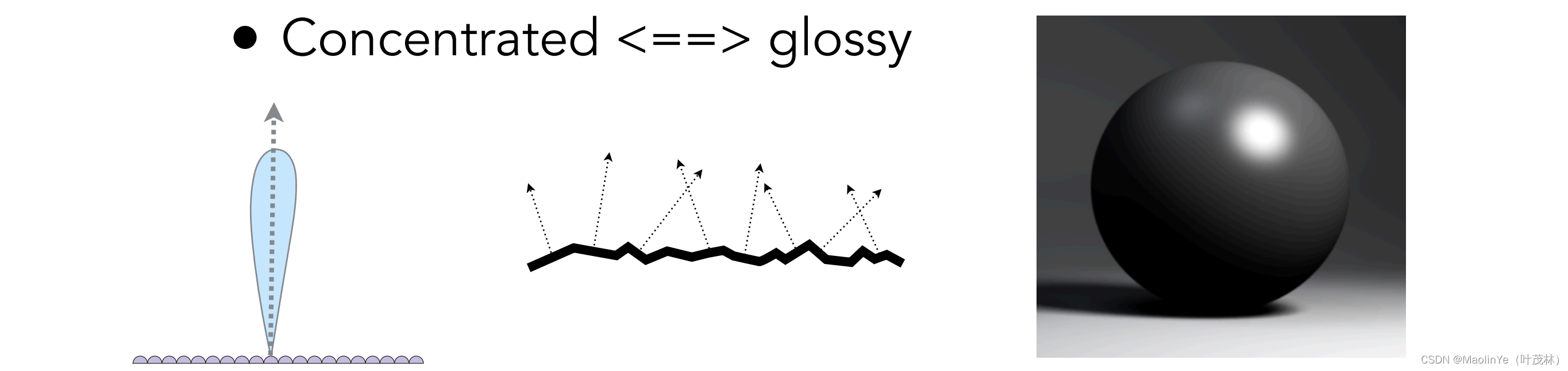
对于物体表面的微小平面可以认为是完全镜面反射的,如果这些微小平面的法线方向比较集中的话,就是glossy材质
如果这些微小平面的法线方向比较分散的话,就是漫反射
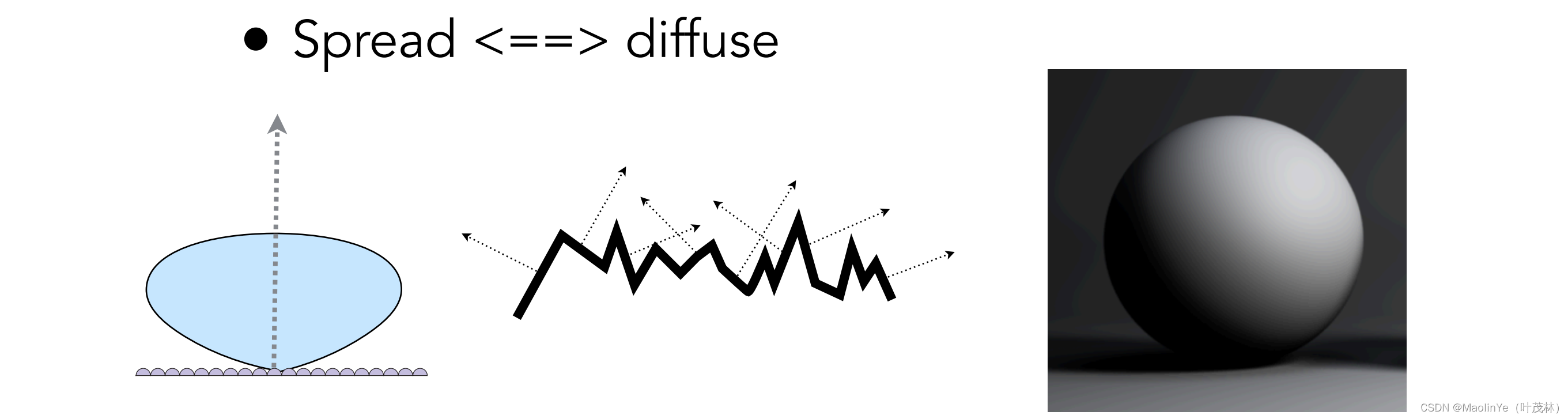
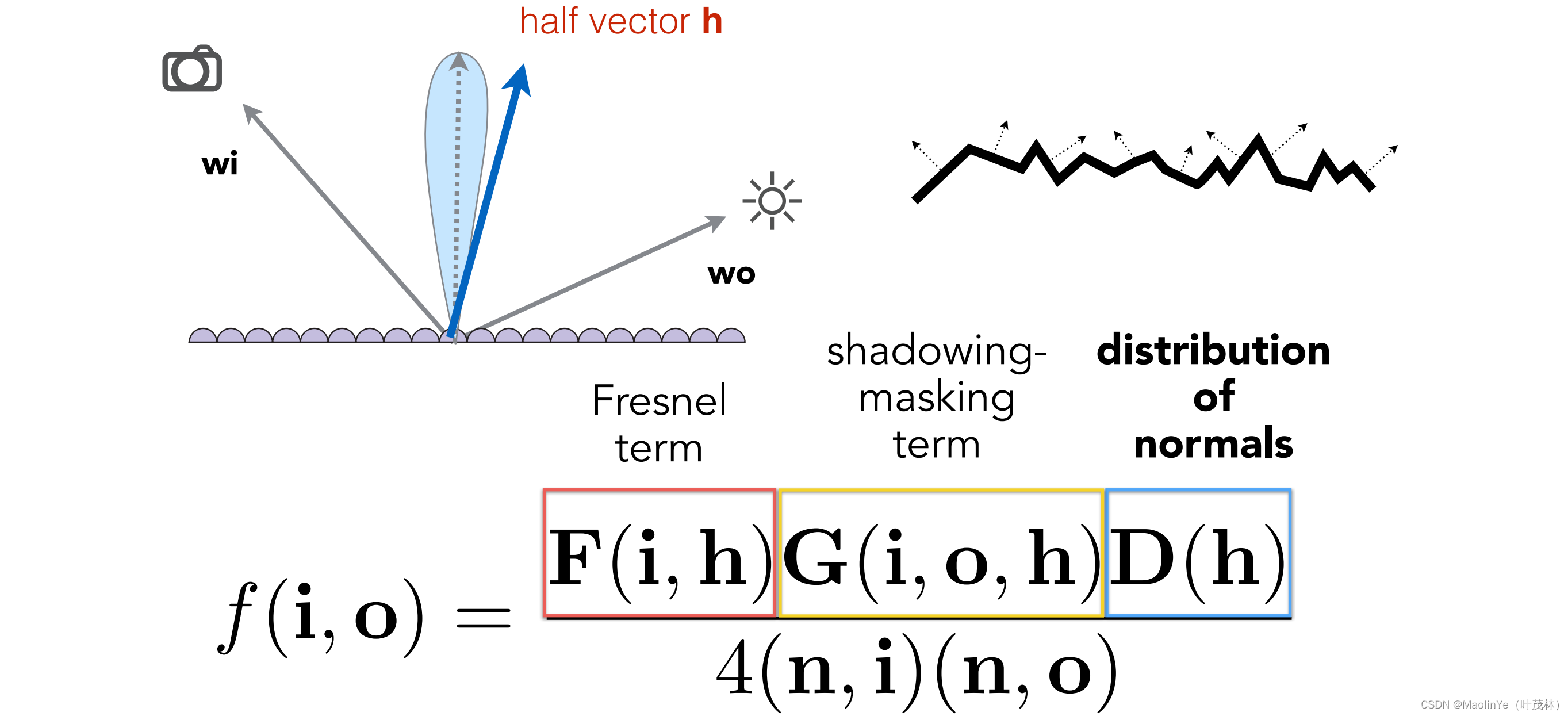
所以这个微表面模型可以通过法线方向的集中程度来描述物体表面的粗糙程度,那这个微表面的BRDF怎么算呢,可以看到有这三项F、G和D,这个F就是菲涅耳项,D呢是描述微表面的法线的分布,还记得blinn-phone模型里面计算高光的时候用到的半程向量h,那只有这个法线方向和半程向量方向一致的时候才能反射出来,还有这个G是为了解决这个微表面相互遮挡的问题,就是当光线平行照射微表面的时候,这个入射角叫grazing angle,如果没有G修正那么边界就会很亮
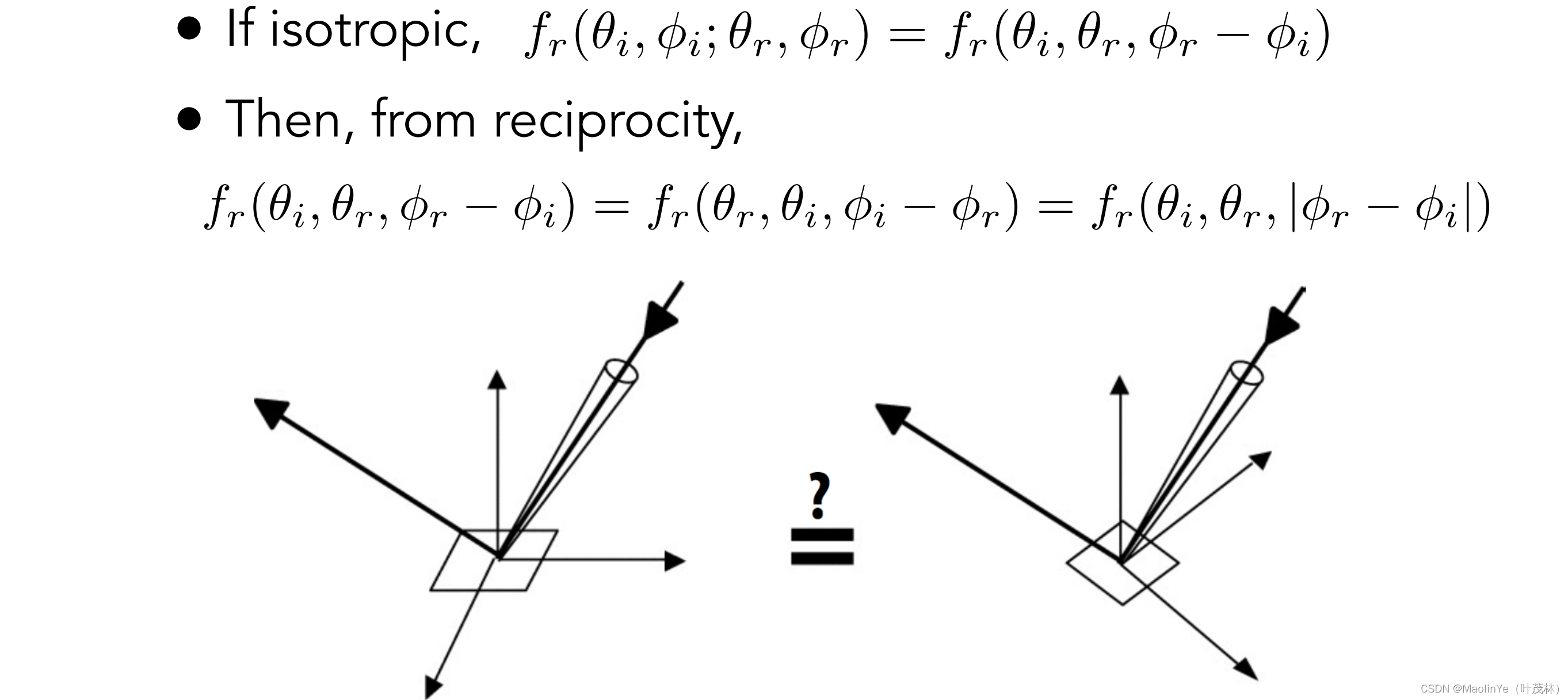
各向同性与各向异性
Isotropic(各向同性)的微表面法线分别比较均匀,而Anisotropic(各向异性)的微表面法线分布具有一定的方向性

反映在BRDF上,就是入射方向和反射方向沿着水平旋转不会改变BRDF的话那就是各向同性的,否则就是各向异性的,即各向同性的BRDF只和相对的水平角有关系

BRDF的性质
非负
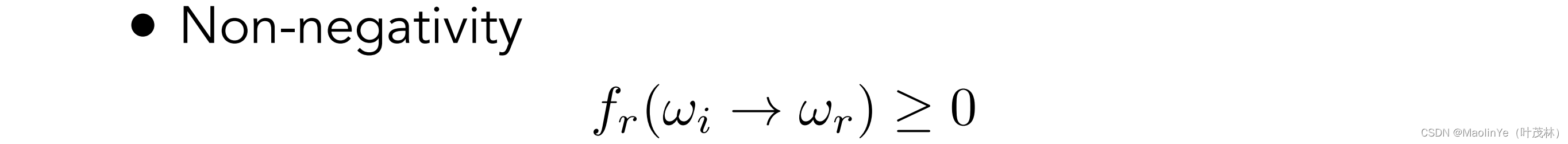
线性可加

可逆相同
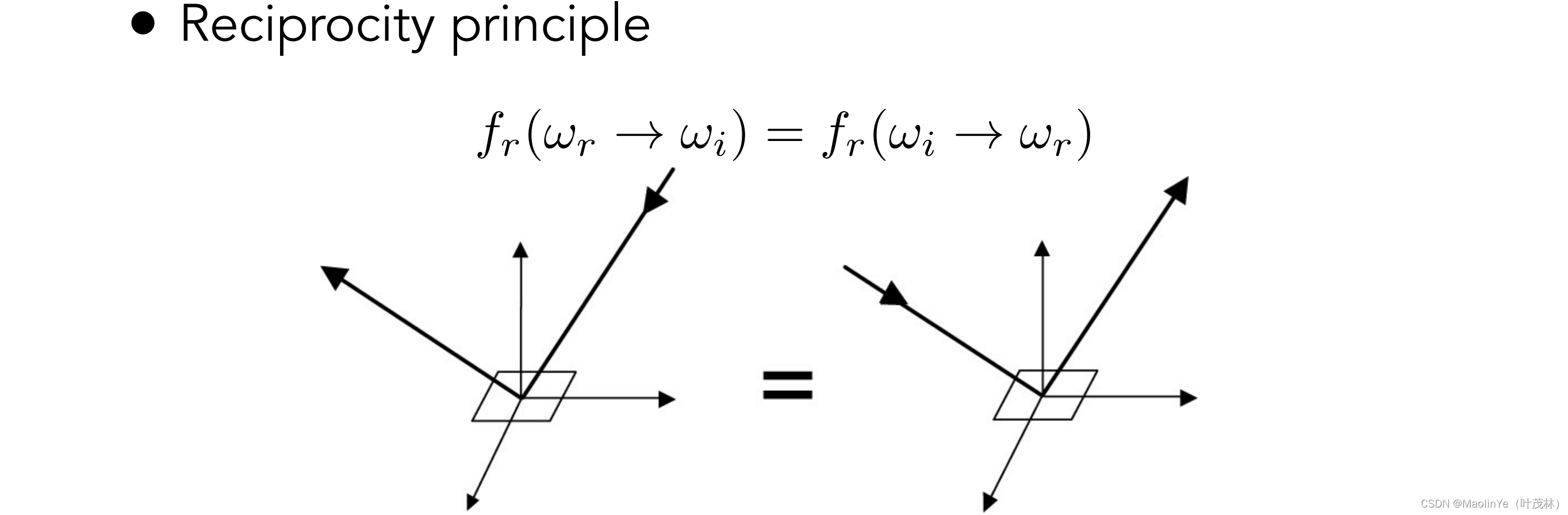
能量守恒
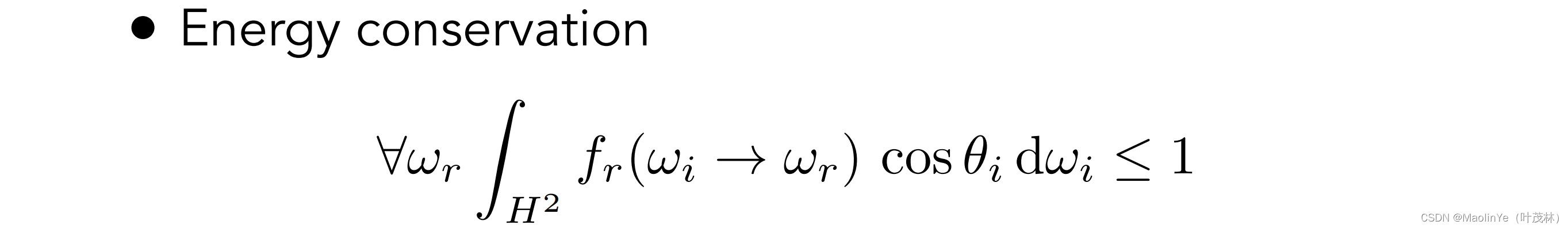
各向同性的BRDF只和相对的水平角有关系
测量BRDF
BRDF描述的是入射方向和出射方向的关系,那怎么去测量它呢,对于一个特定的物体,先用一个光源去照射它,然后记录每个方向的反射,再改变光源照射的方向,继续记录每个方向的反射
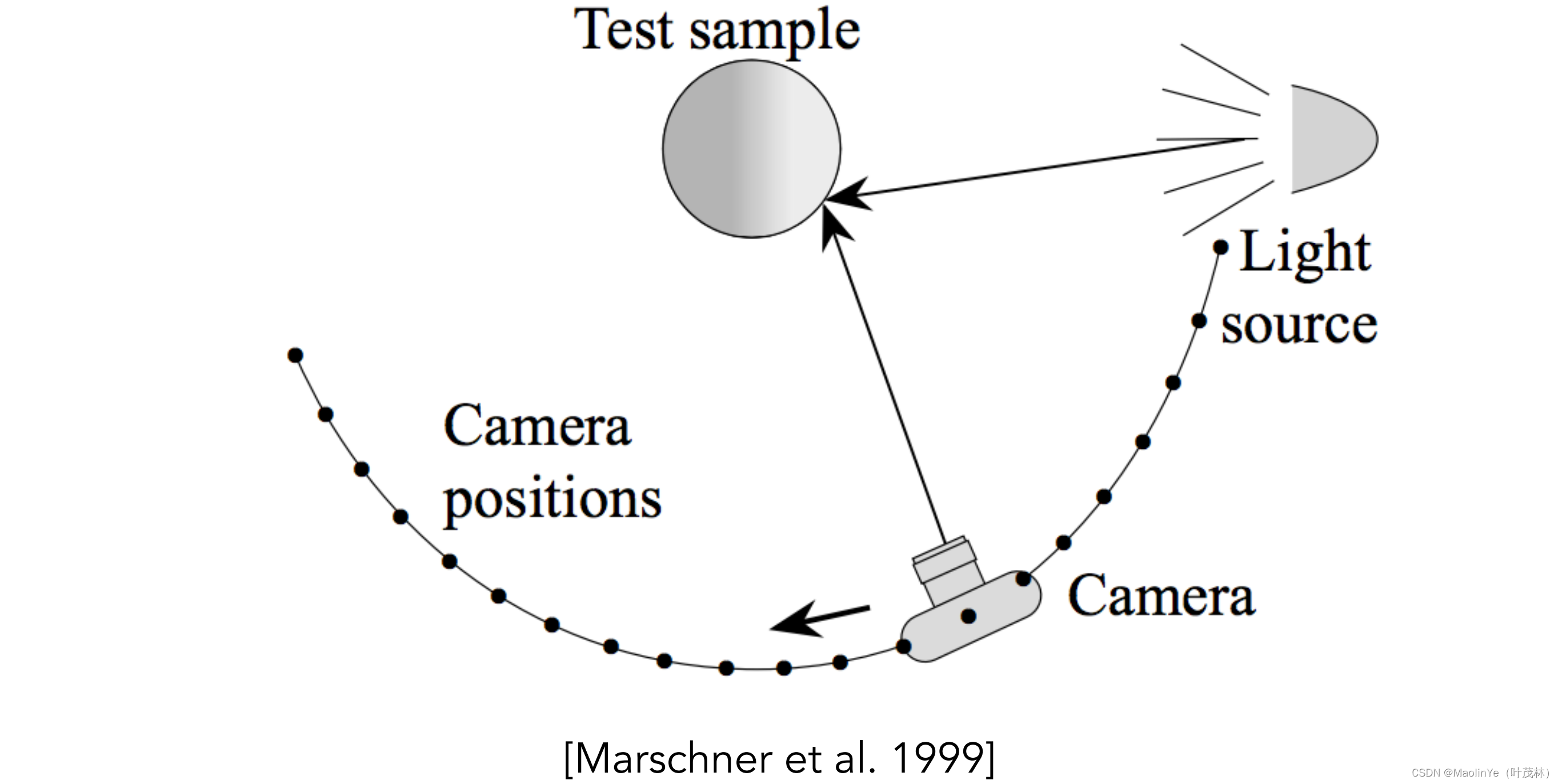
这里是不是有两层循环,但是实际上每个方向是空间角,是用二维向量(,
)表示的,所以实际上是四层循环,如果是各项同性的,因为入射的
和出射的
的差值是固定的,所以可以降到三层循环,如果再考虑BRDF的可逆性,就可以减少一半测量

![CVE-2024-0352:Likeshop任意文件上传漏洞复现 [附POC]](http://pic.xiahunao.cn/CVE-2024-0352:Likeshop任意文件上传漏洞复现 [附POC])

---01实际使用API函数)
)


)

)








)
