文章目录
- 1.统计学习理论
1.统计学习理论
统计学习理论,一款适合零成本搞深度学习的大冤种的方向
从人类学习到机器学习的对比(学习的过程分为归纳和演绎 ),引出泛化和过拟合的概念。
如何表示归纳的函数规律呢?以监督问题为例,需要学习X到Y的映射,先做假设空间,为了使假设空间和真实映射接近,需要损失函数来优化假设空间。学习的目的是学习数据的分布而不是每一个数据点本身,所以希望期望风险最小(期望风险即假设在数据整个分布上的误差的期望),然而需要学习的分布是未知的,所以不能计算期望风险。但是假设在训练集上的误差是可以计算的(即经验风险,损失函数在训练集上的均值),所以下面的目标是追求经验风险最小化。

那么这个假设和假设空间里真正最优得到那个假设所达到的期望风险有多大差距呢?它和全函数类(包含所有可能得映射的函数类里所存在的能达到的最优的假设的风险,即Bayes error差多少),我们可以将经验风险和Bayes error的差距改写成经验风险和假设空间中的所能达到最优的risk的差距(即estimation error,假设空间中最优的risk和Bayes error之间的差距是approximation error),approximation error和具体的训练数据无关,只和假设空间的选择有关(假设空间固定,approximation error就是一个固定值,与训练数据和算法无关),所以只能找estimation error的上界。这里存在trade-off,如果选择更大的假设空间,那么approximation error就会相应地变小。如果假设空间大到包含了最优的Bayes classifier,那么approximation error就是0。但是随着假设空间的增大,训练的cost也会相应增加(亦有可能出现过拟合,estimation error变大,没有泛化能力,没有学到数据背后的规律)

学习数据背后的规律这件事靠谱吗?如何保证学到的数据验证集上靠谱呢?根据大数定律:在随机事件的大量重复中往往会呈现几乎必然的规律,当样本集无限大,样本均值趋近于总体均值。

摆脱对极限和无穷的依赖,人为设定一个界\epsilon,若经验风险和期望风险的差距小于\epsilon则可以接受。霍夫丁不等式帮助判断一个假设的优劣,优劣通过置信度\delta表现,对于一个假设\delta越小越好,\delta越小代表无法接受的结果出现的概率也就越小。霍夫丁不等式就像绑住期望风险和经验风险之间的弹力绳,在具体情况中期望风险和经验风险谁高谁低不好说,但是有了中间的弹力绳,我们用力拉低经验风险,期望风险大概率也可以被拉低,大部分情况下期望风险和经验风险的差距是小于\epsilon的,但是中间是弹力绳,运气不好时,差距可能大于\epsilon,运气不好时超过\epsilon多少也是未知的,这样的双重不确定性听起来不靠谱

构建靠谱的框架,期望风险和经验风险都和假设h有关(假设h取值不同,期望风险和经验风险都不同)。下面图像,蓝色曲线是期望风险,黑色曲线是经验风险,都是以h为变量的函数,蓝色曲线最低点期望误差最小是optimal solution h^*,黑色曲线最低点是经验风险最小化的solution,不光假设影响经验风险,训练集也影响。但是不同的训练集对期望风险不会有影响,因为期望风险本身就是在全样本集上误差的期望。
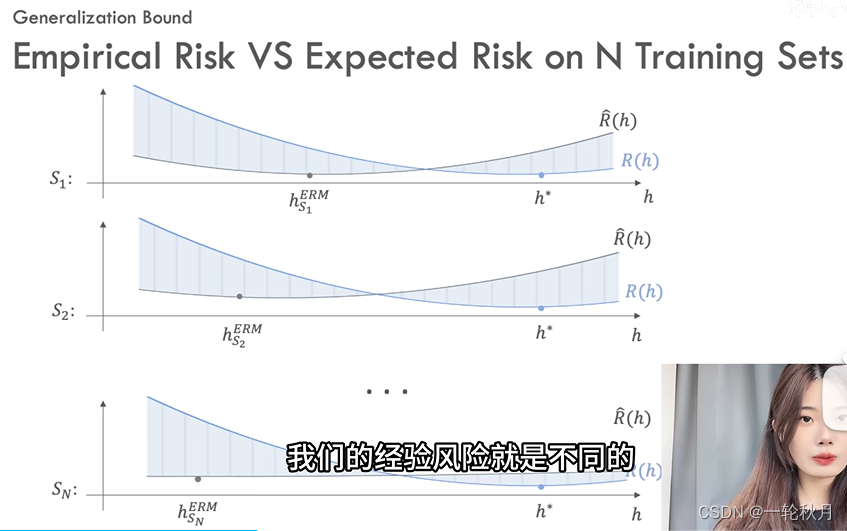
希望找到的假设期望风险也能越小越好,期望风险和经验风险的差值超过\epsilon为红色,小于为灰色,同样的假设在数据集1上小于\epsilon,但是在数据集2上又大于\epsilon
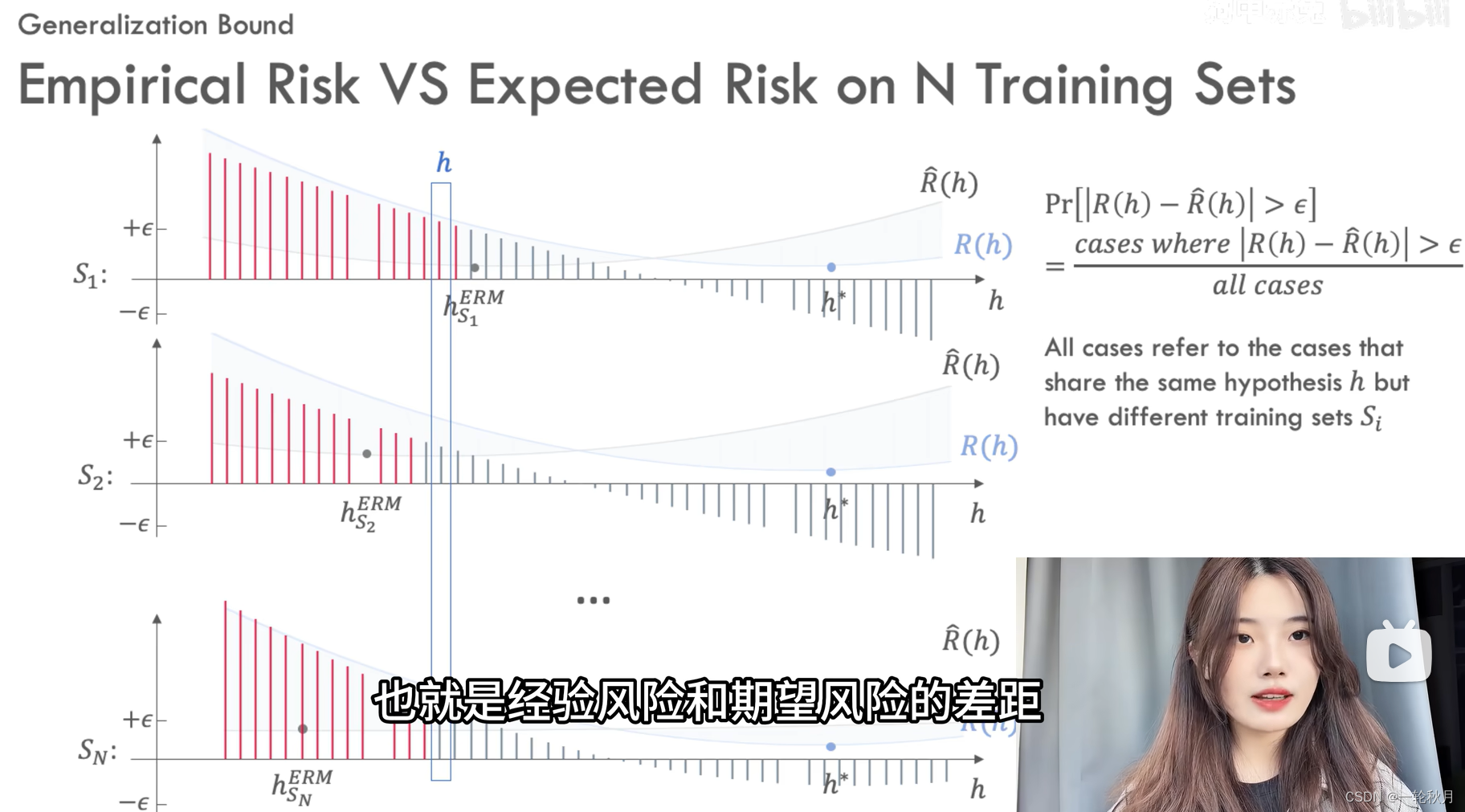
对于一个假设h,期望风险减去假设风险的绝对值大于\epsilon的概率,即在所有数据集上红色格子数量除以格子的总数,我们希望它可以小于一个上界\delta

定义PAC学习框架,提供了一套严格的形式化语言,来陈述和刻画可学习性
和样本复杂度的问题。我们希望在假设空间空间中找到期望风险为0的假设,但基本上不可能。所以退而求其次,只要期望风险小于等于\epsilon,则是可接受的,近似正确的(approximately correct)。我们也不是100%要求这个假设近似正确,它不需要对所有任意的数据都能成功预测,只要预测失败的概率小于非常小的数字\delta,我们就认为是可能正确的,也就是probably correct,我们把成功概率的下界1-\delta叫做置信度。满足上面两个条件,则我们的学习算法能够从假设空间h中辨识概念类c(即模型能够在合理的训练数据量中,通过合理的计算量,学到了一个很好的近似解)。不难发现,所需要的样本量和\epsilon \delta 算法复杂度 目标概念的复杂度都有关。算法也要考虑复杂度,如果算法运行复杂度也在这个多项式内,那么称概念类c是PAC可学习的。如果算法A是存在的,那么称此算法为这个概念类的一个PAC学习算法。如果算法处理每个样本的时间都是常数,那么算法的复杂度等价于样本的复杂度,如果时间复杂度过大,即使理论上行得通,我们也是跑不出一个结果的。

目标概念有两种可能得情况,1.我们想找的目标概念c在我们的假设空间;2.不在假设空间。目标概念c属于假设集h称为一致情况,反之称为不一致情况。考虑第一种情况:目标概念c在我们的假设空间,则排除所有在训练集s上除了错的假设了,但是假设空间里可能存在不止一个在训练集上不犯错的假设,这样我们没法通过训练集来判断这些假设哪个是最优的。那么我们先假设,假设h虽然在训练集上没有犯错,但是他的期望风险大于\epsilon。那么对于从分布D上采样得到的任意一个样本,我们的假设没犯错的概率小于1-\epsilon。那么h和包含m个服从D的训练集s一致的概率是小于(1-\epsilon)^m的。因为我们没有办法区分等效的假设,所以我们也不知道我们的学习算法选择了哪个假设,所以我们需要一个uniform convergence bound,也就是对所有一致的假设都成立的bound。根据联合界定理,事件和的概率小于等于事件概率的和,条件概率的定义是已知事件A发生的情况下,事件B发生的概率等于AB同时发生的概率和事件A发生的概率的比,事件A发生的概率一定小于等于1。所以A发生的情况下,事件B发生的条件概率大于等于AB同时发生的概率。回忆刚才推过的假设在训练集s上不犯错,但是期望风险大于\epsilon的概率是小于(1-\epsilon)^m的。我们需要所有的泛化误差大于\epsilon的一致假设出现的概率之和不大于\delta,这样我们容易得到样本复杂度

不难看出当假设空间有限,算法A是一个PAC学习算法,样本复杂度是一个关于1/\epsilon和1/\delta的多项式。同时期望风险的上界是随着样本规模m的增长而下降的,泛化误差减小的速率是O(1/m),我们平时也会发现使用大规模的有标签的数据集会让训练效果更好,同时期望风险的上界也随着假设集的势的增长而增长(即我们的假设集越大我们越难学到我们想要的东西,只不过他的增长速率是log级别的)

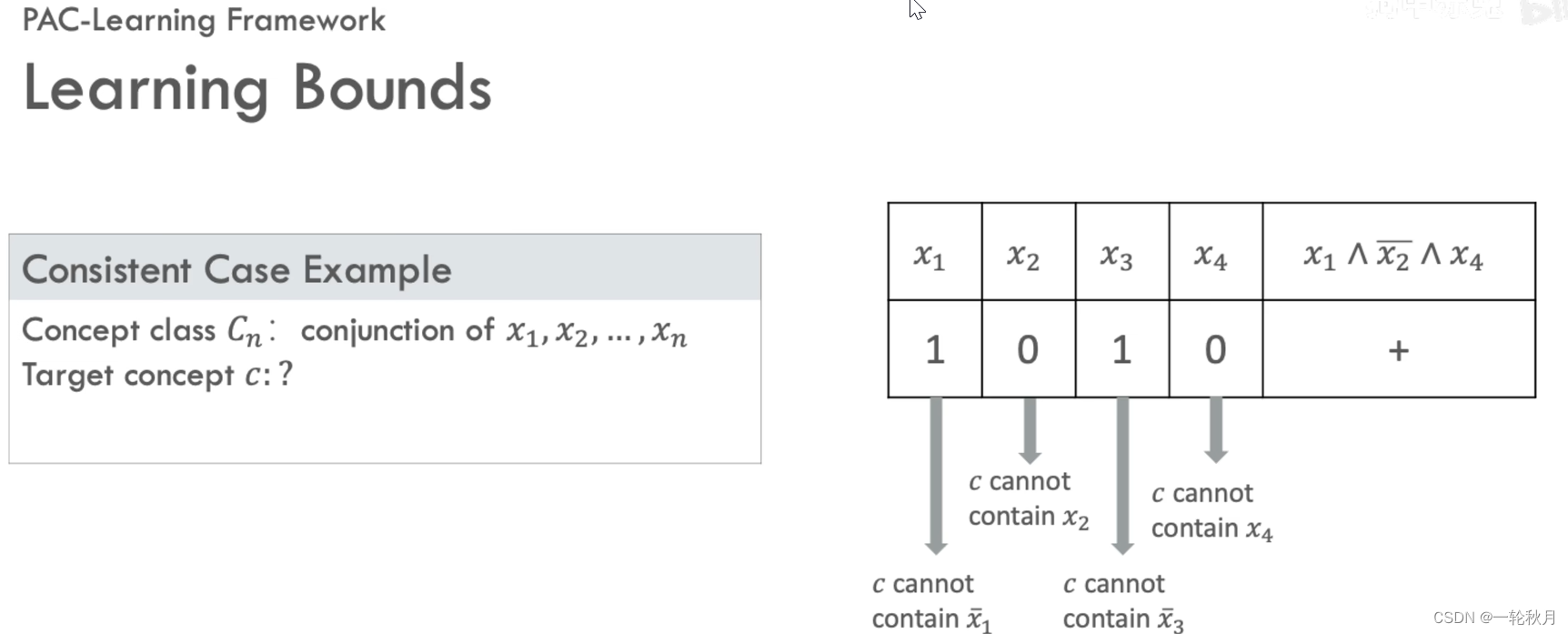
证明一致情形的例子,考虑概念类C_n是最多n个boolean变量的合取x_1,x_2 x_n,当n=4,想学习的概念类是x_1与非x_2与x_4,1001是正样本,1000是负样本。我们不知道目标概念,只知道n=4,1001是个正样本,我们通过分析样本得到一些信息:既然1001是正样本,则说明目标概念不包括非x_1和非x_3,也不包括x_2和x_4,但是负样本就不能传递这么多的信息,因为我们不知道x_1 x_2 x_3 x_4哪个是错的

n=6的情况,我们想找到一个算法,来根据正样本找到一个一致的假设,那么对于每一个正样本,如果它的哪一位是1,那么目标概念就应该排除它的否定式,如果它的哪一位是0,我们就可以排除它本身,按此方法推出目标概念是非x_1 与x_2 与x_5与 x_6。这个问题我们是知道假设空间的大小的
![CVE-2024-0352:Likeshop任意文件上传漏洞复现 [附POC]](http://pic.xiahunao.cn/CVE-2024-0352:Likeshop任意文件上传漏洞复现 [附POC])

---01实际使用API函数)
)


)

)








)

