LeetCode、790. 多米诺和托米诺平铺【中等，二维DP，可转一维】

文章目录

前言
LeetCode、790. 多米诺和托米诺平铺【中等，二维DP，可转一维】
- 题目与分类
- 思路
- - 二维解法
  - 二维转一维
资料获取

前言

博主介绍：✌目前全网粉丝2W+，csdn博客专家、Java领域优质创作者，博客之星、阿里云平台优质作者、专注于Java后端技术领域。

涵盖技术内容：Java后端、算法、分布式微服务、中间件、前端、运维、ROS等。

博主所有博客文件目录索引：博客目录索引(持续更新)

视频平台：b站-Coder长路

LeetCode、790. 多米诺和托米诺平铺【中等，二维DP，可转一维】

题目与分类

题目链接：LeetCode、790. 多米诺和托米诺平铺

分类：动态规划/线性DP

思路

思路描述：以第i列来作为递推形式，初始第一列(二行一列)是固定满的，目的就是初始化，之后每一列（可以说每一组）都是基于上一列的四个状态来与当前可组合的多米诺和托米诺来构成新的一种组合。

下面是多米诺和托米诺的各种状态：

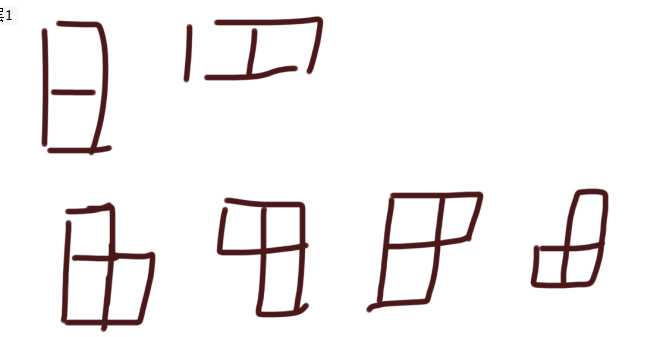
下面图示i位置的多个图案右边的序号下每一个正方形其中的第一列就指的是上一层四个状态中的其中一个状态，根据当前应该成为的状态来看是否可以添加一个多米诺和托米诺来组成当前所属的状态，经过n轮这样子推导，最终即可推导得到所有满平铺的方案数量。

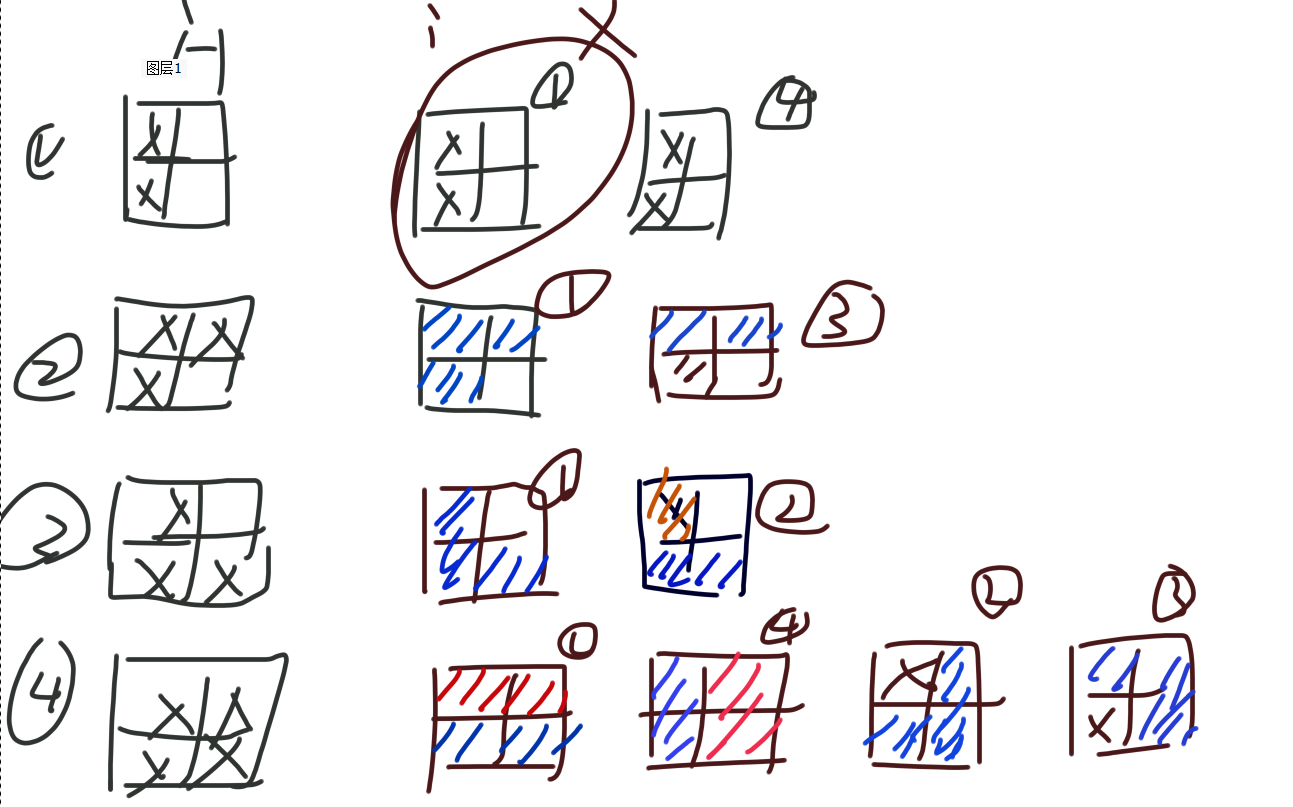
二维解法

复杂度分析：时间复杂度O(n)；空间复杂度O(n)

class Solution {public static final int MOD = 1000000007;//按照【列】来进行递推方程 提前设置好每一列的状态情况//n最大1000//dp[0][0-2] = 0  dp[0][3] = 1//递推：n列  i为列//   dp[i][0] = dp[i - 1][3]//   dp[i][1] = dp[i - 1][0] + dp[i - 1][2]//   dp[i][2] = dp[i - 1][0] + dp[i - 1][1]//   dp[i][3] = dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][2] + dp[i - 1][3]public int numTilings(int n) {int[][] dp  = new int[n + 1][4];//初始化dp[0][3] = 1;//递推for (int i = 1; i <= n; i ++) {dp[i][0] = dp[i - 1][3] % MOD;dp[i][1] = MODD(dp[i - 1][0], dp[i - 1][2]);dp[i][2] = MODD(dp[i - 1][0], dp[i - 1][1]);dp[i][3] = MODD(MODD(dp[i - 1][0], dp[i - 1][1]), MODD(dp[i - 1][2], dp[i - 1][3]));}return dp[n][3];}// 对两个int进行取%public int MODD(int a, int b) {return (a + b) % MOD;}
}

二维转一维

说明：可以看到当前题解是基于二维DP来推导的，在二维中我们可以看到当前层每次计算新的数量值时之后使用到上一层，那么就i很容易的二维转一维。

复杂度分析：时间复杂度O(n)；空间复杂度O(1)

class Solution {public static final int MOD = 1000000007;//二维转一维public int numTilings(int n) {int t1 = 0, t2 = 0, t3 = 0, t4 = 1;//递推for (int i = 1; i <= n; i ++) {int tmp1 = t1, tmp2 = t2, tmp3 = t3, tmp4 = t4;t1 = tmp4 % MOD;t2 = MODD(tmp1, tmp3);t3 = MODD(tmp1, tmp2);t4 = MODD(MODD(tmp1, tmp2), MODD(tmp3, tmp4));}return t4;}// 对两个int进行取%public int MODD(int a, int b) {return (a + b) % MOD;}
}