第一次参加这种比赛,虽然是c类赛事,但是是ccf主办的,难度还是有点的,主要是前面签到题主要是思想,后面的题目难度太高,身为力扣只刷了一百多道题目的我解决不了,这几道我只做了B,C题,E题超时了,这些题目的时间限制实在是太高了,这次只能是来学习学习了。顺便附上一下自己的代码,有点丑勿喷,希望有大神能出个题解,感谢
A题:
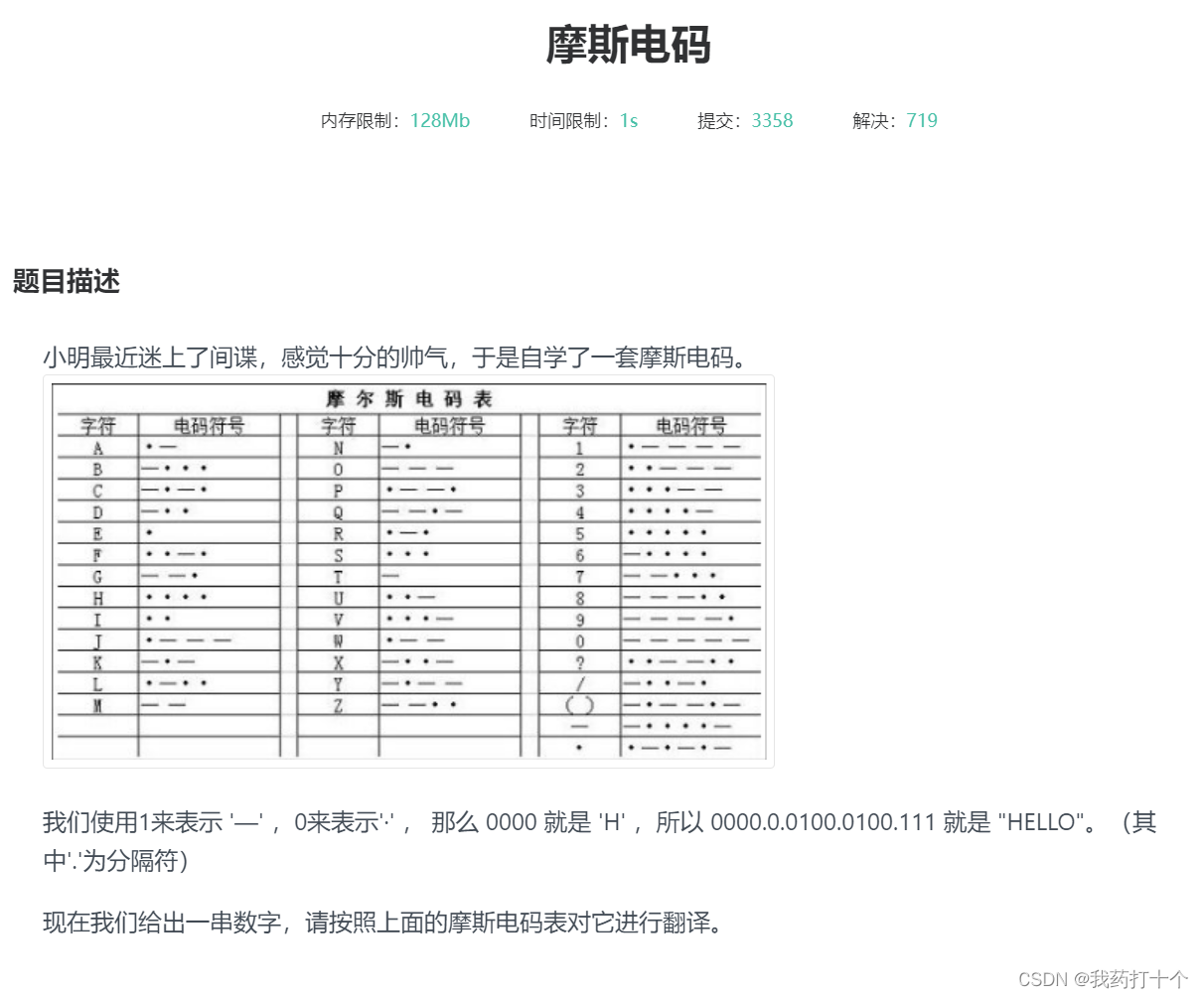
B题:
if __name__ in '__main__':Input = input()n,m = int(Input.split(' ')[0]),int(Input.split(' ')[1])MIN = min(n,m)MAX = max(n,m)first_x = MINfirst_y = MINif n == m:k = 1else:k = 2 if n<m else 3for i in range(2):if k == 0:distance = min(n-first_x,m-first_y)first_x += distancefirst_y += distanceelif k == 1:distance = min(first_x,first_y)first_x -= distancefirst_y -= distanceelif k == 2:distance = min(first_x,m-first_y)first_x -= distancefirst_y += distanceelif k == 3:distance = min(n-first_x,first_y)first_x += distancefirst_y -= distanceflag = 0if first_x == 0 and first_y == 0:k = 0flag = 1elif first_x == 0 and first_y == m:k = 3flag = 1elif first_x == n and first_y == 0:k = 2flag = 1elif first_x == n and first_y == m:k = 1flag = 1if flag == 0:if k == 0:if first_y == m:k = 3elif first_x == n:k = 2elif k == 1:if first_x == 0:k = 3elif first_y == 0:k = 2elif k == 2:if first_x == 0:k = 0elif first_y == m:k = 1elif k == 3:if first_y == 0:k = 0elif first_x == n:k = 1print(first_x,first_y)C题:
if __name__ in '__main__':Input = input()n,m = int(Input.split(' ')[0]),int(Input.split(' ')[1])n += 1top = 1while((n ** top) <= m):top += 1top -= 1temp = topnums = []while(top > 0):num = m // (n**top)m -= num * (n**top)nums.append(num)top -= 1if m > 0:nums.append(m)res = ''for i, snum in enumerate(nums):if snum == 0:temp -= 1continueif temp > 1 and snum > 1:res += str(snum) + 'x^' + str(temp) + '+'elif temp > 1 and snum == 1:res += 'x^' + str(temp) + '+'elif temp == 1 and snum > 1:res += str(snum) + 'x+'elif temp == 1 and snum == 1:res += 'x+'else:res += str(snum)temp -= 1print(res)D题:
E题:
import math
def check(num):if num == 2 or num == 3:return Trueend = num ** (1/2)for i in range(2,int(end)+1):if num % i == 0:return Falseif num == 1:return Falsereturn True
if __name__ in '__main__':n = int(input())res = 0for i in range(2,n):if check(i):if check(n-i) == False:if n-i != 1:res += 2else:res += 1end = n-istart = 2while(start < end):if (n-i) % start == 0:res += 2end /= startstart += 1print(res)F题:
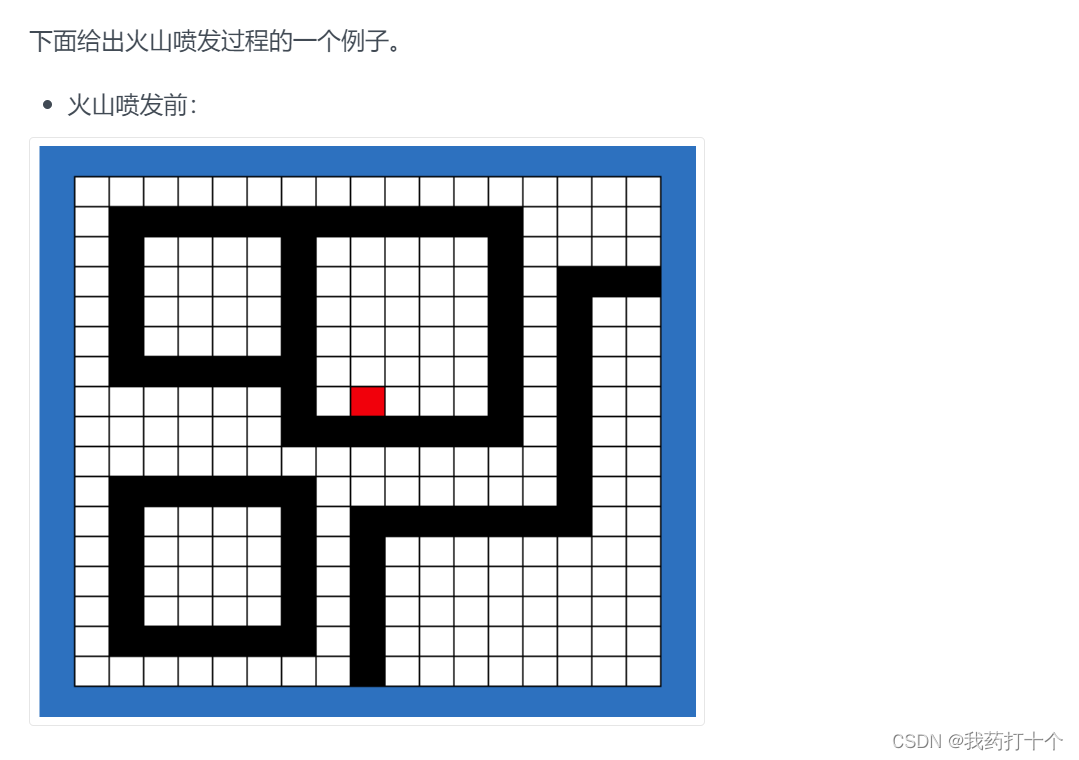
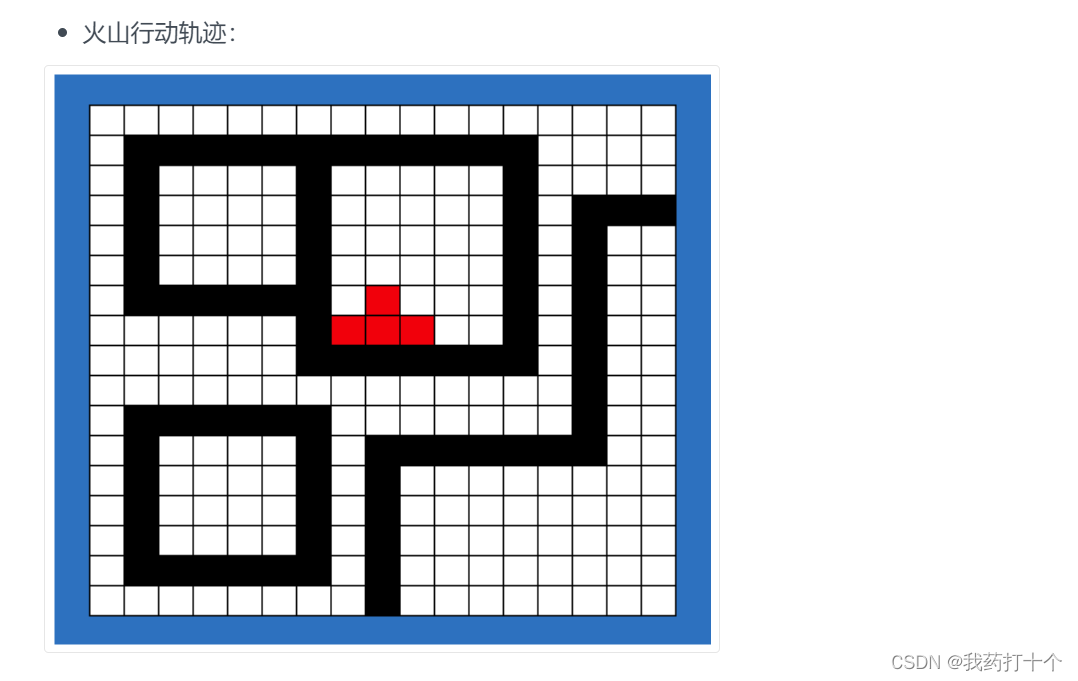
G题:
H题:
I题:
希望这篇博客对你有帮助,希望有大神出一下题解!!!!







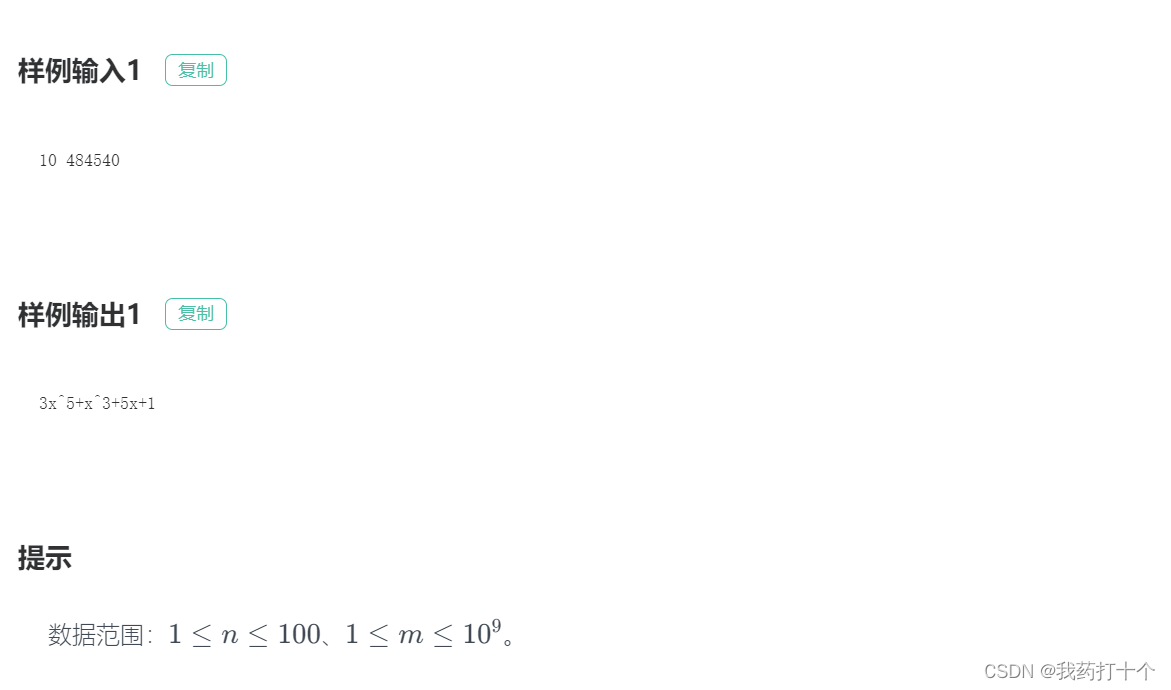



















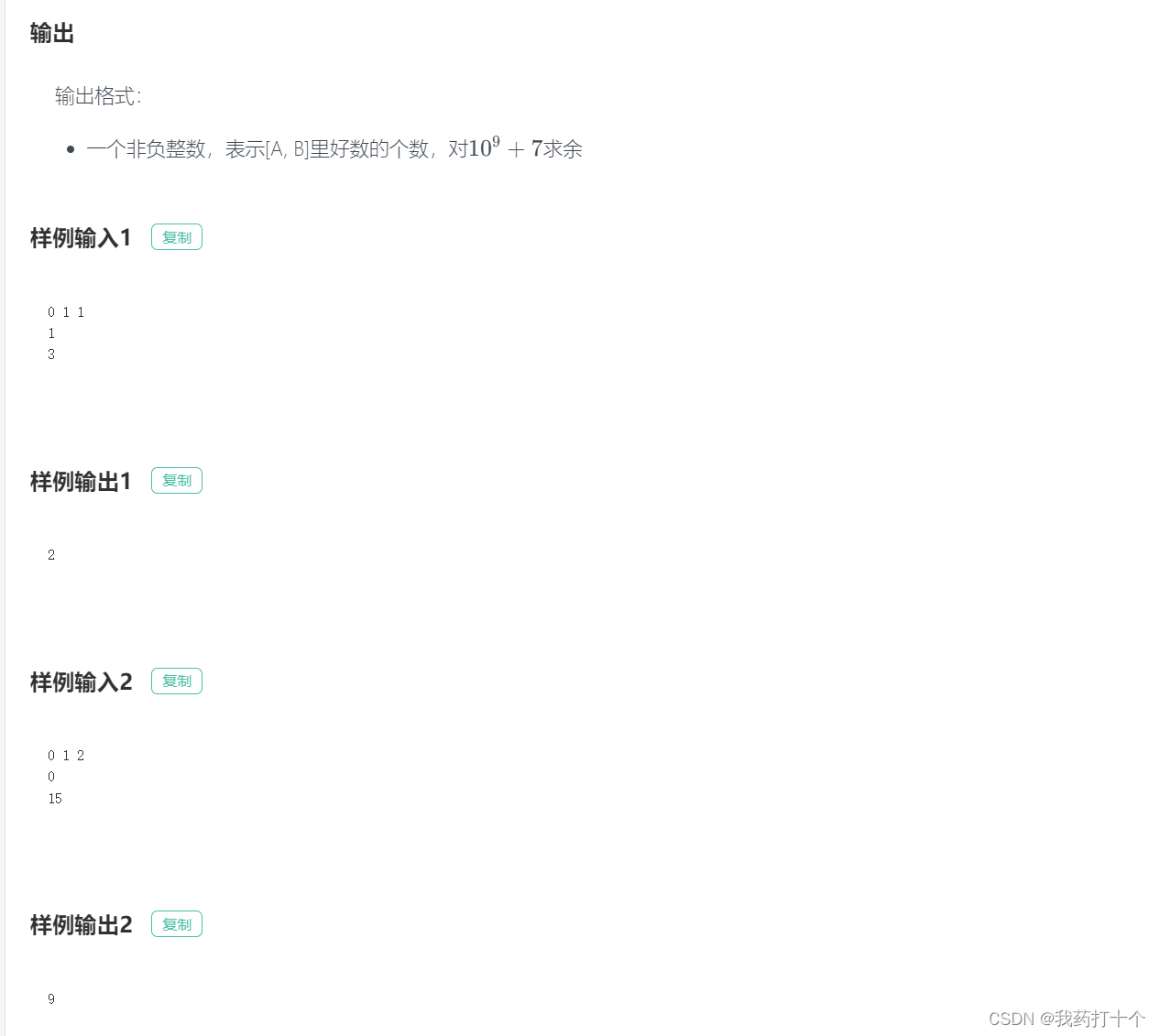





-- 缓存cache用法总结)

——第115天:基于selenium实现反反爬策略之隐藏浏览器指纹特征)




)



)


)
)
