目录
- 里程计模型
- 两轮差分底盘的运动学模型
- 优点
- 差分模型
- 三轮全向底盘的运动学模型
- 优点
- 全向模型
- 航迹推算(Dead Reckoning)
- 里程计标定
- 线性最小二乘的基本原理
- 最小二乘的直线拟合
- 最小二乘在里程计标定中的应用
- 方法
里程计模型
里程计相关介绍
两轮差分底盘的运动学模型
优点
- 结构简单,越障性能好
- 便宜,应该是所有底盘构型中最便宜的类型,只需要两个电机
- 模型简单
差分模型
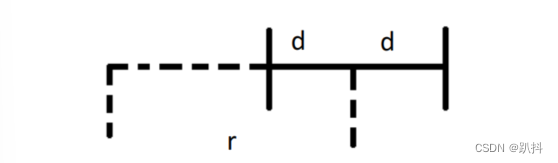
差分运动底盘实际上是一个欠驱动系统。自由度为3(即X,Y,θ),但是驱动数只有2个(即VL,VR,左轮速度和右轮速度)。欠驱动系统造成差分模型的平移运动和旋转运动是耦合的,无法单独分解运动。
差分底盘只能做一种运动——圆弧运动。对于直线运动而言,r趋于∞;对于纯旋转而言,r趋于0,实际上还是两个圆弧运动。其运动学模型如下:
- v,ω为底盘中心线速度和角速度
- v_L,v_R为左右两轮的速度
- d为轮子距离底盘中心的距离
推导过程:
三轮全向底盘的运动学模型
优点
- 任何方向平移
- 结构简单
- 全驱动系统,可以完全解耦
- 可以进行运动学分解
全向模型
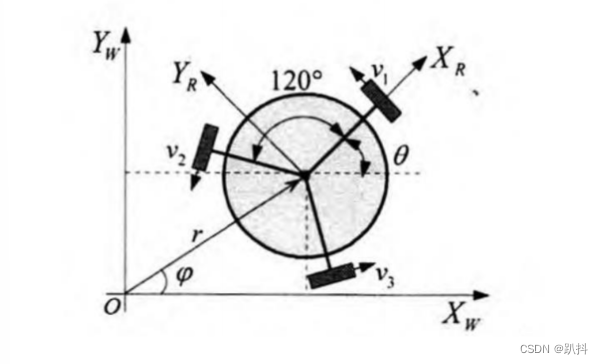
运动分解——平移X:
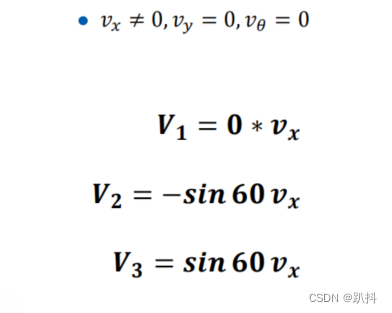
运动分解——平移Y:
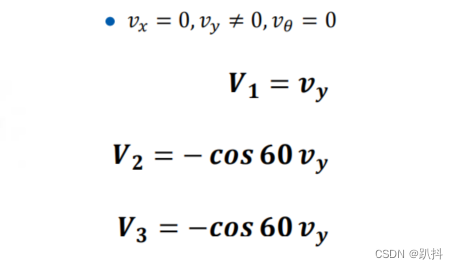
运动分解——旋转:
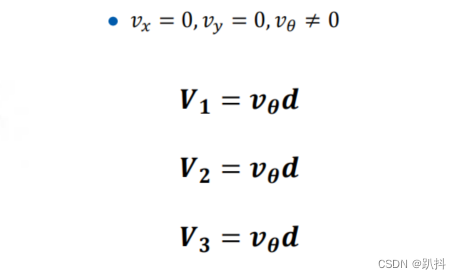
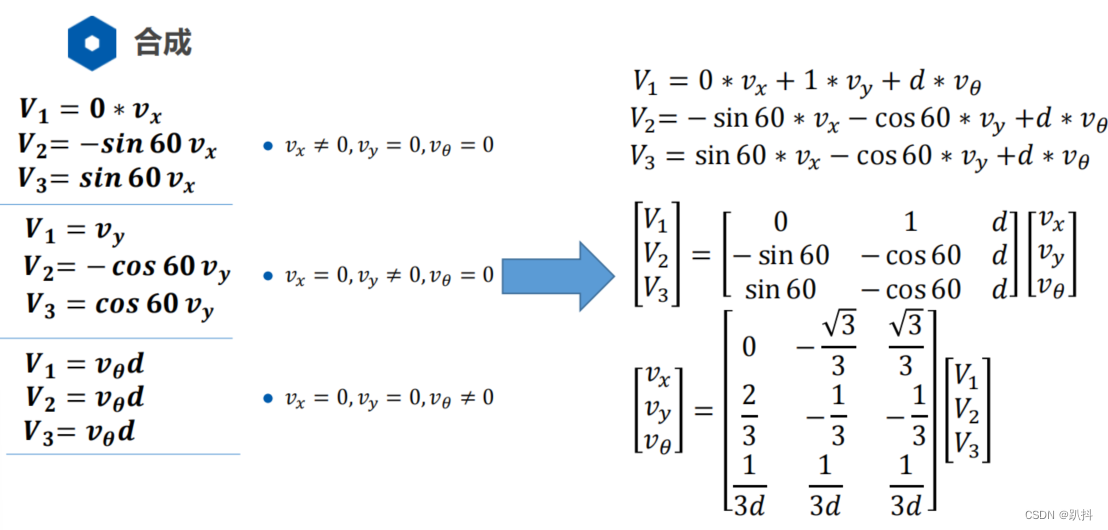
合成:
航迹推算(Dead Reckoning)
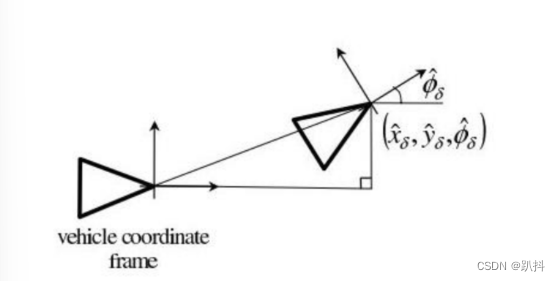
递推公式:

里程计标定
里程计标定的目的是减小里程计的误差,提高机器人导航的精度和可靠性。 通过标定,可以确定里程计的误差模型和参数,从而对机器人的位移和姿态进行更准确的计算。
线性最小二乘的基本原理
Ax=b的每一行代表一个约束,列代表未知数的维数。由于几乎不可能把所有方程同时满足,所以绝大多数情况为超定方程组。


最小二乘的直线拟合
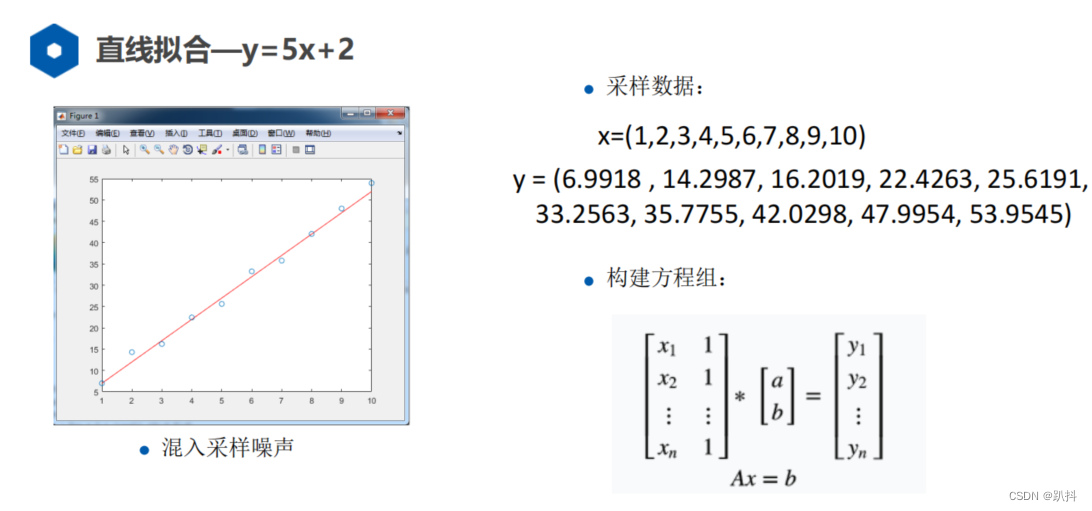
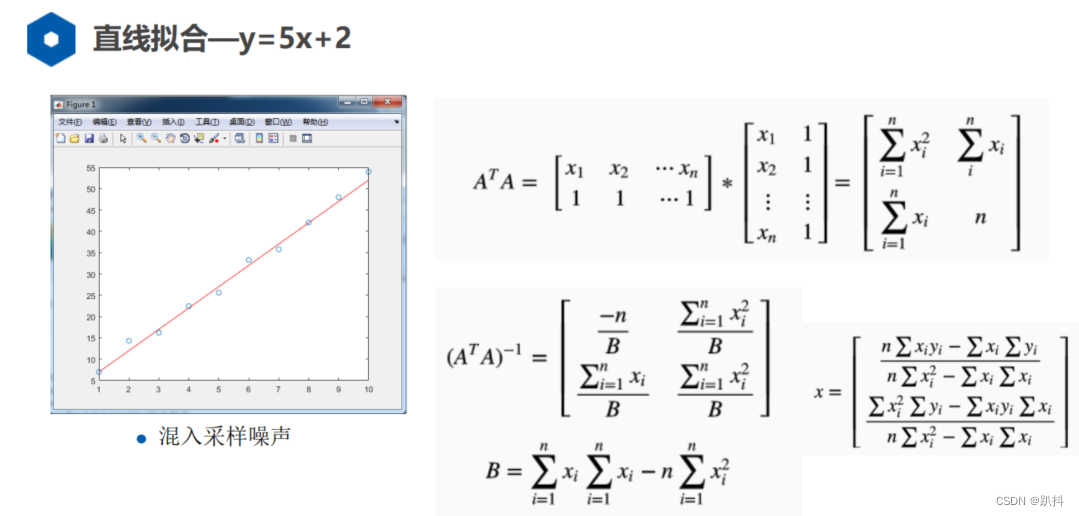
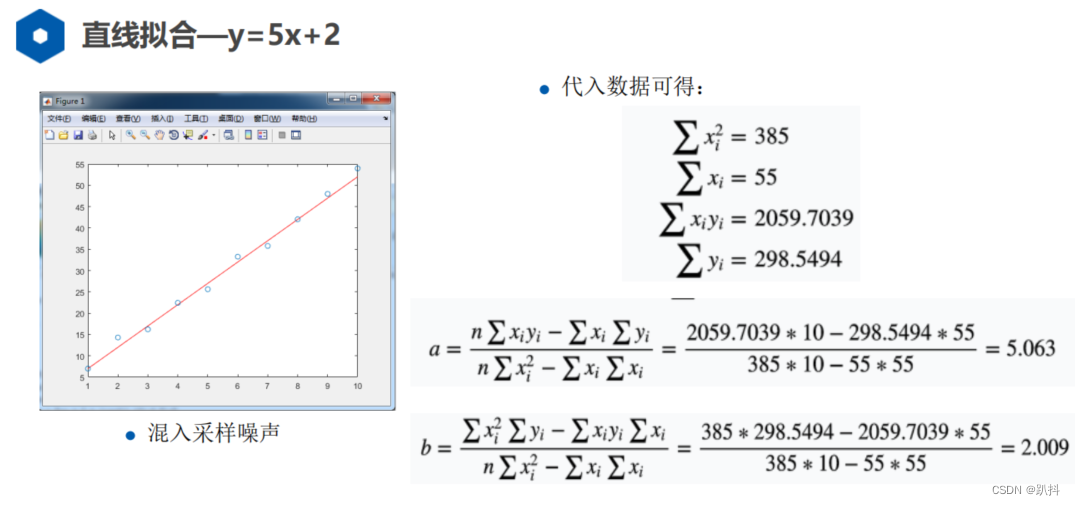
最小二乘在里程计标定中的应用
方法
- 直接线性方法:通用性强、实现简单、精度不高
- 基于模型的方法:精度高、实现复杂、特异性高

u_i*表示激光雷达测得的第i帧与第j帧的相对位置关系,即u_i*=p_i-1 p_j。同理,u_i则为由里程计测量得到的同一关系。
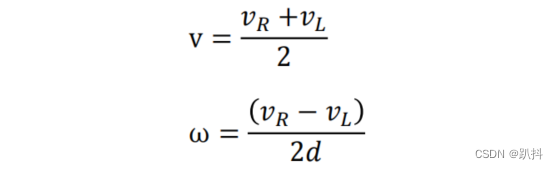
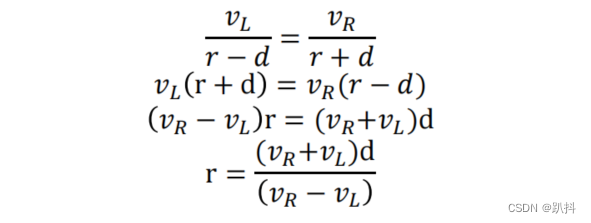
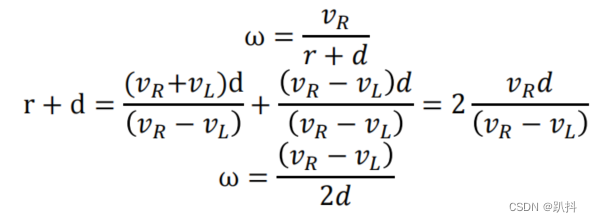
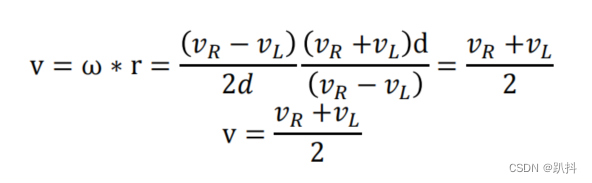







)
-Java版)



)
)





