彻底学会系列：一、机器学习之线性回归（一）

1.基本概念(basic concept)

线性回归： 有监督学习的一种算法。主要关注多个因变量和一个目标变量之间的关系。
因变量： 影响目标变量的因素： $X_1, X_2...$ ，连续值或离散值。
目标变量： 需要预测的值: $t a r g e t$ ， $y$
因变量和目标变量之间的关系: 即模型，model

1.1连续值(continuous value)

连续值是可以在一个区间范围内取任意值的变量。例如，身高、体重、温度、时间等都是连续值
在这里插入图片描述

1.2离散值(discrete value)

离散值是只能取有限个数值或者可数值的变量。例如，学生人数、家庭成员数、考试分数等都是离散值
在这里插入图片描述

1.3简单线性回归(simple linear regression)

简单线性回归对应的公式： $y = w x + b$
$y$ 是目标变量即未来要预测的值
$x$ 是影响 $y$ 的因素
$w, b$ 是公式上的参数即要求的模型， $w$ 就是斜率， $b$ 就是截距
一元一次方程：
在这里插入图片描述
一元二次方程：

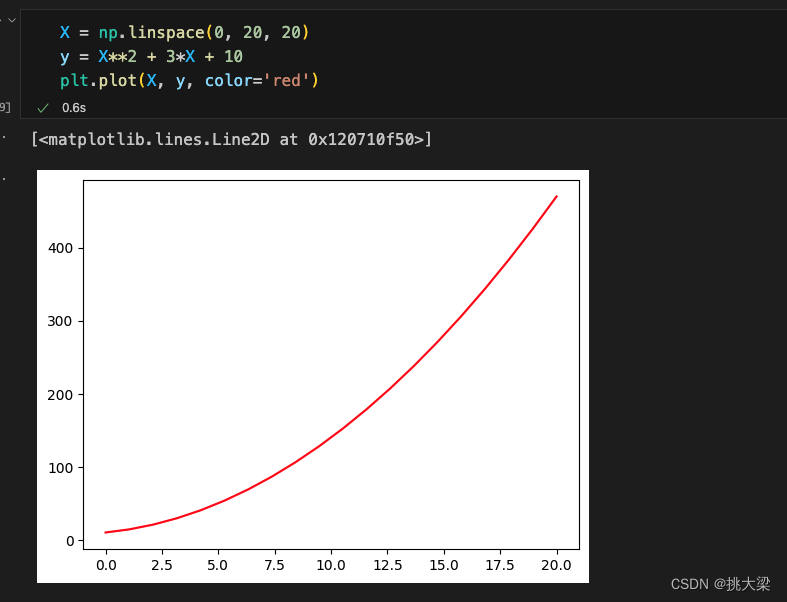
1.4多元线性回归(multiple linear regression)

现实生活中，往往影响结果 y 的因素不止一个，有可能是 n 个， $X_1,X_2,X_n...$
多元线性回归公式：

$\hat y = w_1X_1 + w_2X_2 ... w_nX_n + b$

b是截距，也可以表示成：

$\hat y = w_1X_1 + w_2X_2 ... w_nX_n + w_0$

使用向量来表示：

$\hat y = W^TX$

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression# 转化矩阵
x1 = np.random.randint(-150, 150, size=(300, 1))
x2 = np.random.randint(0, 300, size=(300, 1))# 斜率和截距，随机生成
w = np.random.randint(1, 5, size=2)
b = np.random.randint(1, 10, size=1)# 根据二元一次方程计算目标值y,并加上"噪声"
y = x1 * w[0] + x2 * w[1] + b + np.random.randn(300, 1)
fig = plt.figure(figsize=(9, 6))
ax = plt.subplot(111, projection='3d')
ax.scatter(x1, x2, y)  # 三维散点图
ax.view_init(elev=10, azim=-20)  # 调整视角
#
X = np.concatenate([x1, x2], axis=1)
model = LinearRegression()
model.fit(X, y)
w_ = model.coef_.reshape(-1)
b_ = model.intercept_print('一元一次方程真实的斜率和截距是：\n', w, b)
print('通过scikit-learn求解的斜率和截距是：\n', w_, b_)x = np.linspace(-150, 150, 100)
y = np.linspace(0, 300, 100)
z = x * w_[0] + y * w_[1] + b_
ax.plot(x, y, z, color='green')plt.show()

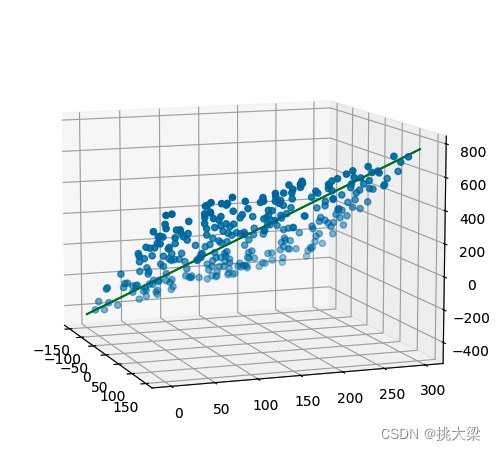
在这里插入图片描述

1.5 最优解(optimal solution)

$y$ : 真实值(actual value)
$\hat y$ : 预测值(predicted value), 根据因变量 $X_1,X_2...$ 和计算出来的参数w,b得到
$error$ : 误差，预测值和真实值的差距（ $\varepsilon$ ）
最优解: 尽可能的找到一个模型使得整体的误差最小，通常叫做损失 Loss，通过损失函数Loss Function计算得到。

from sklearn.linear_model import LinearRegressionX = np.linspace(0, 10, num=30).reshape(-1, 1)
w = np.random.randint(1, 5, size=1)
b = np.random.randint(1, 10, size=1)y = X * w + b + np.random.randn(30, 1)
plt.scatter(X, y)model = LinearRegression()
model.fit(X, y)
w_ = model.coef_
b_ = model.intercept_print('一元一次方程真实的斜率和截距是：\n', w, b)
print('通过scikit-learn求解的斜率和截距是：\n', w_, b_)plt.plot(X, X.dot(w_) + b_, color='green')
plt.show()

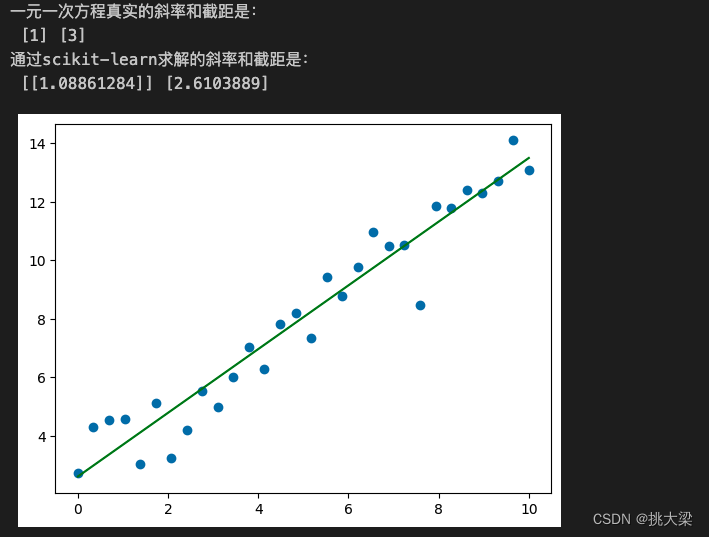
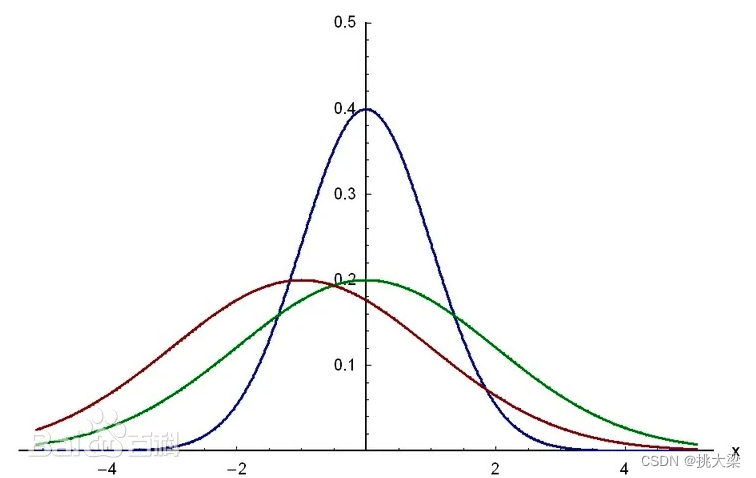
在这里插入图片描述

1.6 高斯密度函数 (Gaussian Density Function):

高斯密度函数（Gaussian Density Function）也被称为正态分布或钟形曲线，是统计学中最常用的概率分布之一。其概率密度函数（Probability Density Function, PDF）的表达式如下：

$\ f(x; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$

其中，(x) 是变量， $\mu$ 是均值， $\sigma^2$ 是方差。

$\mu$ 表示分布的均值，决定了曲线的中心位置。
$\sigma^2$ 是方差，决定了曲线的宽度或分布的离散程度。标准差 $\sigma$ 是方差的平方根。

高斯密度函数的特征包括：

钟形曲线形状： 高斯分布呈现出典型的钟形曲线，对称分布在均值周围。
68-95-99.7 规则： 大约68% 的数据在均值的一个标准差范围内，95% 在两个标准差范围内，99.7% 在三个标准差范围内。
均值和方差唯一决定分布： 高斯分布的均值和方差是唯一确定整个分布的两个参数。

1.8 最大似然估计(Maximum Likelihood Estimation)

是一种用于估计模型参数的统计方法。它基于概率论的观点，寻找使观测数据出现的概率最大的参数值。通常记为 $L (θ ∣ d a t a)$ ，其中 θ 是待估计的参数，为了方便计算，通常取似然函数的对数，得到对数似然函数（Log-Likelihood），记为 $\ell(\theta | \text{data})$

公式：
$\text{Likelihood Function: } L(\theta | \text{data}) = \prod_{i=1}^{n} P(X_i; \theta)$
$\text{Log-Likelihood Function: } \ell(\theta | \text{data}) = \sum_{i=1}^{n} \log P(X_i; \theta)$