数据结构与算法：图论（邻接表板子+BFS宽搜、DFS深搜+拓扑排序板子+最小生成树MST的Prim算法、Kruskal算法、Dijkstra算法）

前言

图的难点主要在于图的表达形式非常多，即数据结构实现的形式很多。算法本身不是很难理解。所以建议精通一种数据结构后遇到相关题写个转换数据结构的接口，再套自己的板子。

邻接表板子（图的定义和生成）

public class Graph{public HashMap<Integer,Node>nodes;//点集，第一个参数是点的编号。和Node类中的value一致。不一定是Integer类型的，要看具体的题，有的题点编号为字母。public HashSet<Edge>edges;//边集public Graph(){nodes = new HashMap<>();edges = new HashSet<>();}
}public class Node{public int value;//点的编号，不一定是Integer类型的，要看具体的题，有的题点编号为字母。public int in;//入度public int out;//出度public ArrayList<Node>nexts;//出去的边直接相连的邻居。public ArrayList<Edge>edges//出去的边public Node(int value){this.value=value;in = 0;out = 0;nexts = new ArrayList<>();edges = new ArrayList<>();}
}public class Edge{public int weight;//边上权重public Node from;public Node to;public Edge(int weight,Node from,Node to){this.weight=weight;this.from=from;this.to=to;}
}//现在题目是用三元组来表示图，即给多个三元组{a,b,c},a表示边的起点，b表示边的终点，c表示边的权重。
public static Graph createGraph(Integer[][] matrix){Graph graph = new Graph();for(int i=0;i<matrix.length;i++){Integer from = matrix[0][0];Integer to = matrix[0][1];Integer weight = matrix[0][2];if(!graph.nodes.containsKey(from)){//没有把边的起点加入点集graph.nodes.put(from,new Node(from));}if(!graph.nodes.containsKey(to)){//没有把边的终点加入点集graph.nodes.put(to,new Node(to));}Node fromNode = graph.nodes.get(from);//拿到起点Node toNode = graph.nodes.get(to);//拿到终点Edge newEdge = new Edge(weight,fromNode,toNode);//构造边graph.edges.add(newEdge);fromNode.nexts.add(toNode);fromNode.edges.add(newEdge);fromNode.out++;toNode.in++;}return graph;
}

BFS、DFS板子

图和二叉树的宽搜最大的不同的就是，图是可能有环的。二叉树是没环的，所以图可能死循环卡住，所以需要额外记录是否有访问过，一般是哈希表或者数组。
深搜是点入栈之前就需要处理了，广搜是点入队列之后开始处理。


public static void bfs(Node node){if(node==null) return;Queue<Node> queue = new LinkedList<>();HashSet<Node> set = new HashSet<>();queue.add(node);set.add(node);while(!queue.isEmpty()){Node cur = queue.poll();/*  具体的处理逻辑（宽搜一般是结点入队列后再处理）*/for(Node next: cur.nexts){if(!set.contains(next)){//如果set中没有，那么说明这个next结点没有被访问过queue.add(next);//扔到队列里set.add(next);//并且标记访问}}}
}public static void dfs(Node node){if(node==null) return;Stack<Node> stack = new Stack<>();HashSet<Node> set = new HashSet<>();stack.add(node);set.add(node);/*具体的处理逻辑（深搜一般是结点入栈前就进行处理）*/while(!stack.isEmpty()){Node cur = stack.pop();for(Node next:cur.nexts){if(!set.contains(next)){stack.push(cur);//在这里需要把cur和next两个结点同时入栈是因为stack.push(next);//想在栈里保持深度搜索的路径。这次搜索相比于上一次搜索，在栈中就多了一个next结点。set.add(cur);set.add(next);/*具体的处理逻辑 */break;//之所以立马break是因为深搜每次只走一步，不像宽搜每次走一层。}}}
}

深拷贝实现（dfs+bfs实现）

见本人另一篇博客http://t.csdnimg.cn/LgIZp

拓扑排序

因为拓扑排序是一定没有环的，那么就一定存在至少一个入度为0的点，我们将这个（些）点放入队列。以这个（其中一个）点为起点出发。每次删掉该点出度相连的直接边，那么就肯定会有新的入度为0的点产生，然后放入队列。那么入队的顺序就是拓扑排序的顺序。

public static List<Node> top(Graph graph){HashMap<Node,Integer> inMap = new HashMap<>();//Node为某一个结点，Integer为该结点剩余的入度Queue<Node> zeroInQueue = new LinkedList<>();//专门存放入度为0的结点的队列。for(Node node: graph.nodes.values()){inMap.put(node, node.in);if(node.in==0) zeroInQueue.add(node);}//第一次循环后，找出了所有入度为0的点放入了队列。List<Node> result = new ArrayList<>();while(!zeroInQueue.isEmpty()){Node cur = zeroInQueue.poll();result.add(cur);for(Node next:cur.nexts){int newin = inMap.get(next)-1;//注意不是next.in-1，因为graph中的入度是不更新的，只有inMap的入度是更新的inMap.push(next,newin);if(newin==0) zeroInQueue.add(next);}}return result;
}

自己留档用

public static void top(Graph graph){if(graph.nodes==null) return null;Queue<Node>queue = new LinkedList<>();for(Node node:graph.nodes.values()){if(node.from==0){//找到入度为0的点/*具体的处理逻辑*/queue.add(node);}}while(!queue.isEmpty()){Node cur = queue.poll();for(Node next:cur.nexts){next.in--;}for(Node node:graph.nodes.values()){if(node.from==0){queue.add(node);}}}
}

最小生成树MST

生成树的定义：

一个连通图的生成树是一个极小的连通子图，它包含图中全部的n个顶点，但只有构成一棵树的n-1条边。
生成树的属性：

一个连通图可以有多个生成树；
一个连通图的所有生成树都包含相同的顶点个数和边数；
生成树当中不存在环；
移除生成树中的任意一条边都会导致图的不连通；
在生成树中添加一条边会构成环。
对于包含n个顶点的连通图，生成树包含n个顶点和n-1条边；
对于包含n个顶点的无向完全图最多包含 n^（n−2）棵生成树。

最小生成树的定义：

所谓一个带权图的最小生成树，就是指原图中边的权值之和最小的生成树。即，最小生成树是和带权图联系在一起的；如果仅仅只是非带权的图，只存在生成树。

Prim算法

适合无向图。
Prim算法的时间复杂度为O（n^2），其中n为顶点数。
可以去看看B站懒猫老师的这部分讲解，个人感觉除了表达为了严谨，用了比较多复杂的数学符号，其他都是讲的很好的。https://www.bilibili.com/video/BV1Ua4y1i7tf/

public static class EdgeComparator implements Comparator<Edge>{@Overridepublic int compare(Edge o1, Edge o2){return o1.weight - o2.weight;}
}public static Set<Edge> prim(Graph graph){//1.选择一个不在set里的起始点，加入set，且解锁该点相连的边//2.选择权值最小的边，看终点是否在set里//3.如果不在，说明是新的点，不会构成环，则该点放入结果集和set中，从该点的相连边开始遍历//4.如果在，说明不是新的点，跳过该点PriorityQueue<Edge> queue = new PriorityQueue<>(new EdgeComparator());//存储边的小根堆，即优先队列Set<Edge> result = new HashSet<>();//存储结果HasSet<Node> set = new HashSet<>();//用来判断是否是新的点 /*为了避免该图是多个不连通的子图组合而成的，然后题目让我们求最小生成森林，所以需要遍历，如果确定是只有一个连通子图，那么可以去掉循环，可以见待会展示的图。1.随便选择一个起始点，加入set，解锁该点相连的边*/for(Node node:graph.nodes.values()){if(!set.contains(node)){set.add(node);for(Edge edge:node.edges){queue.add(edge);}while(!queue.isEmpty()){Edge edge = queue.poll();Node toNode = edge.to;//2.选择权值最小的边，看终点是否在set里if(!set.contains(toNode)){//3.如果不在，说明是新的点，不会构成环，则该点放入结果集和set中，从该点的相连边开始遍历set.add(toNode);result.add(edge);for(Edge edge:toNode.edges){queue.add(edge);}}}}}
}

注意点1：最小生成森林

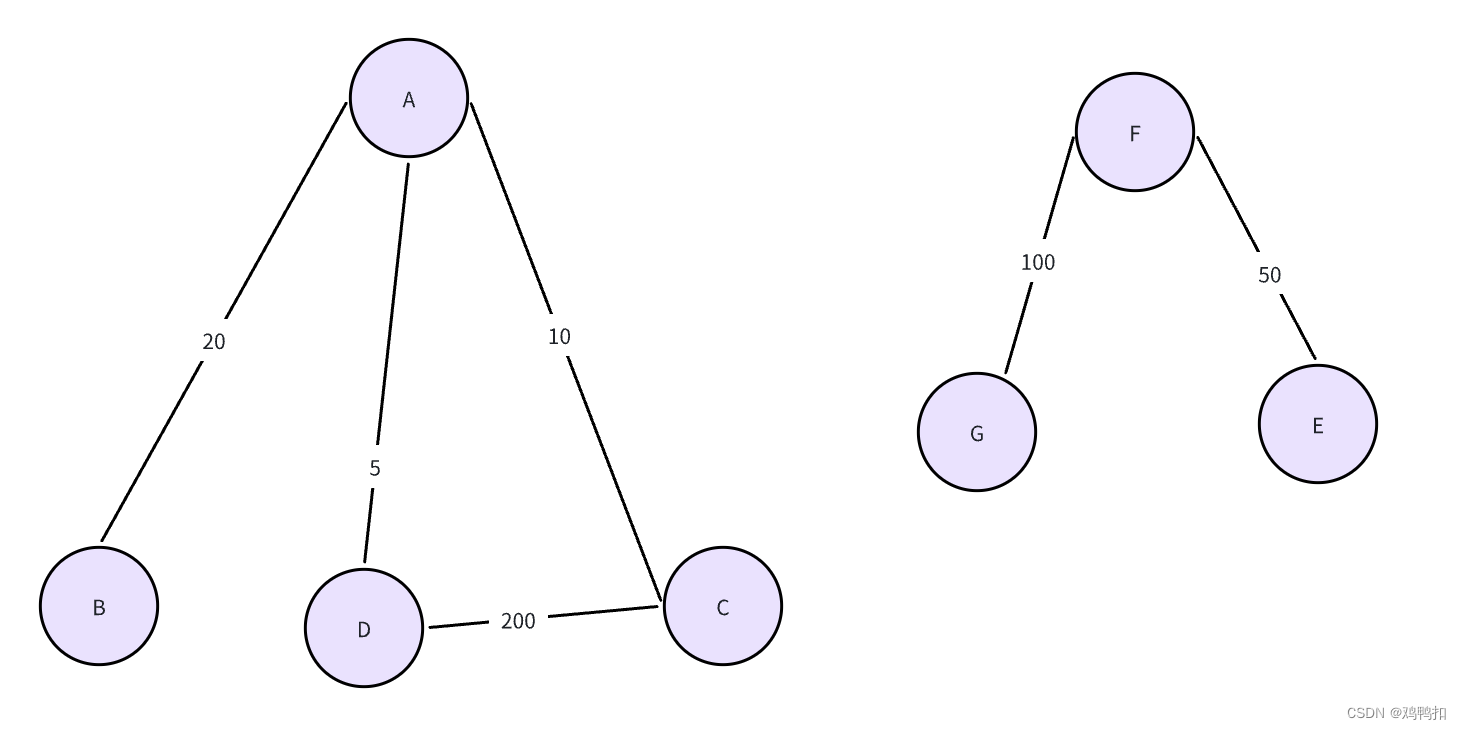
在这里插入图片描述

像是如上图片，A到G的七个点一共是一个大图，但是左边的A到D算是一个子图，右边的E到G算是一个子图。这两个子图之间是相互不连通的。那么我们如果要想得到这个大图的最小生成森林，也是互相不连通的两部分组成的，如下：
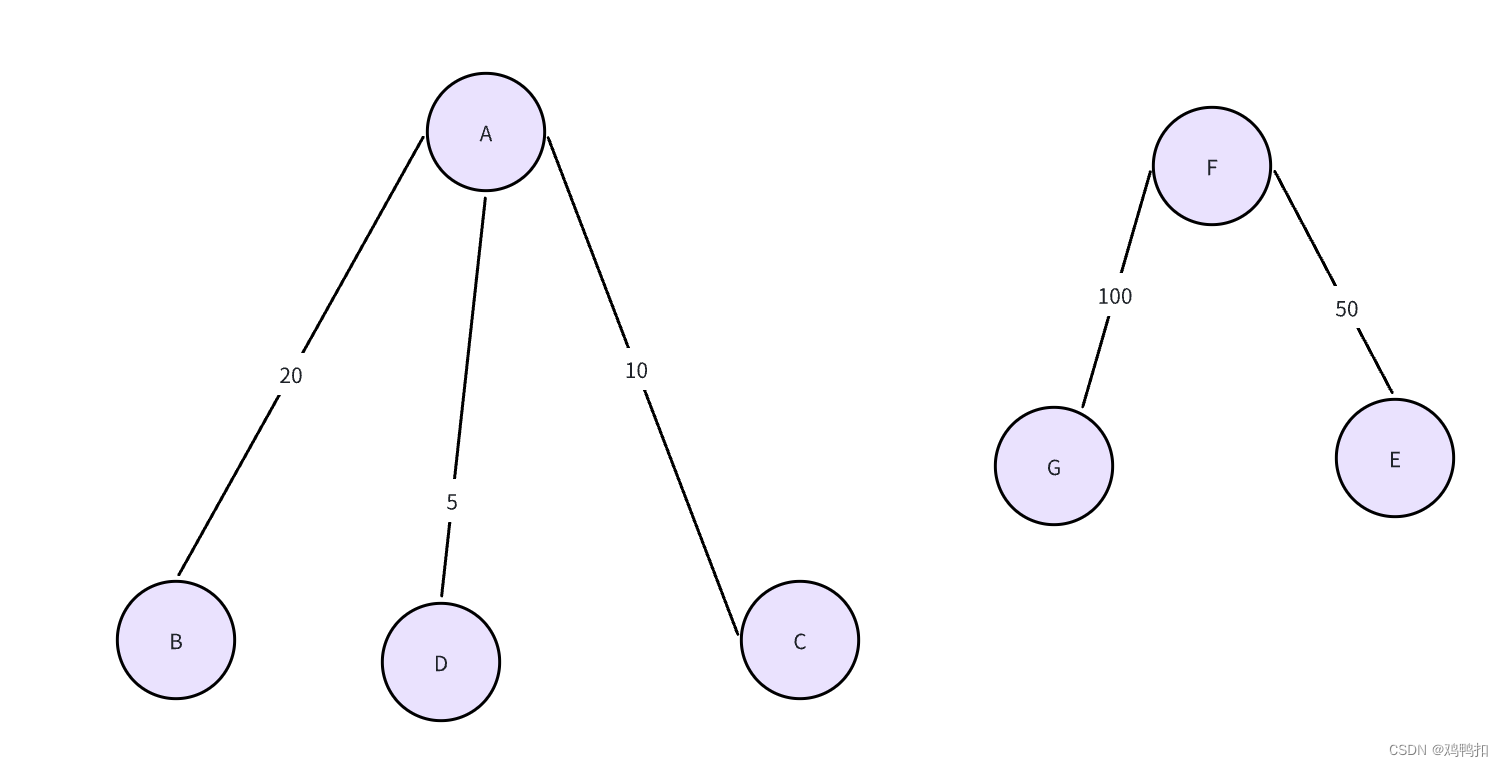
在这里插入图片描述
那么此时我们就需要一个外层循环来确保遍历到所有子图。

Kruskal算法

适合有向无环图。

板子

public static class EdgeComparator implements Comparator<Edge>{@Overridepublic int compare(Edge o1, Edge o2){return o1.weight - o2.weight;}
}public static Set<Edge> kruskal(Graph graph){//1.将每个点作为一个单独的集合//2.将边按照权值从小到大排序//3.依次遍历边，判断起点和终点的集合是否是一个集合//4.如果不是一个集合，将起点和终点的集合合并为一个集合//5.如果是一个集合，说明会构成环，则跳过这条边和边的起点和终点UnionFind unionFind = new UnionFind();//1.unionFind.makeSets(graph.nodes.values());//2.PriorityQueue<Edge> queue = new PriorityQueue<>(new EdgeComparator());for(Edge edge: graph.edges){queue.add(edge);}Set<Edge> result = new HashSet<>();while(!queue.isEmpty()){Edge edge = queue.poll();if(!unionFind.isSameSet(edge.from, edge.to)){result.add(edge);unionFind.union(edge.from, edge.to);}}return result;
}

Dijkstra算法

适用于没有累加后权值为负数的环的图（也可以直接粗暴地大范围地认为权值为负数的图不适合）
感觉这里左神没有讲的很好，可以去看b站懒猫老师讲的。

板子

初代板子找寻距离最短的且没有被遍历到的节点的函数是通过循环实现的，复杂度较高。但是可以用堆优化，不过不是系统提供的堆算法，因为系统提供的堆不支持给过的节点的值修改的操作，所以需要自己手写实现堆。

public static HashMap<Node, Integer> Dijkstra(Node head){HashMap<Node,Integer>distanceMap = new HashMap<>();//从head点出发，到达每个节点的最短距离（包含head自身）HashSet<Node> set = new HashSet<>();//节点是否已经遍历过distanceMap.put(head,0);Node minNode = selectNode(distanceMap, set);while(minNode!=null){int mindistance = distanceMap.get(minNode);//当前从head出发，到达最近点的最短距离for(Edge edge:minNode.edges){//最近点的邻边Node toNode = edge.to;//最近点直接相连的节点if(!distanceMap.containsKey(toNode))//如果这个最近点直接相连的节点没有在distanceMap中出现过//那么说明这条最近点的邻边是新遍历到的边distanceMap.put(toNode,mindistance+edge.weight);//我们需要把这条新边的新点距离head的距离加入distanceMap中else{            distanceMap.put(edge.to,Math.min(distanceMap.get(toNode),mindistance+edge.weight))}//如果这个节点不是新遍历到的，那么就需要看是否需要更新我们之前的最短距离}set.add(minNode);minNode = selectNode(distanceMap, set);}return distanceMap;
}public static Node selectNode(HashMap<Node,Integer> distanceMap, HashSet<Node> set){int minDistance = Integer.MAX_VALUE;Node minNode = null;//将distanceMap中每个节点拿出来，找出距离最短的且没有被遍历到的节点for(Entry<Node,Integer> entry: distanceMap.entrySet()){Node node = entry.getKey();int distance = entry.getValue();if(!set.containsKey(node)&&distance<minDistance){minDistance = distance;minNode = node;}}return minNode;
}