1 雅各布斯塔尔序列
雅各布斯塔尔序列是一个与斐波那契序列类似的加法序列,由递归关系Jn=Jn-1+2Jn-2定义,初始项J0=0,J1=1。序列中的一个数字称为雅可布沙尔数。它们是卢卡斯序列Un(P,Q)的一种特殊类型,其中P=1,Q=-2。
第一个雅各布斯塔尔数字是:
0, 1, 1, 3, 5, 11, 21, 43, 85, 171, 341, 683, 1365, 2731, 5461, 10923, 21845, 43691, ……
Jacobsthal数由递推关系定义:
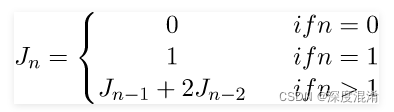
2 雅各布斯塔尔-卢卡斯数
雅各布斯塔尔-卢卡斯数数表示互补卢卡斯序列Vn(1,-2)。它们满足与雅各布斯塔尔数相同的递归关系,但具有不同的初始值:
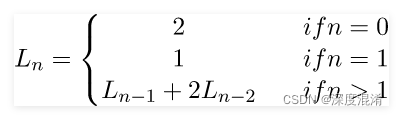
Jacobsthal Number计算结果:
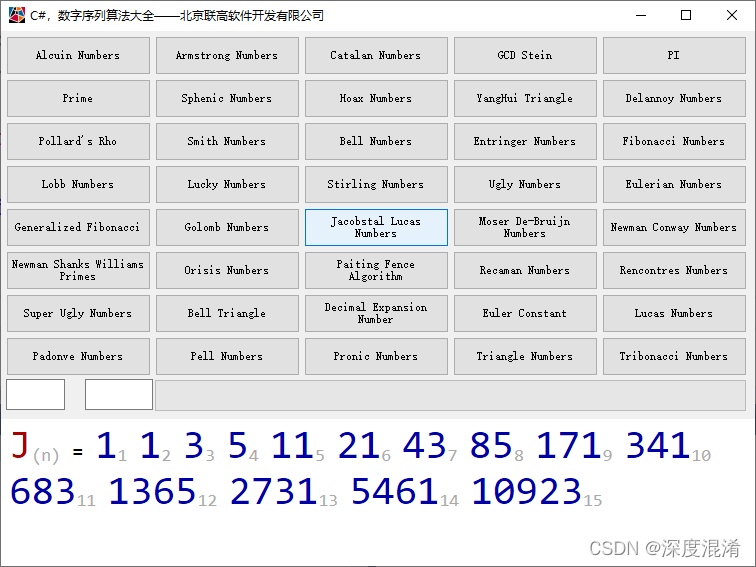
Jacobsthal Lucas Number 计算结果:

3 文本格式源程序
using System;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class Number_Sequence
{
public static int Jacobsthal_Number(int n)
{
if (n == 0)
{
return 0;
}
// base case
if (n == 1)
{
return 1;
}
return Jacobsthal_Number(n - 1) + 2 * Jacobsthal_Number(n - 2);
}
public static int Jacobsthal_Lucas_Number(int n)
{
if (n == 0)
{
return 2;
}
if (n == 1)
{
return 1;
}
int a = Jacobsthal_Lucas_Number(n - 1);
int b = 2 * Jacobsthal_Lucas_Number(n - 2);
return (a + b);
}
public static int Jacobsthal_Number_Second(int n)
{
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++)
{
dp[i] = dp[i - 1] + (2 * dp[i - 2]);
}
return dp[n];
}
public static int Jacobsthal_Lucas_Number_Second(int n)
{
int[] dp = new int[n + 1];
dp[0] = 2;
dp[1] = 1;
for (int i = 2; i <= n; i++)
{
dp[i] = dp[i - 1] + (2 * dp[i - 2]);
}
return dp[n];
}
}
}
——————————————————————
POWER BY TRUFFER.CN
4 代码格式源代码
using System;namespace Legalsoft.Truffer.Algorithm
{public static partial class Number_Sequence{public static int Jacobsthal_Number(int n){if (n == 0){return 0;}// base caseif (n == 1){return 1;}return Jacobsthal_Number(n - 1) + 2 * Jacobsthal_Number(n - 2);}public static int Jacobsthal_Lucas_Number(int n){if (n == 0){return 2;}if (n == 1){return 1;}int a = Jacobsthal_Lucas_Number(n - 1);int b = 2 * Jacobsthal_Lucas_Number(n - 2);return (a + b);}public static int Jacobsthal_Number_Second(int n){int[] dp = new int[n + 1];dp[0] = 0;dp[1] = 1;for (int i = 2; i <= n; i++){dp[i] = dp[i - 1] + (2 * dp[i - 2]);}return dp[n];}public static int Jacobsthal_Lucas_Number_Second(int n){int[] dp = new int[n + 1];dp[0] = 2;dp[1] = 1;for (int i = 2; i <= n; i++){dp[i] = dp[i - 1] + (2 * dp[i - 2]);}return dp[n];}}
}

— 引入密集连接卷积网络DenseNet)

用法总结)
)





)





- Yarn)
)
