文章目录
- 1 贝叶斯定理相关公式
- 2 朴素贝叶斯算法
- 2.1 朴素贝叶斯算法推导
- 2.2 朴素贝叶斯算法流程
- 3 高斯朴素贝叶斯
- 4 伯努利朴素贝叶斯
- 5 多项式朴素贝叶斯
- 6 贝叶斯网络
- 6.1 最简单的一个贝叶斯网络
- 6.2 全连接贝叶斯网络
- 6.3 “正常”贝叶斯网络
- 6.4 实际贝叶斯网络:判断是否下雨
- 6.5 贝叶斯网络判定条件独立-01
- 6.6 贝叶斯网络判定条件独立-02
- 6.7 贝叶斯网络判定条件独立-03
1 贝叶斯定理相关公式
-
**先验概率P(A):**在不考虑任何情况下,A事件发生的概率。
-
**条件概率P(B|A):**A事件发生的情况下,B事件发生的概率。
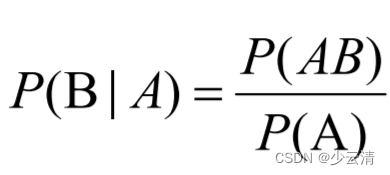
-
**后验概率P(A|B):**在B事件发生之后,对A事件发生的概率的重新评估。
-
**全概率:**如果A和A’构成样本空间的一个划分,那么事件B的概率为:A和A’的概率分别乘以B对这两个事件的概率之和。
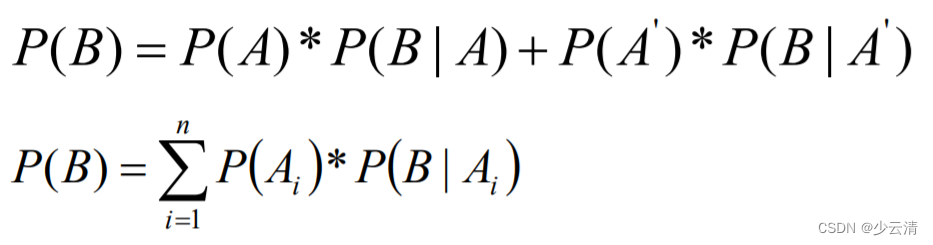
-
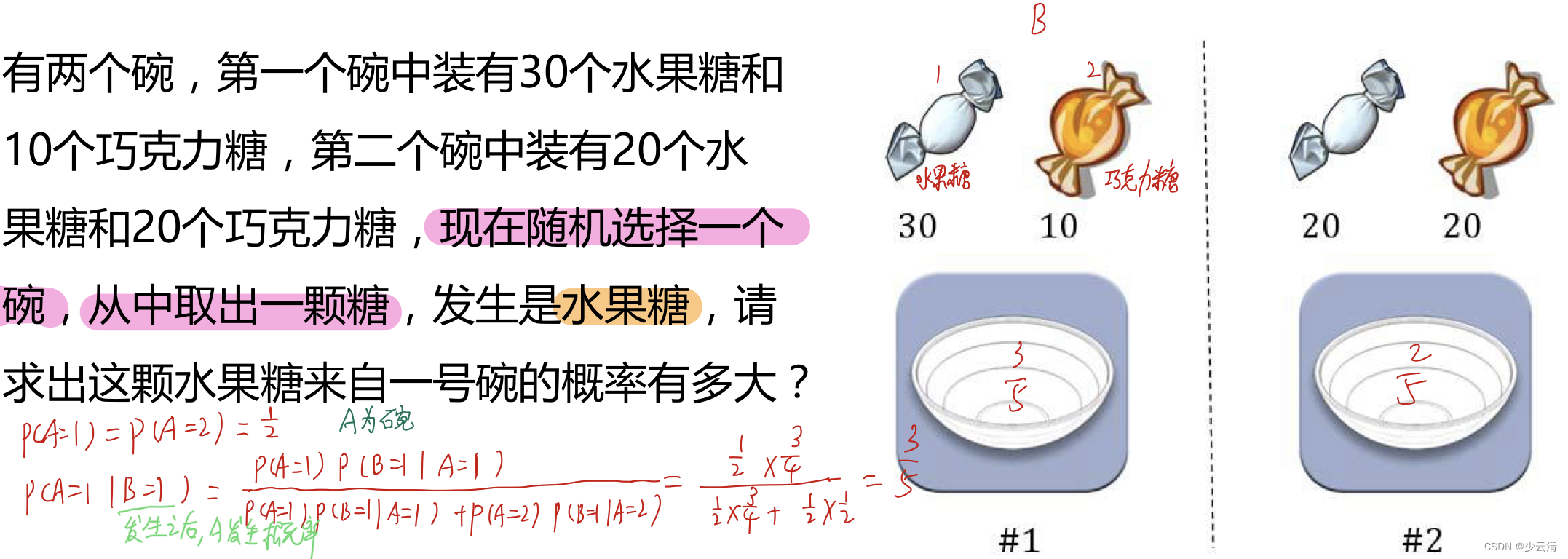
基于条件概率的贝叶斯定律数学公式
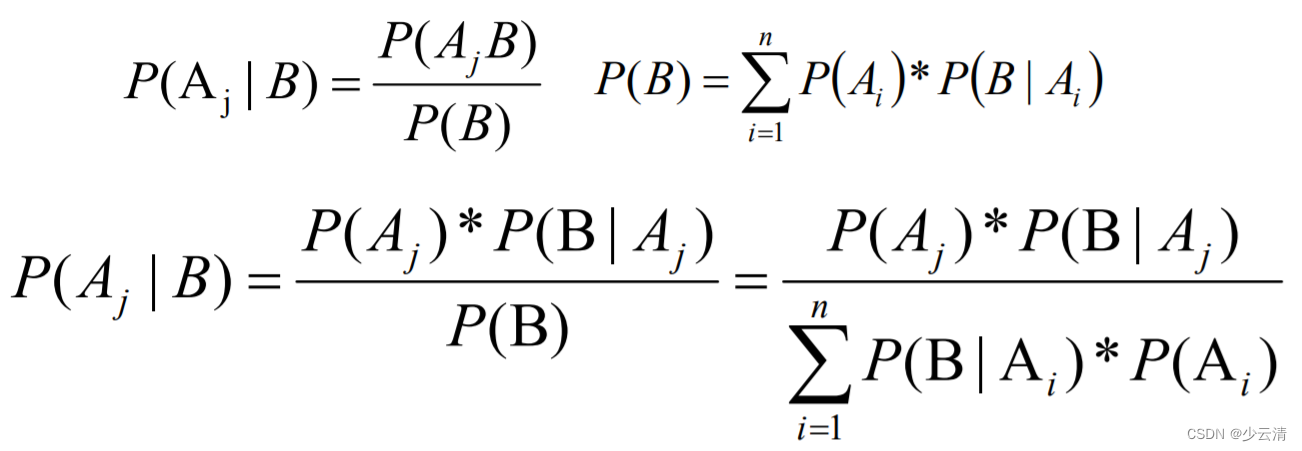
2 朴素贝叶斯算法
- 朴素贝叶斯(Naive Bayes, NB)是基于“特征之间是独立的”这一朴素假设,应用贝叶斯定理的监督学习算法
- 对应给定的 样本X 的特征向量x1 ,x2 ,…,xm;该 样本X 的 类别y 的概率可以由贝叶斯公式得到:
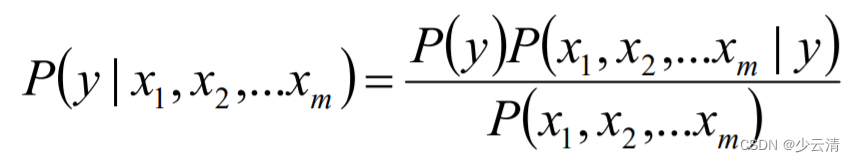
2.1 朴素贝叶斯算法推导
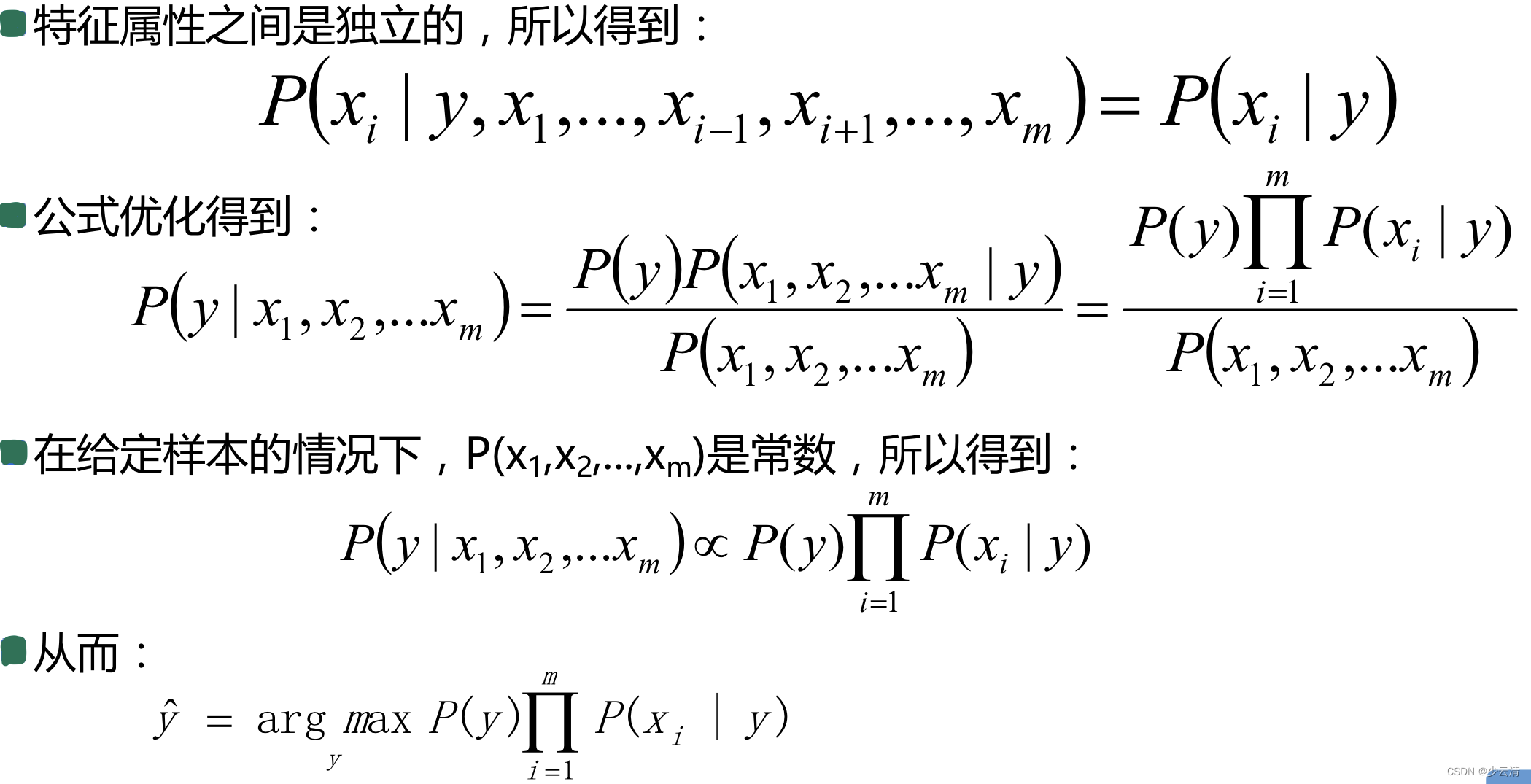
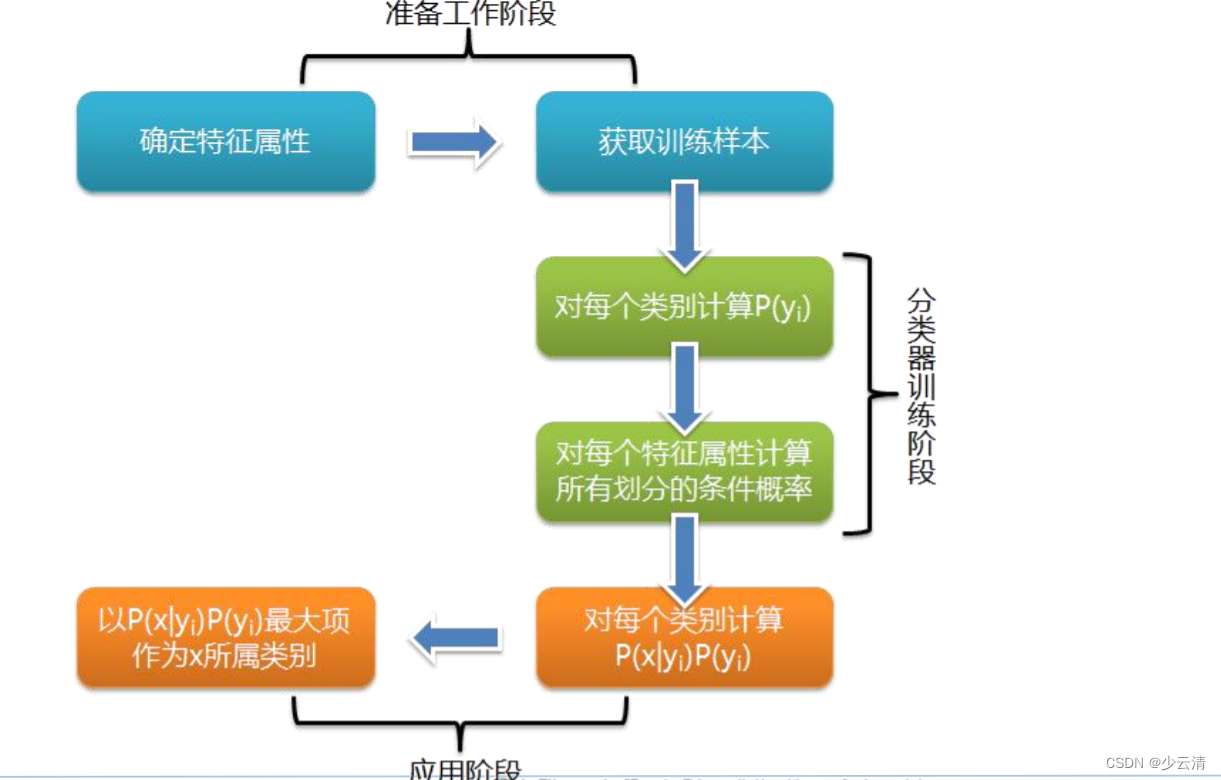
2.2 朴素贝叶斯算法流程
朴素贝叶斯算法流程/定义如下:
- 设x={x1 ,x2 ,…,xm}为待分类项,其中xi为x的一个特征属性。
- 类别集合为C={y1 ,y2 ,…,yn }。
- 分别计算P(y1 |x),P(y2 |x),…,P(yn |x)的值(贝叶斯公式)。
- 如果P(yk |x)=max{P(y1 |x),P(y2 |x),…,P(yn |x)},那么认为x为yk类型。
3 高斯朴素贝叶斯
- Gaussian Naive Bayes是指当特征属性为连续值时,而且分布服从高斯分布,那么在计算P(x|y)的时候可以直接使用高斯分布的概率公式:
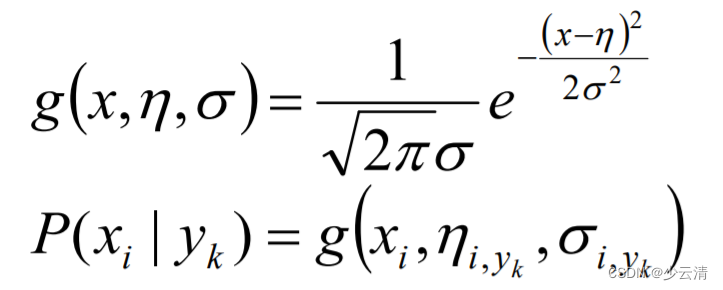
- 因此只需要计算出各个类别中此特征项划分的各个均值和标准差。
4 伯努利朴素贝叶斯
- Bernoulli Naive Bayes是指当特征属性为连续值时,而且分布服从伯努利分布,那么在计算P(x|y)的时候可以直接使用伯努利分布的概率公式:
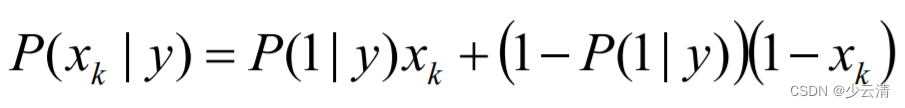
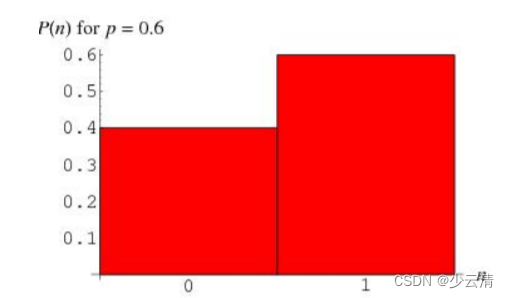
伯努利分布是一种离散分布,只有两种可能的结果。1表示成功,出现的概率为p; 0表示失败,出现的概率为q=1-p;其中均值为E(x)=p,方差为Var(X)=p(1-p)。
5 多项式朴素贝叶斯
- Multinomial Naive Bayes是指当特征属性服从多项分布(特征是离散的形式的时候),从而,对于每个类别y,参数为θy=(θy1,θy2,…,θyn),其中n为特征属性数目,那么P(xi|y)的概率为θyi。
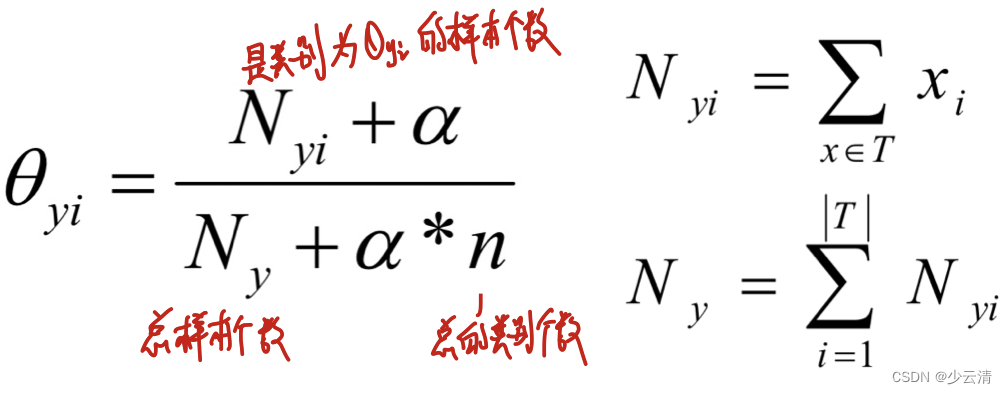
Ny是总样本个数,n是总的类别个数,Nyi是类别为θyi的样本个数,α为平滑值。
当α=1时,称为Laplace平滑,当0<α<1时,称为Lidstone平滑,α=0时不做平滑;平滑的主要作用是可以克服条件概率为0的问题。
6 贝叶斯网络
- 把某个研究系统中涉及到的随机变量,根据是否条件独立绘制在一个有向图中,就形成了贝叶斯网络。
- 贝叶斯网络(Bayesian Network),又称有向无环图模型(directed acyclic graphical model, DAG),是一种概率图模型,根据概率图的拓扑结构,考察一组随机变量{X1 ,X2 ,…,Xn}及其N组条件概率分布(Conditional Probabililty Distributions, CPD)的性质。
- 当多个特征属性之间存在着某种相关关系的时候,使用朴素贝叶斯算法就没法解决这类问题,那么贝叶斯网络就是解决这类应用场景的一个非常好的算法。
- 一般而言,贝叶斯网络的有向无环图中的节点表示随机变量,可以是可观察到的变量,或隐变量,未知参数等等。连接两个节点之间的箭头代表两个随机变量之间的因果关系(也就是这两个随机变量之间非条件独立),如果两个节点间以一个单箭头连接在一起,表示其中一个节点是“因” ,另外一个是“果” ,从而两节点之间就会产生一个条件概率值。
- 注意:每个节点在给定其直接前驱的时候,条件独立于其后继。
- 贝叶斯网络的关键方法是图模型,构建一个图模型我们需要把具有因果联系的各 个变量用箭头连在一起。贝叶斯网络的有向无环图中的节点表示随机变量。连接 两个节点的箭头代表此两个随机变量是具有因果关系的。
- 贝叶斯网络是模拟人的认知思维推理模式的,用一组条件概率以及有向无环图对 不确定性因果推理关系建模。
6.1 最简单的一个贝叶斯网络
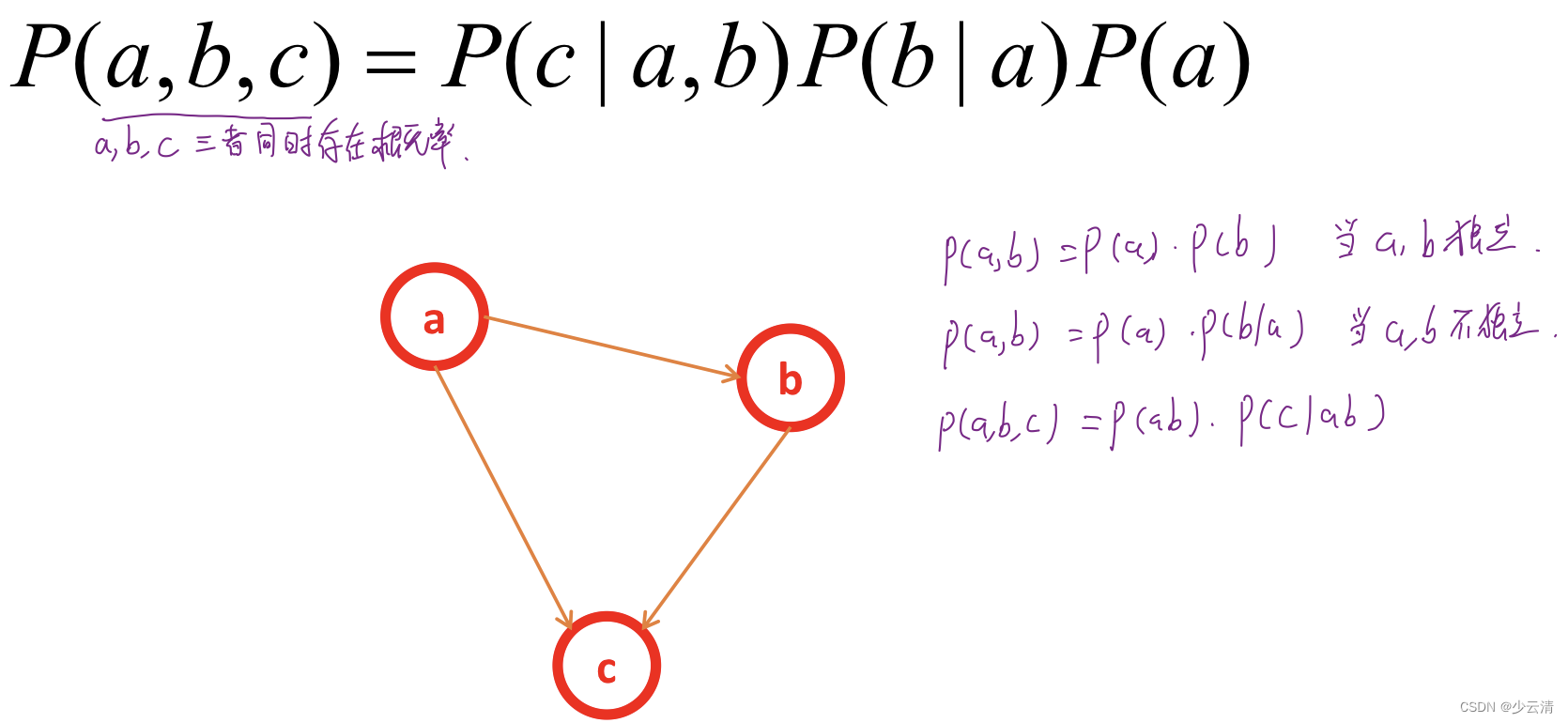
6.2 全连接贝叶斯网络
每一对节点之间都有边连接:
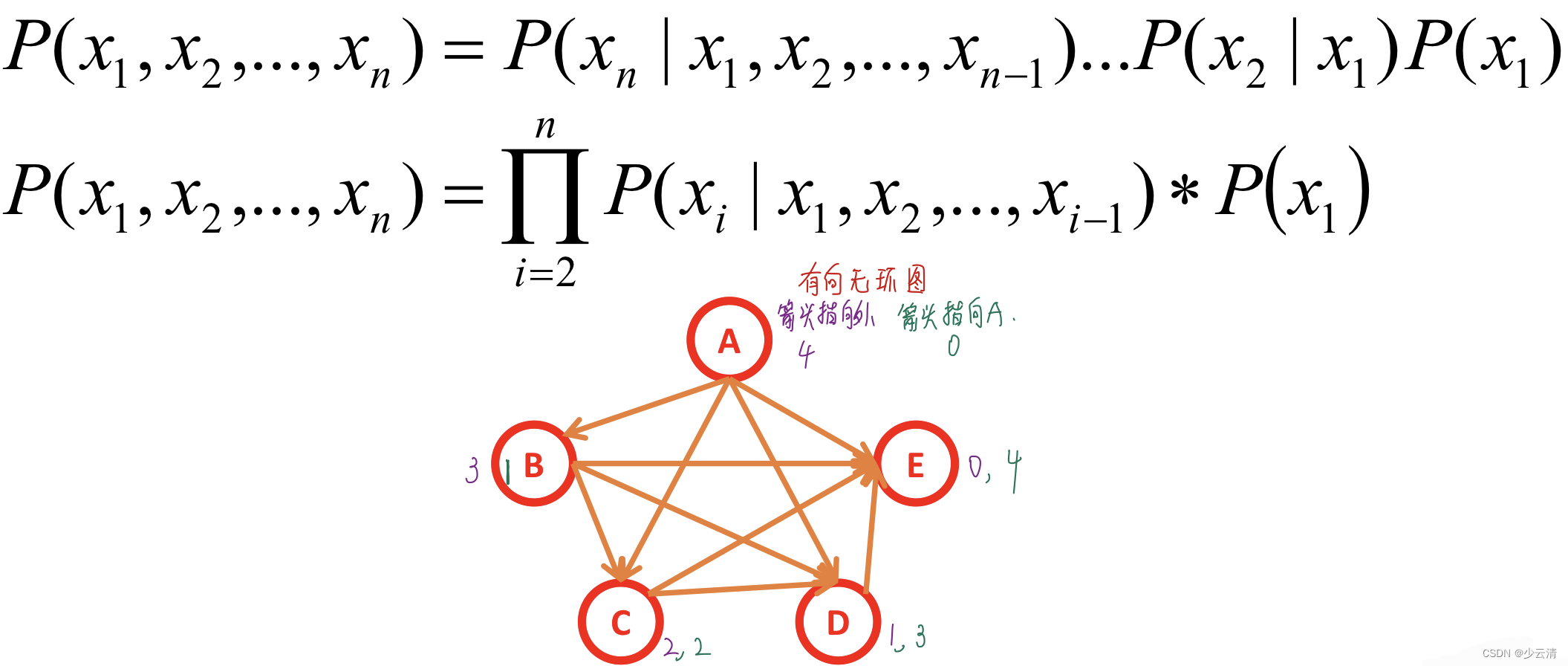
6.3 “正常”贝叶斯网络
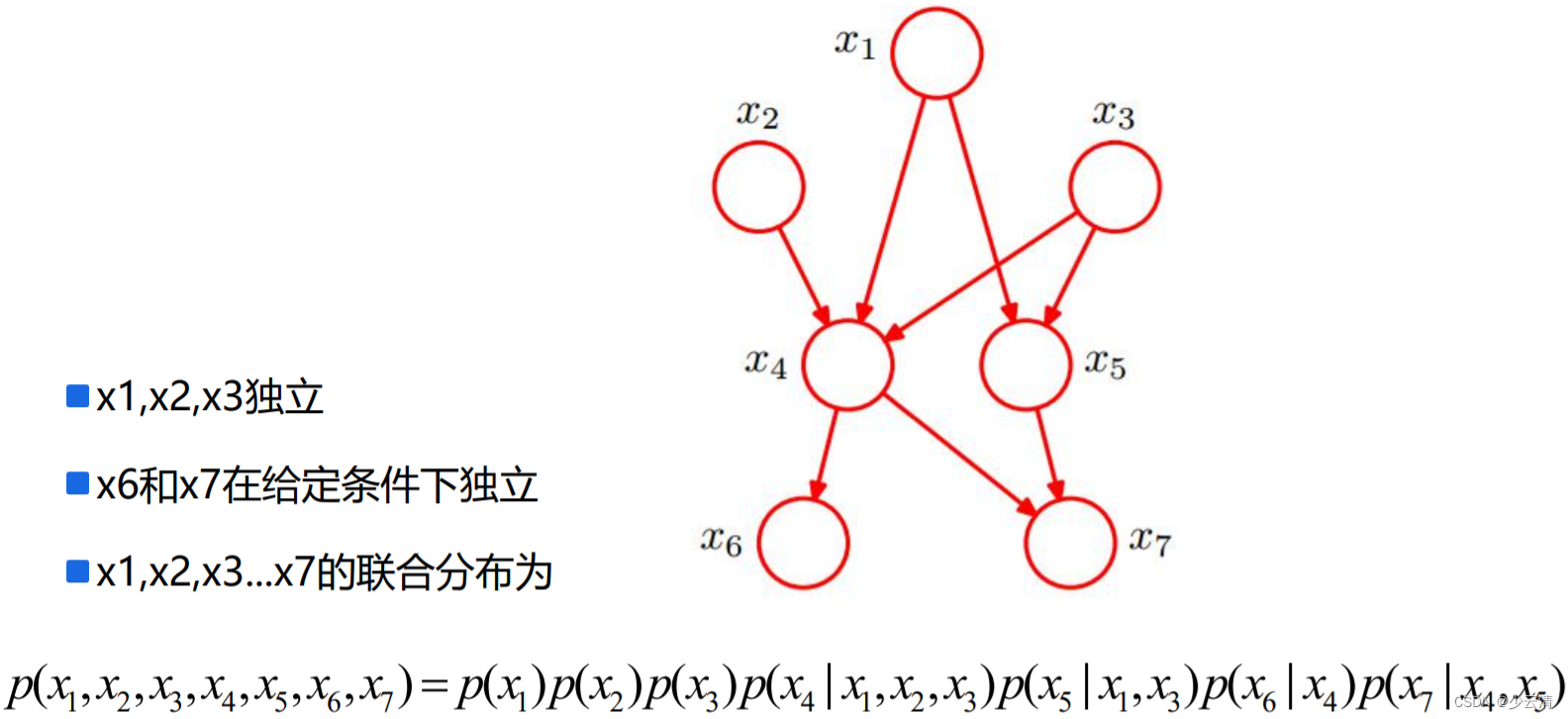
6.4 实际贝叶斯网络:判断是否下雨
有一天早晨,Bruce离开他的房子的时候发现他家花园中的草地是湿的,有两种可能,第一:昨天晚上下雨了,第二:他昨天晚上忘记关掉花园中的喷水器,接下来,他观察他的邻居Joe,发现他家花园中的草地也是湿的,因此,他推断,他家的草地湿了是因为昨天晚上下雨的缘故。
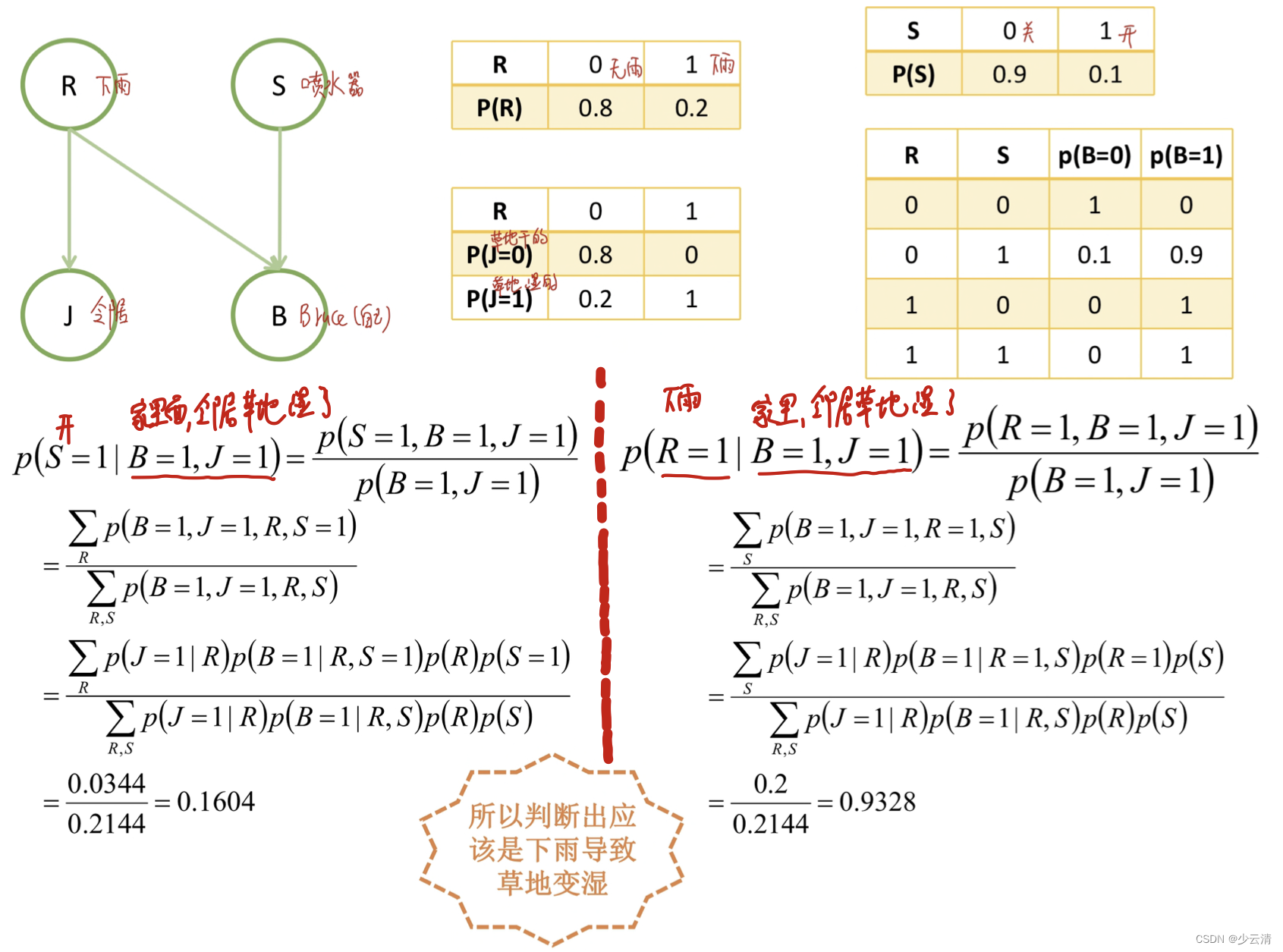
6.5 贝叶斯网络判定条件独立-01

6.6 贝叶斯网络判定条件独立-02
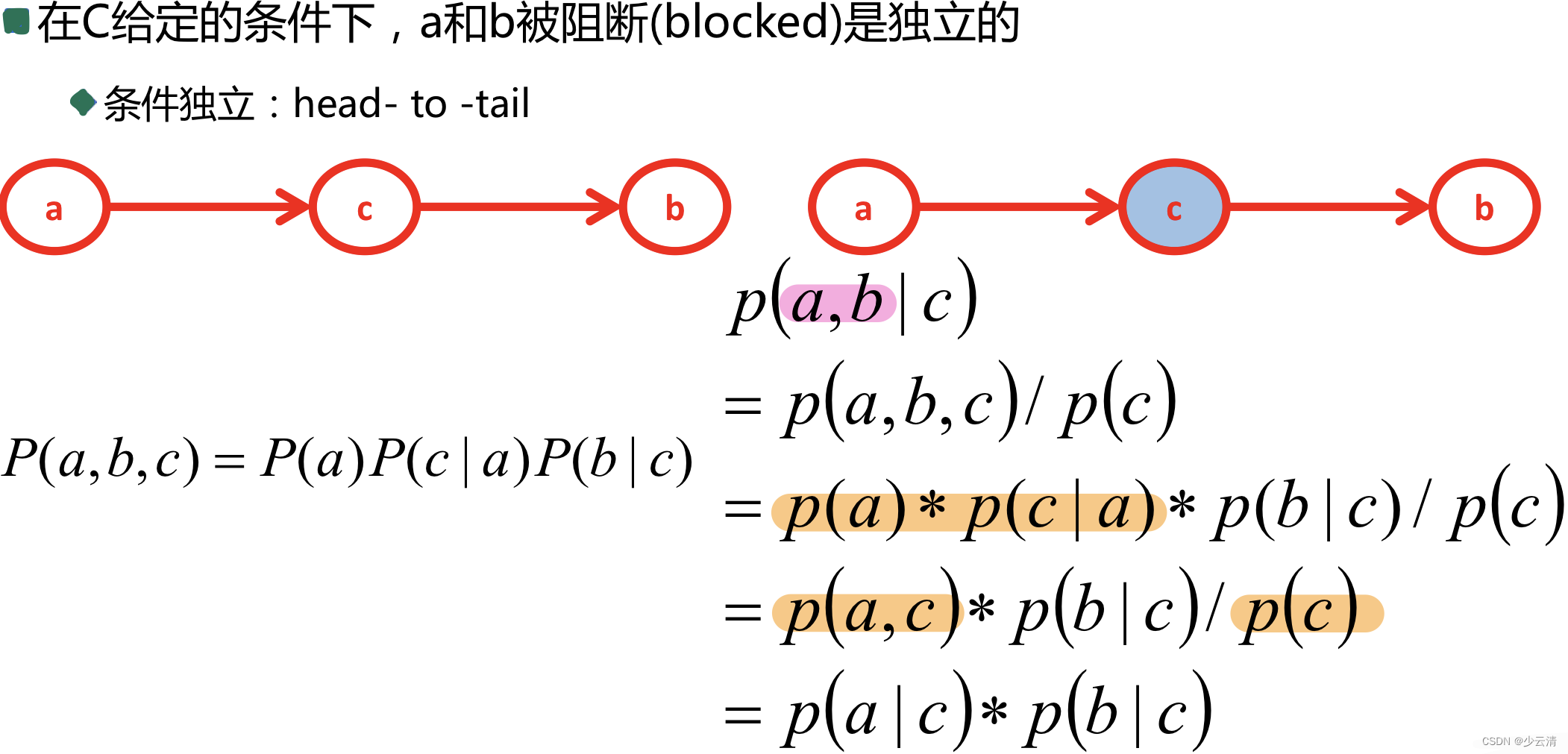
6.7 贝叶斯网络判定条件独立-03

)


)









)


)

)
