作者简介:大家好,我是smart哥,前中兴通讯、美团架构师,现某互联网公司CTO
联系qq:184480602,加我进群,大家一起学习,一起进步,一起对抗互联网寒冬
学习必须往深处挖,挖的越深,基础越扎实!
阶段1、深入多线程
阶段2、深入多线程设计模式
阶段3、深入juc源码解析
阶段4、深入jdk其余源码解析
阶段5、深入jvm源码解析
码哥源码部分
码哥讲源码-原理源码篇【2024年最新大厂关于线程池使用的场景题】
码哥讲源码【炸雷啦!炸雷啦!黄光头他终于跑路啦!】
码哥讲源码-【jvm课程前置知识及c/c++调试环境搭建】
码哥讲源码-原理源码篇【揭秘join方法的唤醒本质上决定于jvm的底层析构函数】
码哥源码-原理源码篇【Doug Lea为什么要将成员变量赋值给局部变量后再操作?】
码哥讲源码【你水不是你的错,但是你胡说八道就是你不对了!】
码哥讲源码【谁再说Spring不支持多线程事务,你给我抽他!】
终结B站没人能讲清楚红黑树的历史,不服等你来踢馆!
打脸系列【020-3小时讲解MESI协议和volatile之间的关系,那些将x86下的验证结果当作最终结果的水货们请闭嘴】
引言
在上篇文章《再不会"降维打击"你就Out了!》中,提到了递归算法的两个局限性。本文给出解决方案——动态编程。如果说"递归算法"是圣剑的话,那么"动态编程"就是圣衣。两者加持,你便可以爆发究极小宇宙:)

递归算法局限性详细分析
局限性1(适用性问题):
如果“降维”前的状态集合并不方便用“降维”后的状态集合表示,即状态转移函数不好求,那么该场景使用递归不一定恰当。
下面举个例子来说明:
有两个集合A和B,A中有n个元素,B中也有n个相同元素,将A中的元素通过映射f,映射到B中的元素,映射f满足:f(f(x))=f(x),求这样的不同映射有多少种。
根据在《再不会"降维打击"你就Out了!》中讲到的递归应用的优化套路,很容易看出,规模因子就是n,关键要求的就是状态转移函数g:f(n-1)->f(n)。
f(n-1)表示A和B各有n-1个元素时,不同映射的种数;
f(n)表示A和B各有n个元素时,不同映射的种数。
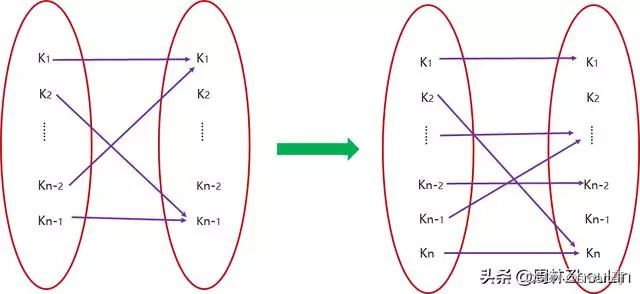
上图左侧表示的就是f(n-1)对应的一种情况,右侧表示的就是f(n)对应的一种情况。
在上面图示的情况中:
元素个数等于n-1时,A中的元素K2映射到B中的元素Kn-1;
但是元素个数等于n时,A中的元素K2映射到B中的元素Kn,此时映射的种数等价于下图映射的种数:
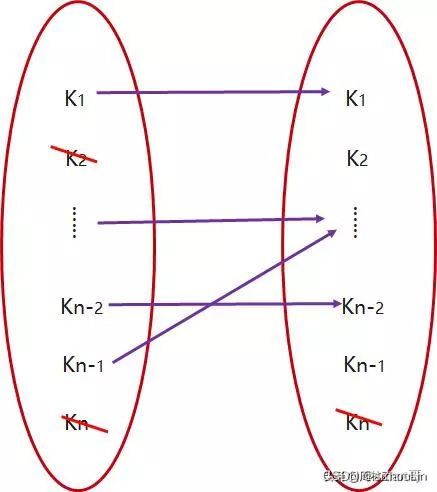
这是一个n-2个元素到n-1个元素的映射,显然它的值不一定等于f(n-1)。
换言之,在本例中,f(n)并不方便用f(n-1)来表示,即状态转移函数g:f(n-1)->f(n)不好求。
原因就是:
问题规模变化时,“形状”变了——从(n-1)->(n-1)变成了(n-2)->(n-1)——直观地说,从“正方形”变成了“梯形”。
如果仍然要用递归来解,那么就需要引入中间态辅助函数,计算“梯形”的函数值。
局限性2(重复计算问题):
在直接递归的过程中部分函数值会被重复计算
为了避免重复计算,一个直接而朴素的想法就是:引入中间态辅助函数,将算过的函数值存下来,递归时再次遇到该函数时,直接从保存结果中取出来。
从上面对两个局限性的分析可以看出:优化递归的方法就是引入中间态辅助函数,保存中间态结果。
这种方法就叫做“动态编程”。
自顶向下 vs. 自底向上
很明显,保存中间态结果,有两种方式——自顶向下或者自底向上。
还是拿《再不会"降维打击"你就Out了!》中的爬台阶的例子来讲。
最终的状态转移函数表达式如下:
当n>=4时:
f(n)=f(n-1)+f(n-2)+f(n-3)
当1<=n<4时:f(n)=n
当n<1时:f(n)=0
递归的自然方向就是自顶向下。递归的同时,首先查一下保存函数值的线性表,如果查得到,那么就直接“拿来主义”;
如果查不到,那么计算完了函数值之后,也往线性表里保存结果,这样后面的递归步骤如果用得上的话,就节省计算时间了。
这里的线性表是不是有点像“备忘录”呢?所以这个方法也称作“备忘录法”
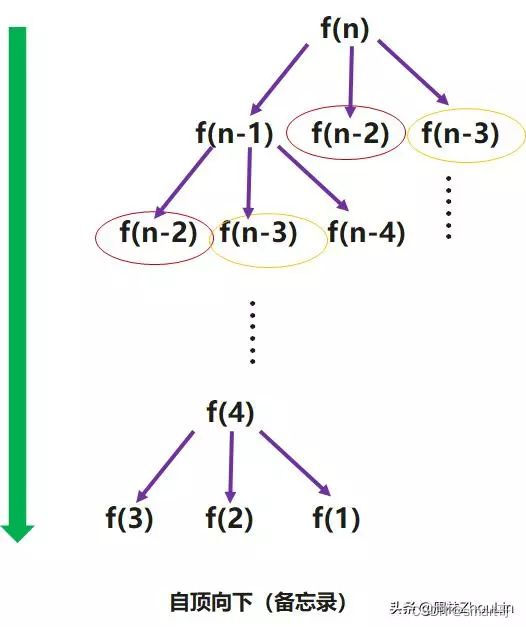
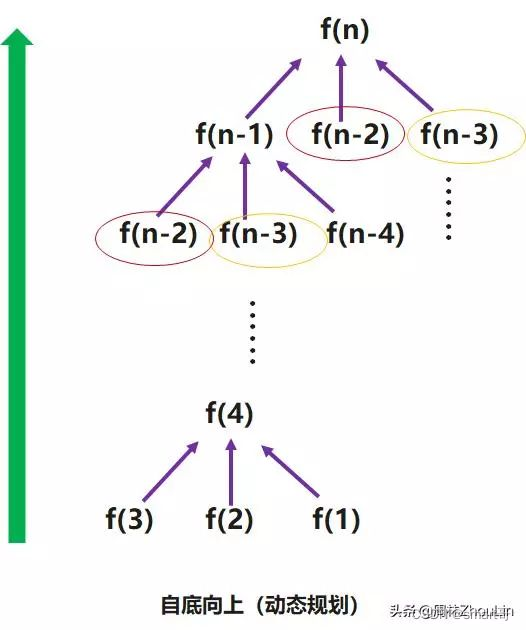
下面再来看看自底向上。我们逆着递归自然展开的方向,根据状态转移函数,一边查表一边从底部向上逐步计算函数值,并将新计算出来的值也保存到线性表中,供更高层的函数值计算时使用。这种方法就叫做“动态规划”。
由于“动态规划”是逆着递归自然展开的方向,所以写出开的程序结构不再是递归形式,而是递归展开的反向形式——循环结构。
进一步优化
细心的同学肯定发现了:无论是“备忘录法”还是“动态规划”,都要保存所有的中间结果,这必将导致空间复杂度极大。
那么如何优化呢?
还是拿上面的爬台阶的例子来说明。根据上面的树状图示,显然每次求当前层的函数值时,只会用到紧邻的下一层的几个函数值,这意味着更深层的函数值都没有用了,可以舍去、释放内存。
换言之,无论是使用“备忘录法”还是“动态规划”,都要分析状态转移函数,看看“降维”前后到底涉及哪些状态,不在这个状态集合里的函数值都可以舍去、释放内存。


分支的绝对干净)




)

)


(tree转换为List))



 算法)


