题目描述

题目思路
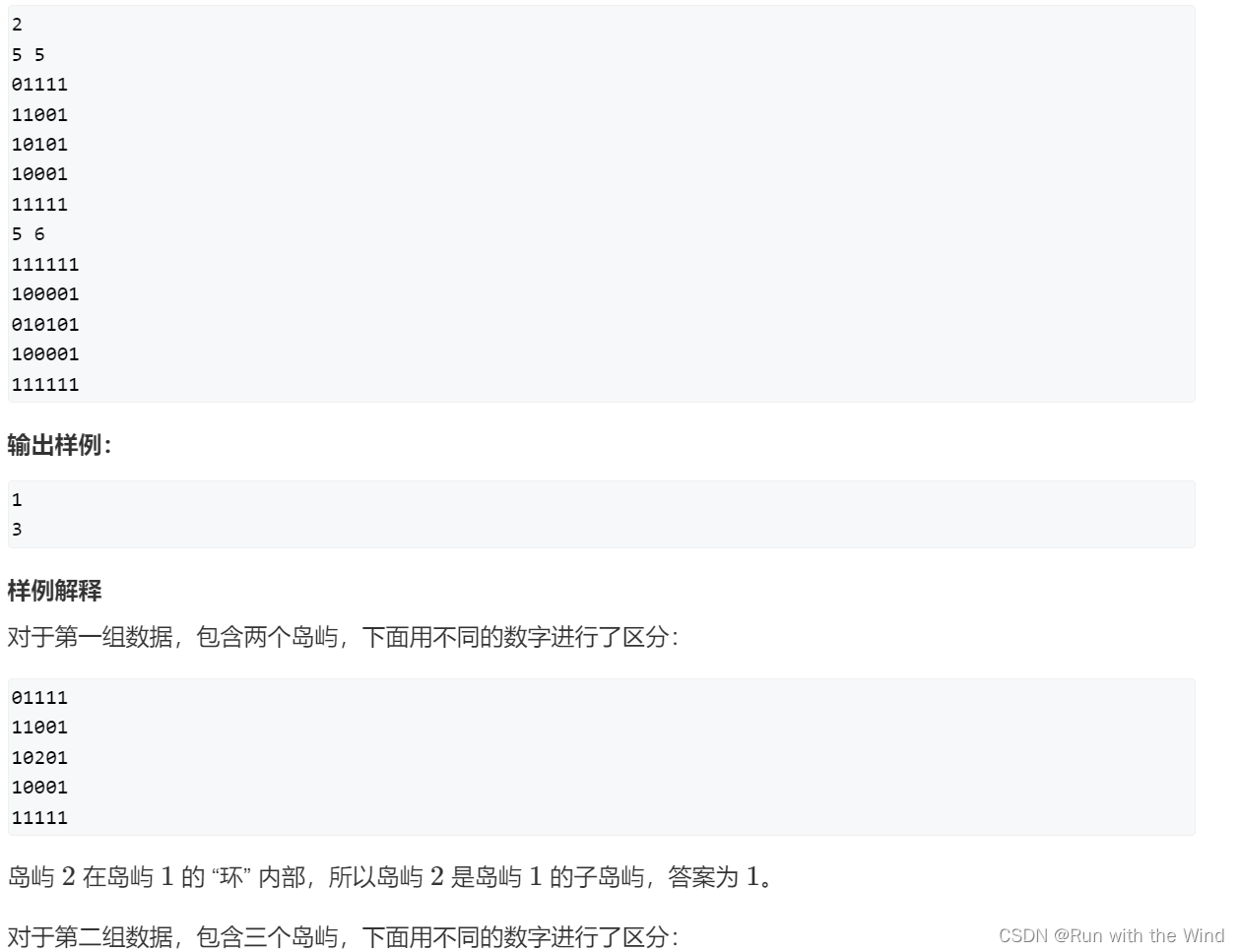
题目乍一看类似于“水坑个数问题”,是对陆地块进行DFS,上下左右4个方向分别对应了四种状态转移,每块陆地进行搜索后变成海洋,最终搜索次数就是岛屿个数。
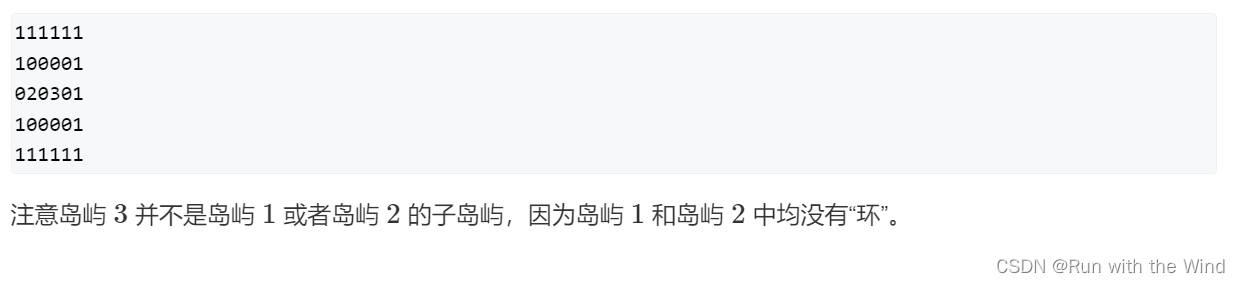
但在子岛屿存在的情况下,需要先对海洋块进行DFS,由于不被岛屿包围的海洋能够通过八个方向流往地图边界,若最终没有能够流到边界,则说明这片水域是在某块岛屿内部,将水域填充成陆地,这样就能让每片大岛屿与它的所有子岛屿连成一片,消除所有子岛屿。然后再进行上述的搜索就能统计出不包含子岛屿的岛屿个数了。
我的代码
值得注意的是,一开始我的地图存储数组是int类型的,但是在输入01串的时候,本来代表地图一行的011101会被理解成一个整数,为了按位读取数据,需要将数组的类型改成char类型。
另外重要的一点,在进行DFS或BFS时必须给已经搜索过的区域进行标记,在本就储存了信息的数组里不方便再添加标记,较好的方法说建立一个相同大小的数组用于储存是否已搜索的信息。由于我的代码总共用了三次DFS:前两次搜索的方向数为8,最后一次搜索方向数为4,总共的时间复杂度约为,很有优化的空间,不过还是通过了所有测试点。
#include <iostream>
#include <algorithm>
using namespace std;
char map[52][52];
int view[52][52];
int dfs1(int x, int y) { //判断是否连接大海view[x][y] = 1;for (int dx = -1; dx <= 1; dx++) {for (int dy = -1; dy <= 1; dy++) //8方向循环{int nx = x + dx;int ny = y + dy;if (map[nx][ny] == '2') {return 1;}if (map[nx][ny] == '0' && view[nx][ny] == 0) {if (dfs1(nx, ny)) {return 1;}}}}return 0;
}
void dfs2(int x, int y,char f) {if (view[x][y] == 1) {view[x][y] = 0;map[x][y] = f;}for (int dx = -1; dx <= 1; dx++) {for (int dy = -1; dy <= 1; dy++){int nx = x + dx;int ny = y + dy;if (view[nx][ny] == 1) {dfs2(nx, ny,f);}}}
}
void dfs3(int x, int y) {map[x][y] = '0';int dx[4] = { -1,0,0,1 };int dy[4] = { 0,-1,1,0 };for (int i = 0; i < 4; i++) //四方向{int nx = x + dx[i];int ny = y + dy[i];if (map[nx][ny] == '1') {dfs3(nx, ny);}}
}
int main() {int m;int n;int i;int j;int T;cin >> T;//输入组数while (T--) {cin >> m >> n;//赋值for (i = 1; i <= m; i++) {for (j = 1; j <= n; j++){cin >> map[i][j];view[i][j] = 0;}}//地图边界for (i = 0; i <= n+1; i++){map[0][i] = '2';map[m+1][i] = '2';}for (j = 1; j <= m+1; j++){map[j][0] = '2';map[j][n+1] = '2';}//DFS1:寻找子岛屿//DFS2:消除子岛屿for (i = 1; i <= m; i++) {for (j = 1; j <= n; j++){if (map[i][j] == '0') {if (dfs1(i, j)) { //非子岛屿dfs2(i, j, '0');}else {//子岛屿dfs2(i, j, '1');}}}}for (i = 1; i <= m; i++) {for (j = 1; j <= n; j++){if (map[i][j] == '0') {if (dfs1(i, j)) {//非子岛屿dfs2(i, j, '0');}else {//子岛屿dfs2(i, j, '1');}}}}//DFS3:统计岛屿个数int ans = 0;for (i = 1; i <= m; i++) {for (j = 1; j <= n; j++){if (map[i][j] == '1') {ans++;dfs3(i, j);}}}cout << ans<< endl;}return 0;
}这道题连续使用了多次深度优先搜索,很有练习的价值。同时DFS算法由于其递归的性质,失之毫厘差之千里,在小心打代码的同时也要使用尽量简单的逻辑,否则容易出BUG。




)










:搜寻潜水器Problem B: Searching for Submersibles)



