1. 什么是数据结构
数据结构(Data Structure)是计算机存储、组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的集合。
数据结构是用来在内存中管理数据的,类似的,我们熟悉的文件或数据库是在硬盘中管理数据的。内存中的数据是带点存储的,内存大小一般较小(8G/16G),而硬盘中的数据是不带电存储的,大小一般(512G\1T)。带电存储就是用电信号保存数据,如果突然我们的计算机断电了,那内存中的数据就都没了。
带电存储和不带电存储算是相辅相成的关系,内存中的数据处理好了之后,就会存到硬盘上,防止断电后丢失。
2. 算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要用来衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。随着如今硬件的迭代升级,内存越来越大,现在我们已经不太关注空间复杂度了。
3. 时间复杂度
3.1 时间复杂度的概念
在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上讲,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们将每个算法都上机测试运行时间很麻烦,所以才有了时间复杂度这个分析方式。一个算法花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
那么我们现在判断一下下面这段代码的时间复杂度
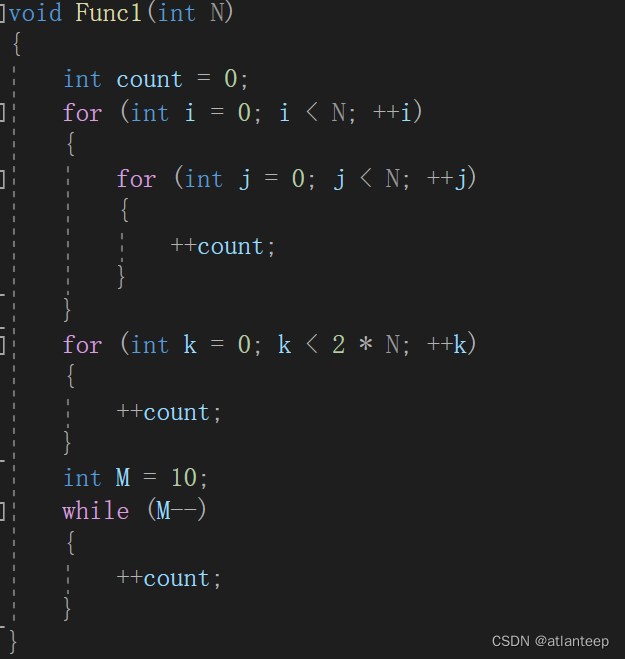
首先是两层循环嵌套:F(N) = N^2
然后是2*N次的循环:F(N) = 2 * N
最后是10次循环:F(N) = 10
把他们都加在一起最终结果就是:F(N) = N^2 + 2*N + 10
但是实际上,我们并不需要把时间复杂度计算的那么精准,只需要知道大概执行次数,所以这里引进了大O的渐进表示法
3.2 大O的渐进表示法
推导大O阶方法:
1. 用常数1替代运行时间中所有加法常数
2. 在修改后的运行次数函数中,只保留最高阶项
3. 如果最高阶项存在且不为1,则去除与这个项相乘的常数
上一道题用大O的渐进表示法的结果就是O(N^2)
其实说白了,这个方法的核心就是去估计最差的预期的数量级有多大
3.3 例题
3.3.1 冒泡排序的时间复杂度

冒泡排序的遍历 (N - 1) + (N - 2) +···+ 3 + 2 + 1 次
很明显这是个等差数列,头加尾除二,最后结果就是 O(N^2)
3.3.2 二分查找的时间复杂度
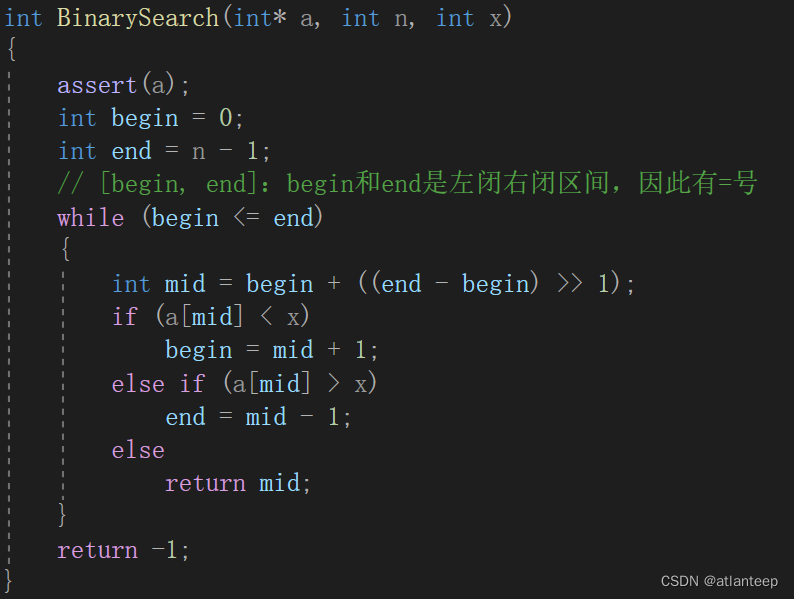
二分查找最开始查找区间长度是N,找一次缩小一半,就是除2,最坏的情况就是最后区间长度缩小为1,或者为-1(没找到)。
那么除多少个2就相当于找了多少次,我们假设除了x个2
N /2 /2 /2······/2 == 1 两边同时成 2^x
N == 2^x
x ==
所以最后二分查找的时间复杂度就是 O(),因为这个对数不好写出来,所以有时候也会简写成 O(logN) ,大家看到这种写法的时候要注意识别。如果不是以2为底的话就不能简写了
3.3.3 计算阶乘的时间复杂度(简单阶乘)

我们分析一下,递出去的时候要走N-1次到头,归回来也要走N-1次,然后最后返回数值走1次,所以说精细算的话一共走2N-1次,时间复杂度为O(N)
4. 空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间的大小的量度。
空间复杂度不是程序占用了多少Byte的空间,而是计算同一时间新开辟变量最多时的新变量个数,如果没有新开辟变量也是是O(1),因为空间是可以重复利用的。
空间复杂度计算规则和时间复杂度类似,也使用大O渐进表示法
其实空间复杂度和时间复杂度的判断都有一种感性的感觉,我们要去思考这个算法的思路是什么,而不是死磕代码里有几个for循环什么的

:搜寻潜水器Problem B: Searching for Submersibles)






)




复习提纲21)

)



