摘要

基于LSTM-Autoencoder模型的多任务空气质量预测
本文提出了一种长短期记忆（LSTM）自编码器多任务学习模型，用于预测城市多个地点的PM2.5时间序列。该模型能够隐式地、自动地挖掘不同站点污染物之间的内在关联性。该模型充分利用了监测站的气象信息，有利于提高模型的性能。

Abstract

文献阅读

题目

Multitask Air-Quality Prediction Based on LSTM-Autoencoder Model

引言

本文提出了一种长短期记忆（LSTM）自编码器多任务学习模型，用于预测城市多个地点的PM2.5时间序列。具体而言，多层LSTM网络可以模拟城市空气污染颗粒物的时空特征，利用堆叠式自动编码器对城市气象系统的关键演变模式进行编码，可为PM2. 5时间序列预测提供重要的辅助信息。此外，多任务学习能够自动发现多个关键污染时间序列之间的动态关系，解决了传统数据驱动方法建模过程中多站点信息利用不足的问题。

创新点

现有的数据驱动方法往往忽略了城市多个站点之间的动态关系，导致预测精度不理想。
文章贡献如下：
1）考虑到空气污染物的复杂时空动态，通过多层LSTM网络的时空学习，探索城市多个位置颗粒物的时空特征。
2）气象因素对PM2.5的演变影响很大。提出了对气象时间序列关键演变模式的编码方法，为PM2. 5时间序列预测提供了重要的辅助信息。
3）PM2.5时间序列的模式在多个地点之间具有很强的相关性，本文利用多任务学习自动探索重点污染监测站之间的模式，并通过深度学习模型隐式地描述各个站点之间的关系。
4）对北京市多站PM2. 5时间序列和气象观测信息的建模仿真表明，由于考虑了多站间的关系，该方法取得了令人满意的性能。

方法

利用长短期记忆网络学习时空演化特征

LSTM网络图：

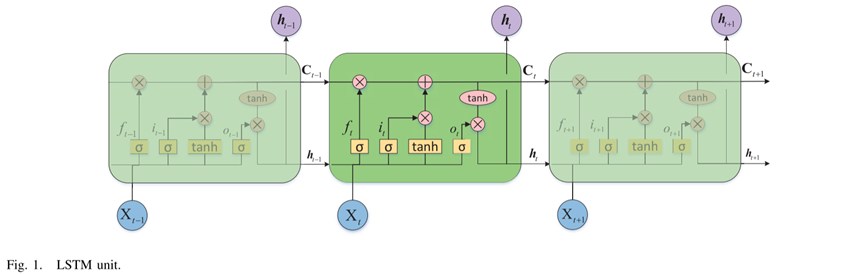
构建用于气象辅助信息编码的堆叠自编码器

1）定义了一个特征学习函数h = fθ (X)，其中fθ(·)称为编码器函数。然后，解码函数X = gθ (h)学习重构原始信号。特征向量h是原始输入的压缩表示。
2）目标是构建气象信息的向量表示，并将其用于PM2.5时间序列的建模。气象自编码器的目标函数可表示为:

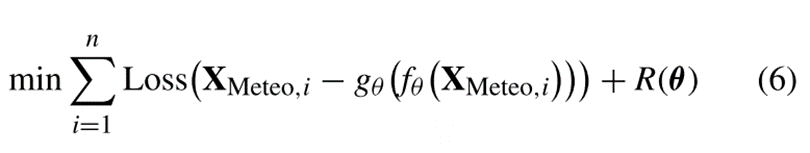
其中：XMeteo,i为第i个监测点位置的气象信息，R(θ)是自编码器权值的约束项。

使用多任务学习发现全市通用模式

1）在硬参数共享中，学习神经网络基础层的公共特征子空间。在基础层中参数是完全相同的，可以防止过拟合问题，有更好的泛化效果。
2）在软参数共享中，任务的模型参数可以是不同的、受规则约束的特征子空间。
3）多任务学习的架构图：

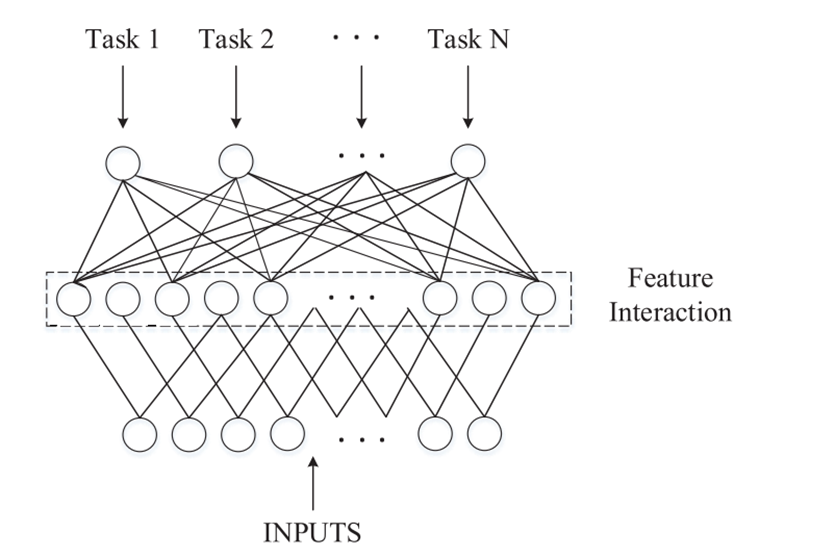
4）多任务学习的目标函数：

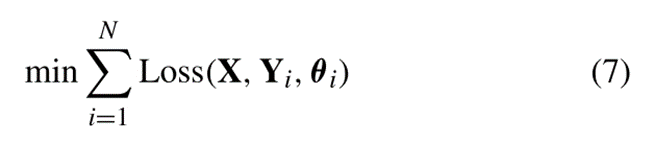
其中：X为多任务输入，Yi为各自的多任务学习目标，θi是第i个任务对应的学习参数，N是任务数。

模型

作者提出的模型的架构如下图所示：

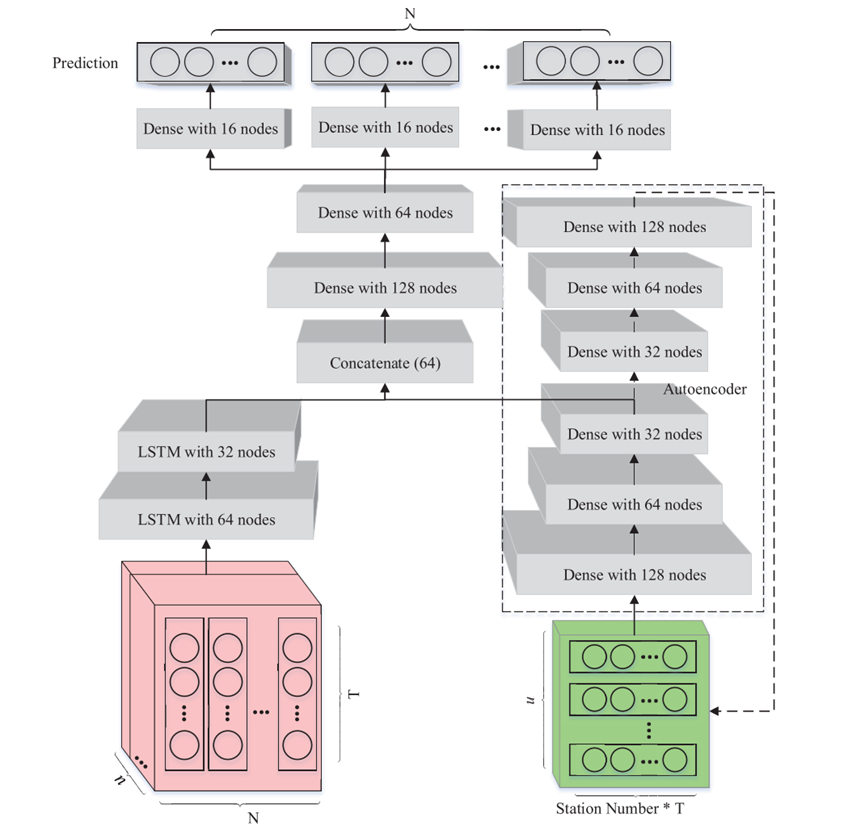
多层LSTM网络对PM2.5时空序列特征进行学习，层叠式自编码器可以逐层压缩有用信息，提高性能。

在更高层次的特征学习上，使用两层密集网络学习PM2.5综合演化信息和气象辅助。基于深度特征，利用多个亚密集层对全市范围内多个地点的PM2.5时间序列进行建模，并输出预测值。整个模型的目标函数为：

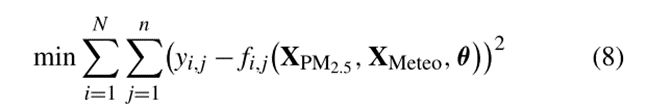
其中：yi,j为PM2.5时间序列实值，N为空气质量监测站的个数，n是时间序列的个数。XPM2.5为所有空气质量监测站的记录值，XMeteo是辅助气象信息的输入，θ为所提模型的所有参数。

实验

数据集

北京的空气质量数据包括几种主要空气污染物的浓度：PM2.5(μg/m3)、PM10(μg/m3)、NO2(μg/m3)、CO(mg/m3)、O3(mg/m3)和SO2(μg/m3)。北京有18个监测站。名称、纬度和经度如下表所示。监测站包括市区、郊区和交通污染监测区。

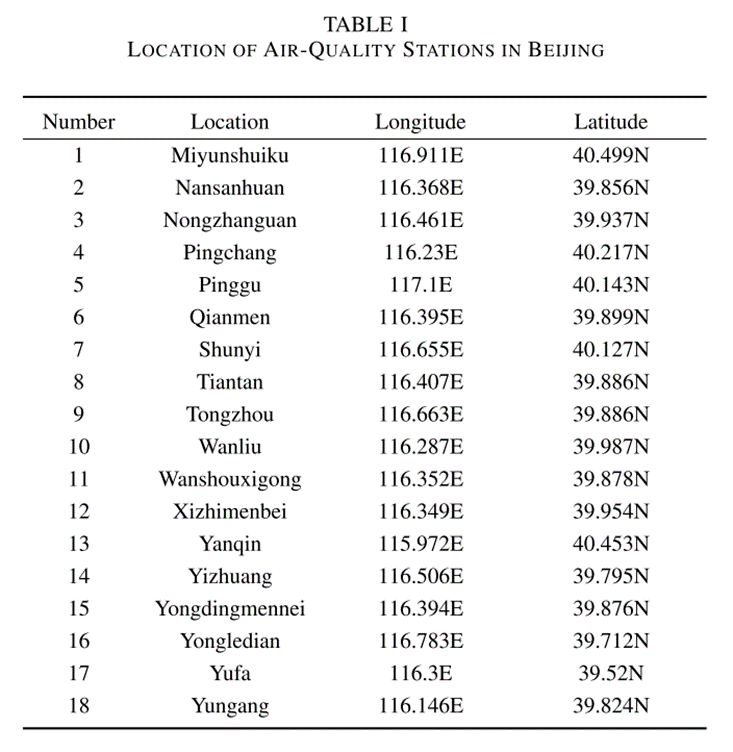
时间序列从2017年1月30日下午4点到2018年1月31日下午3点每小时采样一次，共8784个样本。

利用气象信息作为辅助信息，包括温度、压力、湿度、风向、风速和天气情况。共有13个气象站，位置如下所示：

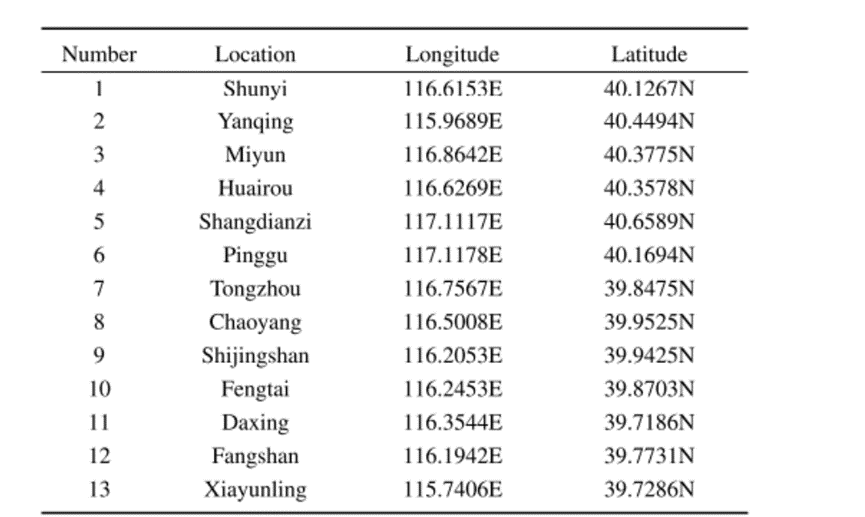
评估准则

优化方法是最常用的ADAM优化器，使用三个评价指标来比较所提出模型的性能：均方根误差(RMSE)、平均绝对误差(MAE)和对称平均绝对百分比误差(SMAPE)。

实验结果

在北京市多个气象监测站的预报结果如下，选取了几个有代表性的气象监测站的预报结果。这些地点包括农村地区、城市中心、工业区和路边。

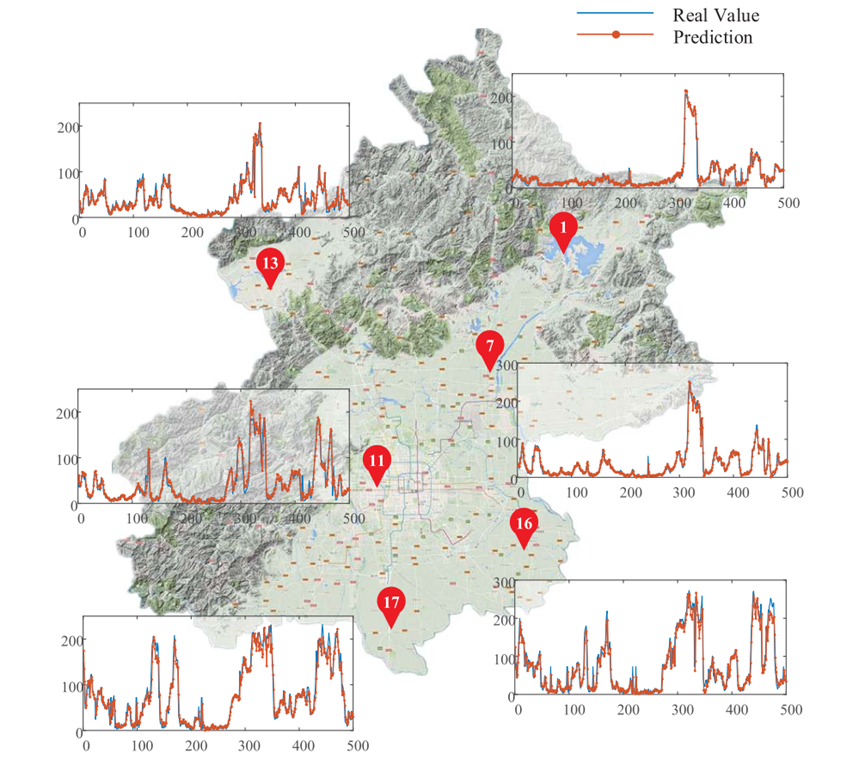
从图中可以看出，多个地点的PM2.5时间序列趋势是一致的，但地点之间在细节上的差异很明显。

该方法对PM2.5时间序列的一步前预测结果和三步前预测结果如下表：

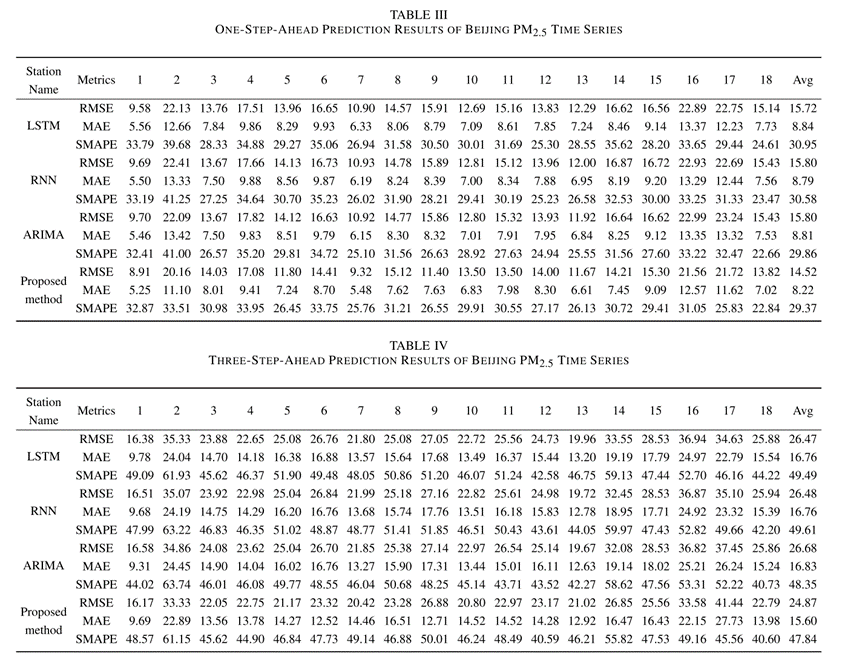
从表中可以看出，提出的方法在各个指标(RMSE、MAE、SMAPE)上都有更好的表现，每个指标的预测误差都比对比方法好10%左右。

LSTM-Autoencoder模型和传统LSTM模型的预测结果对比如下：

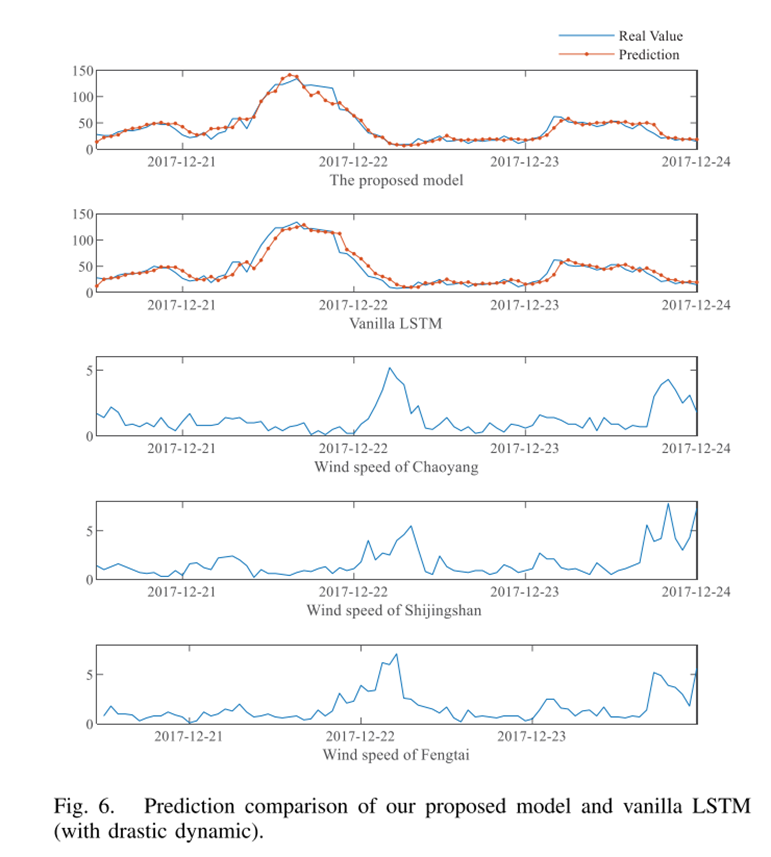
LSTM-Autoencoder模型在12月21日的预测结果优于传统的LSTM模型。预测曲线增长快，能有效地预测空气质量。相比之下，传统LSTM无法跟踪PM2.5时间序列的趋势。两者之间预测结果相差很大.

深度学习

Self-attention

self-Attention由来

Google在2017年发表了著名的论文《Attention Is All You Need》提出了目前在NLP以及CV领域使用非常广泛的transformer模型，而self-attention是transformer的主要组成部分。

在transformer之前，NLP领域常见的处理序列数据的方法主要是RNN/LSTM等：

A：由于RNN/LSTM在计算时需考虑前序信息，所以不能并行，导致训练时间较长

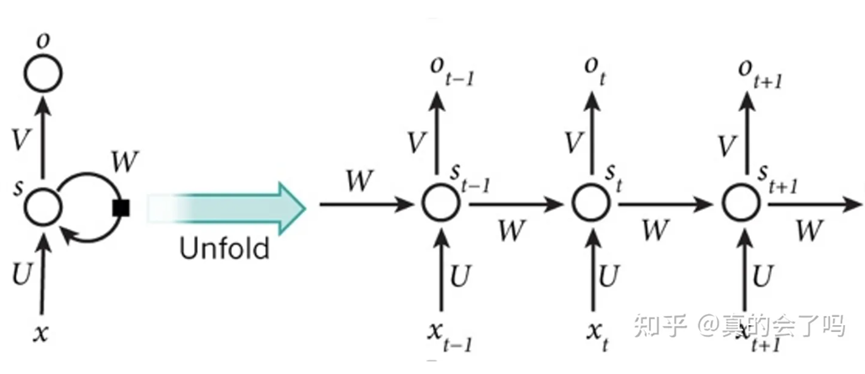
B：当序列长度过长时，由于模型深度增加，序列开始部分对末端部分影响几乎会消失，虽然记忆网络/attention机制的加入可以降低一部分影响，但长距依赖问题仍然存在。

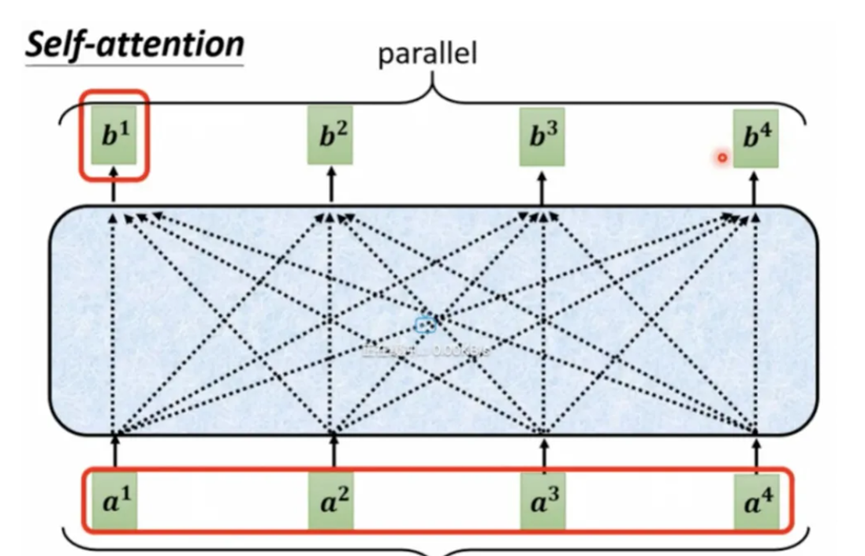
Self-attention可以很好的处理上面两个问题，首先，self-attention通过位置编码保证序列关系，计算上不依赖序列关系，所以可以实现完全的并行，其次，在计算相关性时候，任何一个点都会与整个序列中的所有输入做相关性计算，避免了长距依赖的问题。

self-attention原理

从输入和输出的不同形式来看，经典的NLP任务可以分为下面三种情况：
A：输出和输出长度一致，典型任务：词性识别

B：输入和输出长度不一致，输出长度不变并且输出为单一元素，典型任务，文本分类，情绪识别

C：输入和输出长度不一致，并且输出输出长度不定，为多个长度不固定的元素，典型任务：翻译，文本摘要等

从上面的任务形式可以看出，无论是那种任务，我们既想让模型知道不同输入向量之间的关系以及单个输入向量与和整体输入之间的关系，同时也想让模型了解不同的输入对输出的贡献是怎么样的，Self-attention可以完成上面两个部分的任务，下面我们看是如何做到的：

A：不同输入之间相关性计算
度量两个向量的相关性的方法有很多，点乘是常用的方法之一。在self-attention中就是用这种方法来做不同输入向量之间的相关性计算，每个单词通过与Wq做乘法后，作为当前单词的表征，为查询向量Query，每个单词通过与Wk做乘法后，当作被查询向量Key，最后每个输入向量的Query与其他输入向量的Key做点乘，来表征两个不同向量的相关性。

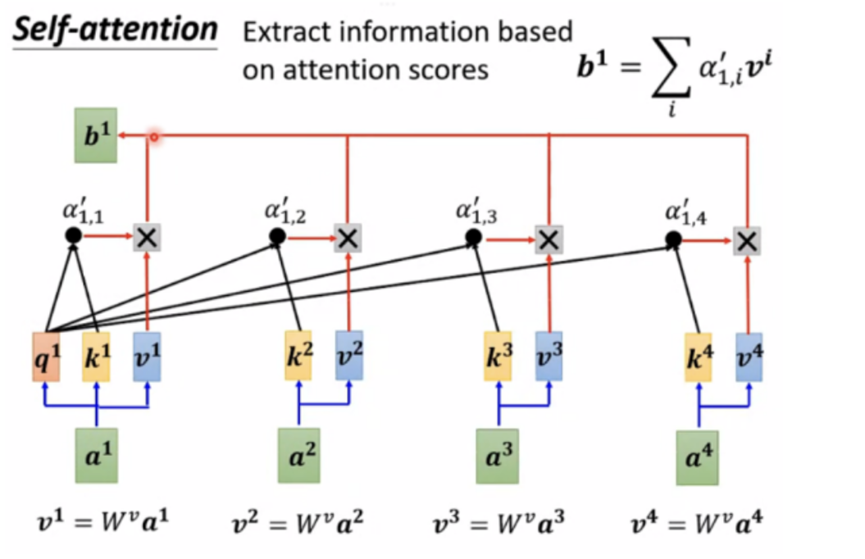
B：信息提取
将每个输入与Wv相乘，生成V，将当前输入的alpha与每个输入的V相乘，在相加就得到了完成了输入的有用信息抽取，这里输出的b1的数值是和最大的alpha*v的值是接近的，也就是突出了贡献比较大的输入。依此类推，可以同时计算b1…到bn，这样整体上一个self attention的大部分计算就完成了，b1，b2….到bn都是可以并行计算的。

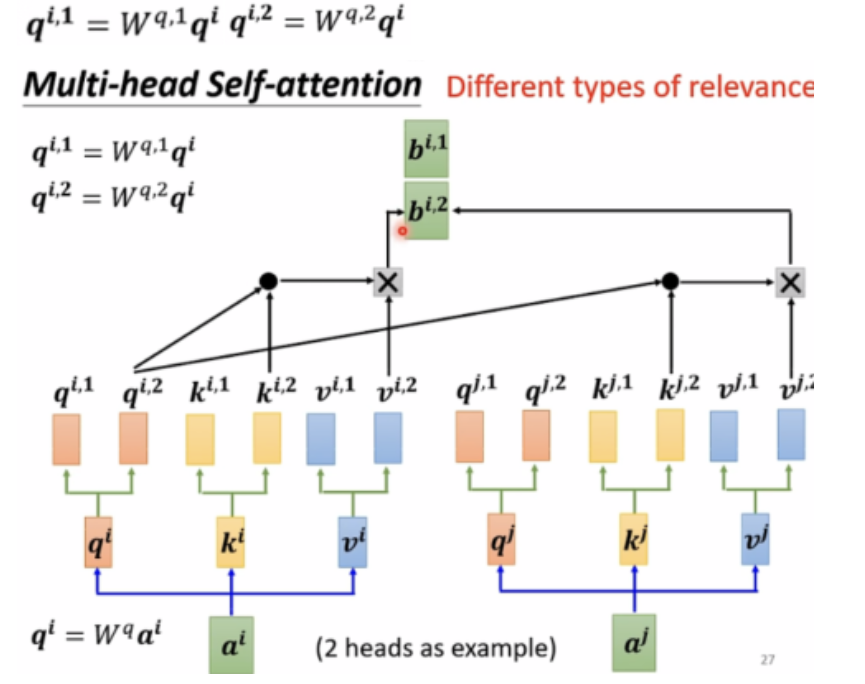
C：Multi-head attention
在实际使用过程中，一个attention很难关注到所有信息，所以基本上都是使用Multi-head attention，也就是说每个输入向量有多个Q，多个K，多个V，每一个组内的q只和自己组内的k，v做计算，如下图中画红色框的元素所示：

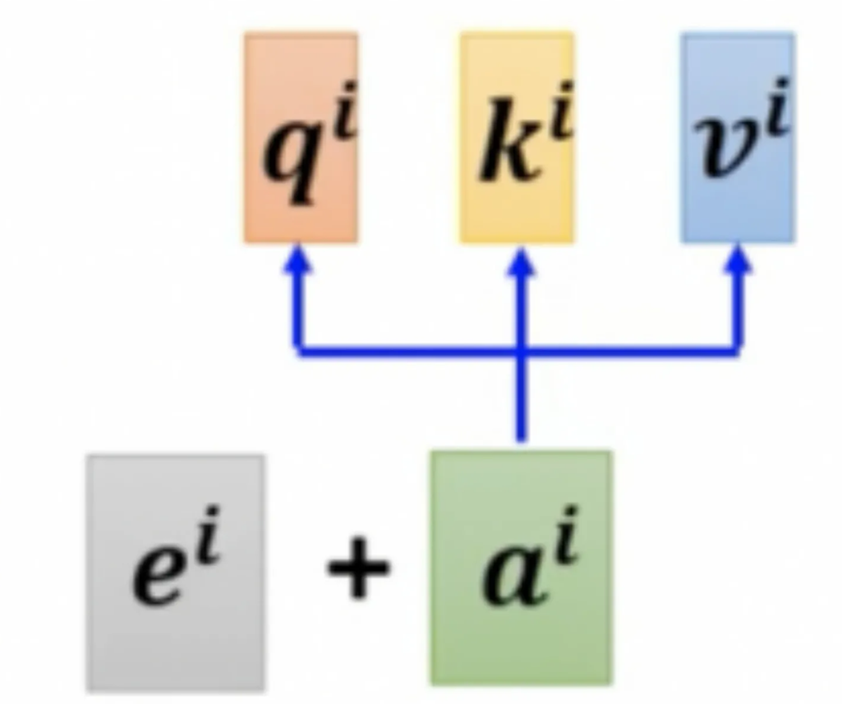
D：输入-位置编码
Self attention本身是不涉及到位置信息的，但是在输入层已经将位置信息加入进来了，这块有比较重要，所以单独放在这里了。对于大部分任务位置信息是很重要的信息，比如词性标注中，动词和名词的关系，所以我们会在输入中加入特殊形式的位置编码，我理解位置编码只要保证唯一性和相对关系就是可以的，至于不同位置编码的效果还是以实验效果为准。

self attention代码

论文中关于attention的公示描述：

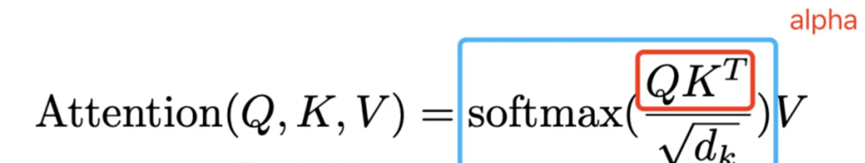
可以将公式和下面的图联系在一起：

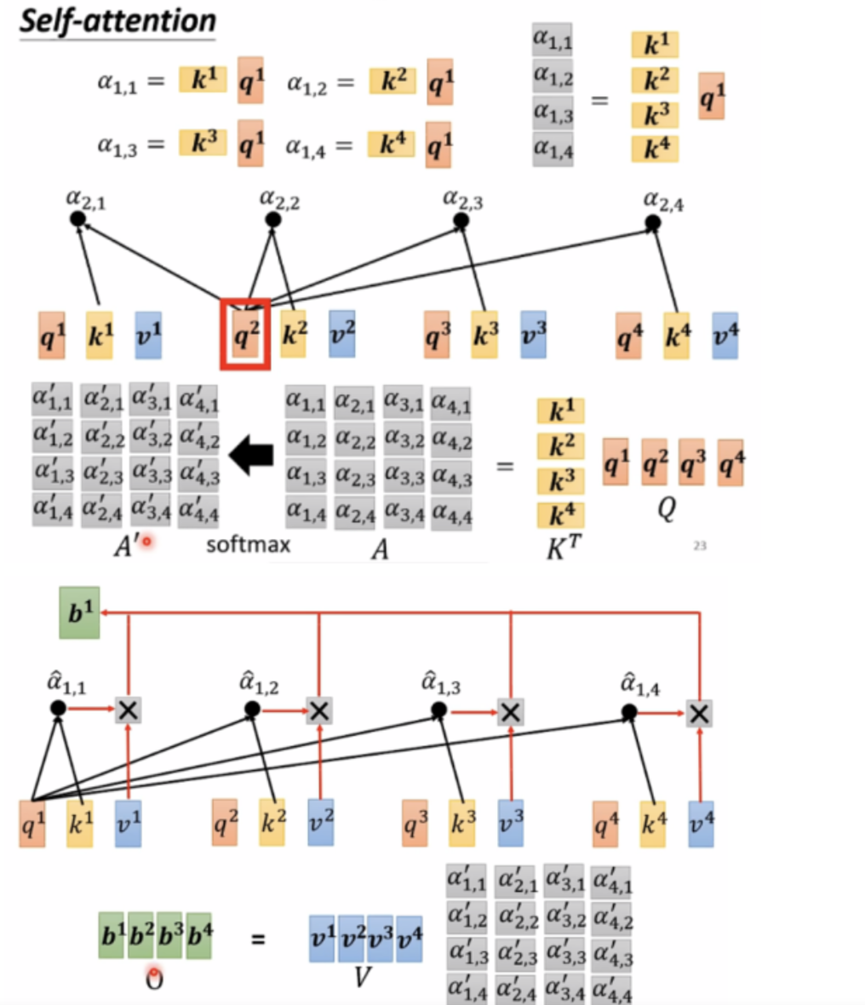
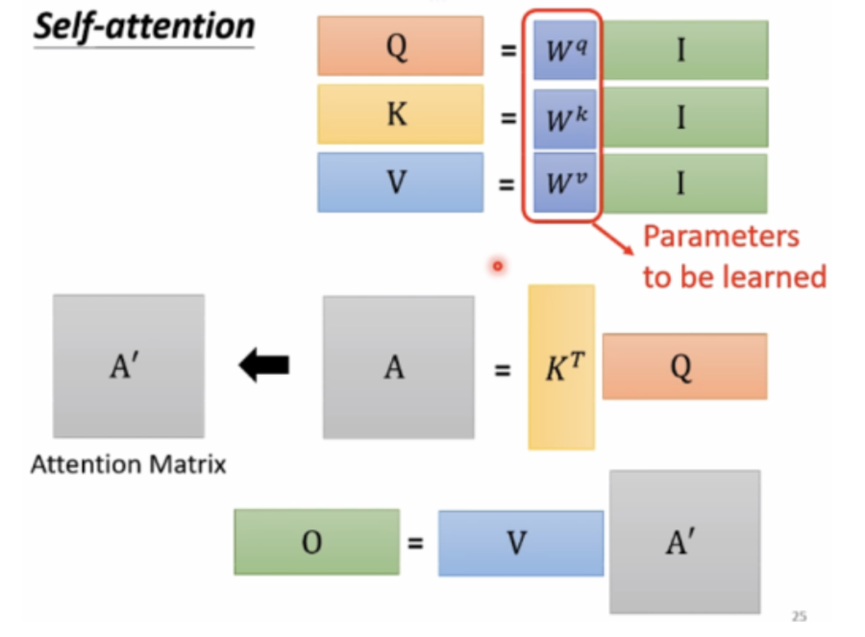
上图是Attention公式的实现步骤，从图中可以看出 ，一个attention模块，需要学习的参数只有Wq，Wk，Wv这三个投影矩阵。

首先我们看init函数，self.num_attention_heads是multi-head中head的个数，self.attention_head_size每个attention的头维度，self.all_head_size和config.hidden_size是一样的值，Q，K，V的计算主要是矩阵相乘。

class BertSelfAttention(nn.Module):def __init__(self, config):super(BertSelfAttention, self).__init__()   # 768 12if config.hidden_size % config.num_attention_heads != 0:raise ValueError("The hidden size (%d) is not a multiple of the number of attention ""heads (%d)" % (config.hidden_size, config.num_attention_heads))self.num_attention_heads = config.num_attention_headsself.attention_head_size = int(config.hidden_size / caonfig.num_attention_heads)self.all_head_size = self.num_attention_heads * self.attention_head_size#计算Q，K，V self.query = nn.Linear(config.hidden_size, self.all_head_size)self.key = nn.Linear(config.hidden_size, self.all_head_size)self.value = nn.Linear(config.hidden_size, self.all_head_size)self.dropout = nn.Dropout(config.attention_probs_dropout_prob)

transpose_for_scores的计算主要是将矩阵的维度做转换[bs ，seqlen ， all_head_size ]转换成[bs， num_ head ，seqlength，attention_head_size ]，为了后续multi-head 做attention计算。

 def transpose_for_scores(self, x):new_x_shape = x.size()[:-1] + (self.num_attention_heads, self.attention_head_size)x = x.view(*new_x_shape)return x.permute(0, 2, 1, 3)

forward是代码的主要流程部分：

# input matrix是[bs, seqlength, hidden_size]def forward(self, hidden_states, attention_mask):mixed_query_layer = self.query(hidden_states)mixed_key_layer = self.key(hidden_states)mixed_value_layer = self.value(hidden_states)# 计算Q，K，V之后大小不变query_layer = self.transpose_for_scores(mixed_query_layer)key_layer = self.transpose_for_scores(mixed_key_layer)value_layer = self.transpose_for_scores(mixed_value_layer)#query_layer，key_layer，value_layer，大小变为  [bs, num_ head  , seqlength, attention_head_size]# Take the dot product between "query" and "key" to get the raw attention scores.# alpha矩阵 的计算以及单位化 Q*transpose(K)attention_scores = torch.matmul(query_layer, key_layer.transpose(-1, -2))attention_scores = attention_scores / math.sqrt(self.attention_head_size)# Apply the attention mask is (precomputed for all layers in BertModel forward() function)# 每一条输入，padding部分不做计算，所以要进行mask，# attention_mask在transformer中有不同的作用，详细信息见参考文件attention_scores = attention_scores + attention_mask# Normalize the attention scores to probabilities.# alpha矩阵归一化attention_probs = nn.Softmax(dim=-1)(attention_scores)# This is actually dropping out entire tokens to attend to, which might# seem a bit unusual, but is taken from the original Transformer paper.attention_probs = self.dropout(attention_probs)# 计算softmax（alpha） * V# 将矩阵维度变换到之前，属于与输出维度保持不变context_layer = torch.matmul(attention_probs, value_layer)context_layer = context_layer.permute(0, 2, 1, 3).contiguous()new_context_layer_shape = context_layer.size()[:-2] + (self.all_head_size,)context_layer = context_layer.view(*new_context_layer_shape)return context_layer

从整体上看，self-attention的输入输出维度一致，输入之前不仅加入了位置编码，还需要将不同作用的部分需要的mask（例如padding等，防止模型作弊）加入进来。

总结