球和球面是数学和物理学中非常重要的概念，它们在许多领域都有广泛的应用。
球面是指所有与固定点等距离的点的集合，这个固定点被称为球心，而这个等距离的长度就是球的半径。球面是一个二维曲面，它是三维空间中点与距离之间关系的数学表示。球面在几何学、天文学、工程学等领域都有广泛的应用。
球是指所有与固定中心点等距离的点的集合。与球面不同的是，球是一个三维实体，它可以被看作是一个连续的点集。球在数学、物理学、工程学等领域都有广泛的应用，例如在计算球的体积、表面积、球的转动惯量等方面都有重要的应用。
在三维空间、欧几里得、几何学，球面被设定为是在R空间中与一个定点距离为r的所有点的集合，此处r是一个正的实数，称为半径，固定的点称为球心或中心，并且不属于球面的范围。r = 1是球的特例，称为单位球。
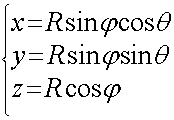
球和球面有一些重要的性质和特点。首先，球的表面积公式是 4πr^2，其中 r 是球的半径。这个公式是通过微积分的方法推导出来的，它表示球的表面积与其半径之间的关系。其次，球的体积公式是 4/3πr^3，这个公式表示球的体积与其半径之间的关系。此外，球面还具有一些几何性质，例如它的曲率是常数，等于该点到球心的距离的倒数。
最后，球和球面在现实生活中被广泛应用。首先，在天文学中，星球的表面可以被近似地看作是一个球面或球体，因此球和球面的理论在天文学中有广泛的应用。其次，在物理学中，许多物理现象可以通过球和球面的理论来描述，例如球的转动惯量、球的弹性碰撞等。此外，在工程学中，球和球面的理论也被广泛应用于建筑设计、机械工程和电子工程等领域。
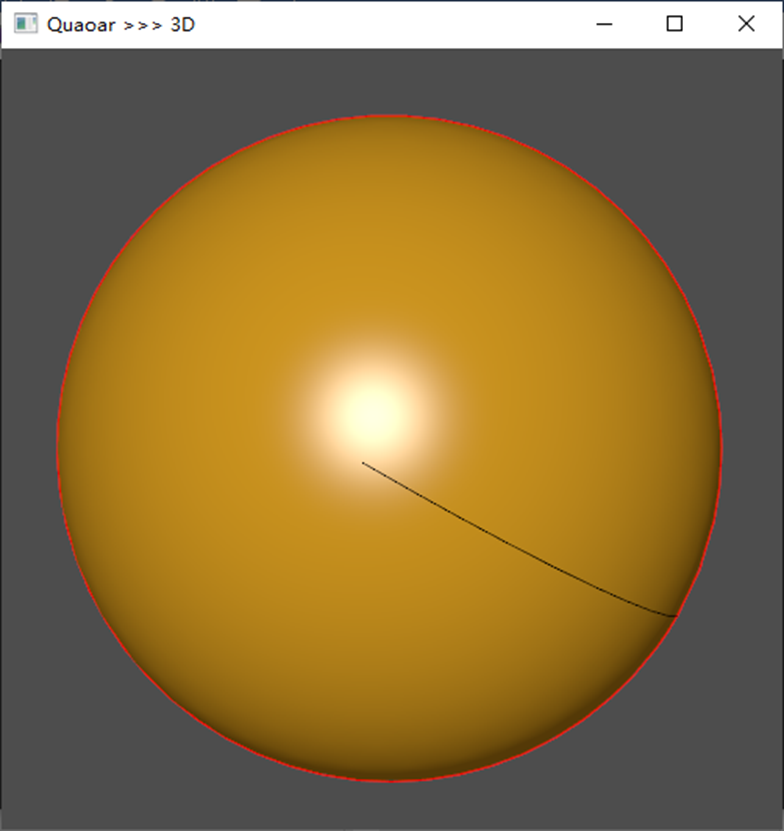
下面基于OCC计算球面上曲线的长度：
先生成球面上曲线的离散点，再把这些离散点拟合曲线，最后计算该曲线的长度。
所计算曲线实际上为球面上的最大圆。
#include <Geom_SphericalSurface.hxx>
#include <GeomAPI_Interpolate.hxx>
#include <BRepAdaptor_Curve.hxx>
#include <BRepBuilderAPI_MakeEdge.hxx>
#include <GCPnts_AbscissaPoint.hxx>
#include <BRepPrimAPI_MakeSphere.hxx>
#include "Viewer.h"
int main(int argc, char* argv[])
{TColgp_HArray1OfPnt Points(1, 21);
Standard_Real u0 = 0.0;Standard_Real u1 = 2*M_PI;Standard_Real v0 = -M_PI_2;Standard_Real v1 = M_PI_2;Handle(Geom_SphericalSurface) aSphere=new Geom_SphericalSurface(gp_Ax3(), 30.0);BRepPrimAPI_MakeSphere mkSphere(30.0);TopoDS_Shape Sphere = mkSphere.Shape();double uInter = (u1 - u0)/20;double vInter = v1 - v0;//生成点for (int i = 0; i < 21; i++) {Points[i + 1] = aSphere->Value(i * uInter, 0.0);}//曲线拟合GeomAPI_Interpolate Interp(&Points, Standard_False, Precision::Confusion());Interp.Perform();Standard_Boolean isFin = Interp.IsDone();Handle(Geom_BSplineCurve) aBsCurve = Interp.Curve();TopoDS_Edge aE = BRepBuilderAPI_MakeEdge(aBsCurve);//计算长度BRepAdaptor_Curve aDapC(aE);double length = GCPnts_AbscissaPoint::Length(aDapC);std::cout << "OCC计算的长度：" << length << std::endl;Viewer vout(50, 50, 500, 500);vout << aE;vout << Sphere;vout.StartMessageLoop();return 0;
}
OCC计算的长度：188.497
理论长度为：60*π
计算长度与理论长度十分接近。
