本篇目标了解,翻转数组的经典解法,
189. 轮转数组 - 力扣(LeetCode)
目录
基本方法概述:
1,翻转做法,推荐时O(n),空(1)
2,环状替换,极不推荐(思路好像,但官方的解释比较难理解,官方题解更像是在秀操作,)时O(n)空(1)
3,创建临时数组,拷贝完后,再拷贝回去,时O(n),空O(n);显现不出自身水平,尤其在掌握了翻转做法,这就太过时了
4,单个临时变量,来一遍一遍的循环重复,向右轮转的操作(如果K和数组本身较大,时间耗损的多),时O(n^2),空(1)太LOW了
翻转法的代码:

基本方法概述:
1,翻转做法,推荐时O(n),空(1)
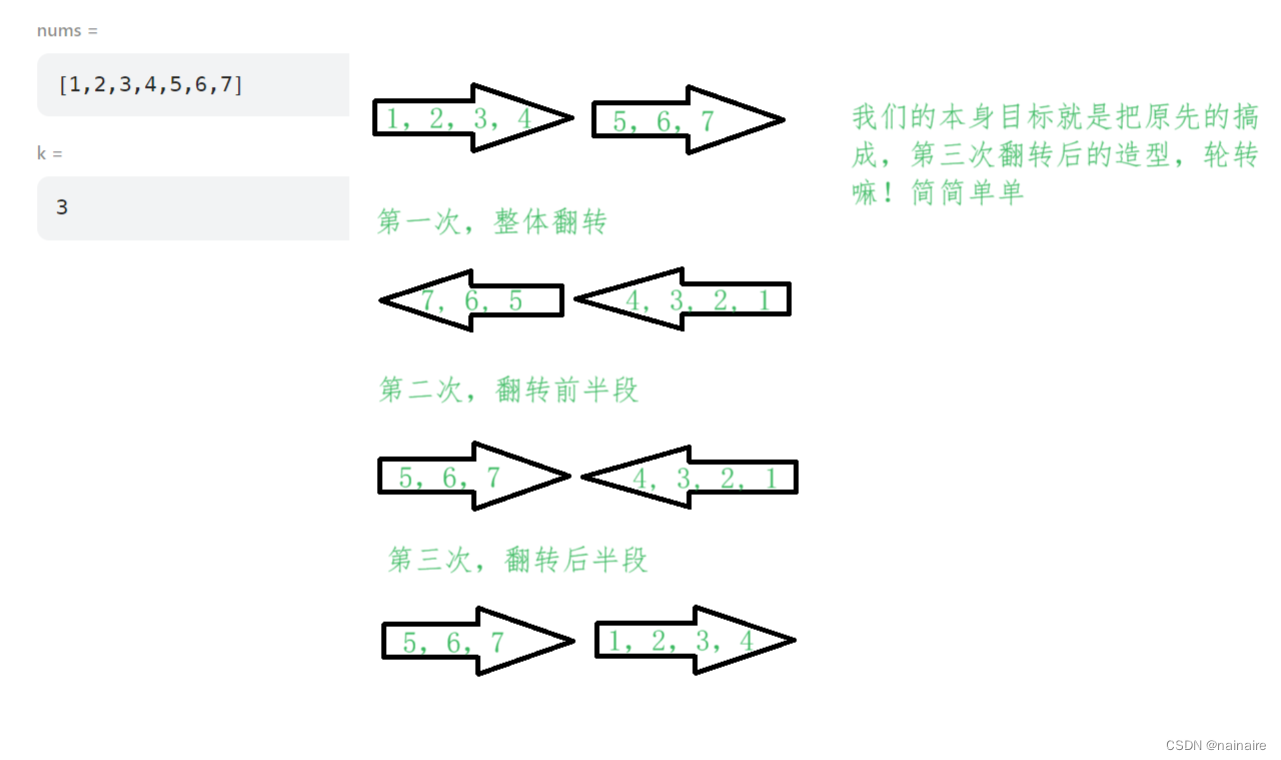
2,环状替换,极不推荐(思路好像,但官方的解释比较难理解,官方题解更像是在秀操作,)时O(n)空(1)
环状替换的思路,主要思想是:一次性(一步到位,而且不会),排到,轮转k次的位置,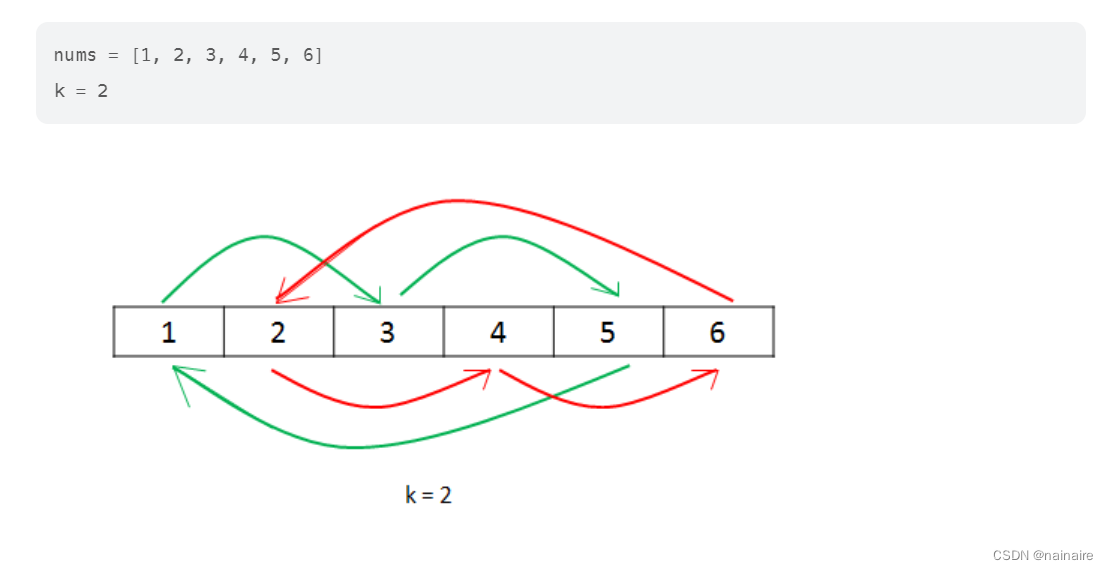
3,创建临时数组,拷贝完后,再拷贝回去,时O(n),空O(n);显现不出自身水平,尤其在掌握了翻转做法,这就太过时了
4,单个临时变量,来一遍一遍的循环重复,向右轮转的操作(如果K和数组本身较大,时间耗损的多),时O(n^2),空(1)太LOW了
翻转法的代码:
void rotate(int* nums, int numsSize, int k) {k = k % numsSize;//轮转numsSize*n+k次和轮转k次没有区别int tmp = 0;//数组翻转法,可以用函数来分装翻转的操作,会清晰一些,不过这里就没这么做了for(int i = 0; i < numsSize / 2; ++i){//翻转alltmp = nums[i];nums[i] = nums[numsSize - i - 1];nums[numsSize - i - 1] = tmp;}for(int i = 0; i < k / 2; ++i){//翻转前半段tmp = nums[i];nums[i] = nums[k - i - 1];nums[k - i - 1] = tmp;}for(int i = 0; i < (numsSize - k) / 2; ++i){//翻转后半段tmp = nums[k + i];nums[k + i] = nums[numsSize - 1 - i];nums[numsSize - 1 - i] = tmp;}
}
每日一表情包:



:linux安装 黑方容灾备份与恢复系统软件v6.0 代理)
传输 CAN 和 FlexRay 帧)


)
 执行 SQL 用法)








】树、二叉树详解)


