地毯填补问题
题目描述
相传在一个古老的阿拉伯国家里,有一座宫殿。宫殿里有个四四方方的格子迷宫,国王选择驸马的方法非常特殊,也非常简单:公主就站在其中一个方格子上,只要谁能用地毯将除公主站立的地方外的所有地方盖上,美丽漂亮聪慧的公主就是他的人了。公主这一个方格不能用地毯盖住,毯子的形状有所规定,只能有四种选择(如图):

并且每一方格只能用一层地毯,迷宫的大小为 2 k × 2 k 2^k\times 2^k 2k×2k 的方形。当然,也不能让公主无限制的在那儿等,对吧?由于你使用的是计算机,所以实现时间为 1 1 1 秒。
输入格式
输入文件共 2 2 2 行。
第一行一个整数 k k k,即给定被填补迷宫的大小为 2 k × 2 k 2^k\times 2^k 2k×2k( 0 < k ≤ 10 0\lt k\leq 10 0<k≤10);
第二行两个整数 x , y x,y x,y,即给出公主所在方格的坐标( x x x 为行坐标, y y y 为列坐标), x x x 和 y y y 之间有一个空格隔开。
输出格式
将迷宫填补完整的方案:每一补(行)为 x y c x\ y\ c x y c( x , y x,y x,y 为毯子拐角的行坐标和列坐标, c c c 为使用毯子的形状,具体见上面的图 1 1 1,毯子形状分别用 1 , 2 , 3 , 4 1,2,3,4 1,2,3,4 表示, x , y , c x,y,c x,y,c 之间用一个空格隔开)。
样例 #1
样例输入 #1
3
3 3
样例输出 #1
5 5 1
2 2 4
1 1 4
1 4 3
4 1 2
4 4 1
2 7 3
1 5 4
1 8 3
3 6 3
4 8 1
7 2 2
5 1 4
6 3 2
8 1 2
8 4 1
7 7 1
6 6 1
5 8 3
8 5 2
8 8 1
提示
spj 报错代码解释:
- c c c 越界;
- x , y x,y x,y 越界;
- ( x , y ) (x,y) (x,y) 位置已被覆盖;
- ( x , y ) (x,y) (x,y) 位置从未被覆盖。
upd 2023.8.19 \text{upd 2023.8.19} upd 2023.8.19:增加样例解释。
样例解释
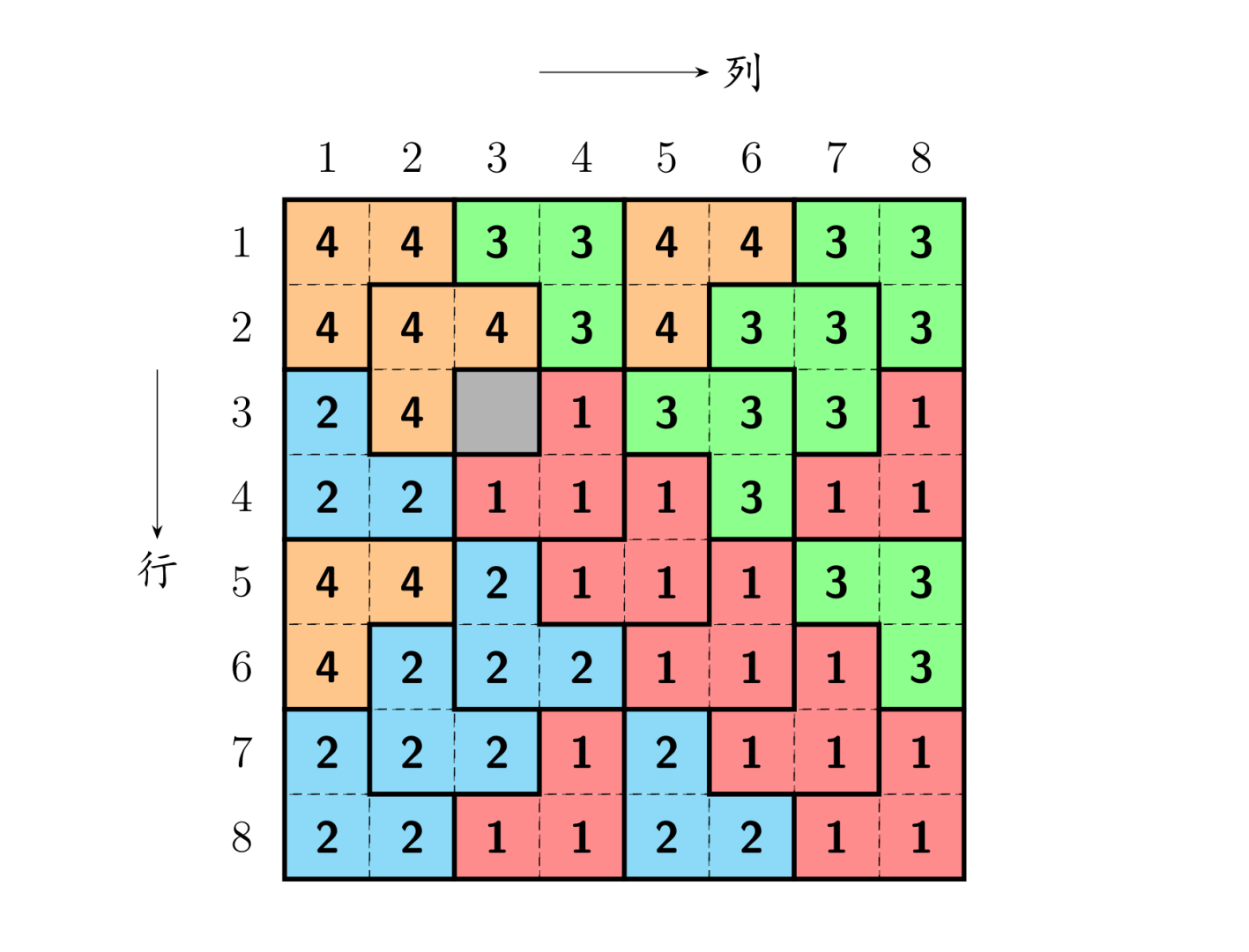
详解
直接dfs过于恐怖,所以经思考后选择分治:
可以每次操作在分成四份的方格中进行
将填充后的格子视为新的“公主”
判断“公主”所在方位,将中间的格子填充好
最后将问题化为子问题——44格子中的简单问题
过程rt
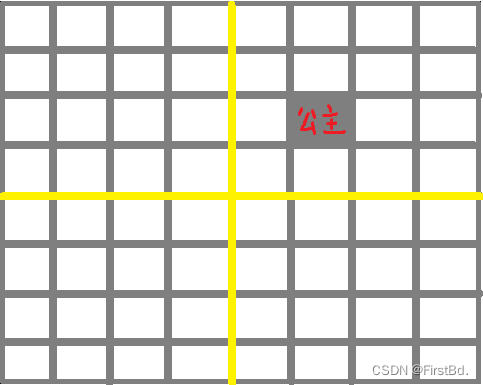
因为公主位于右上角
所以在中间放缺口朝右上角的地毯

再处理右上角
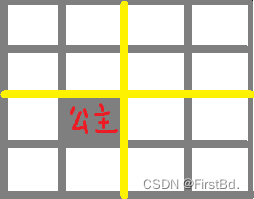
再一次划分时就出现了44的子问题

ACcode
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define mv(x) (1<<(x))
void solve(int x,int y,int a,int b,int l)//递归分治
{if(l==1) return;if(x-a<=l/2-1&&y-b<=l/2-1)//左上{cout<<a+l/2<<" "<<b+l/2<<endl;solve(x,y,a,b,l/2);solve(a+l/2-1,b+l/2,a,b+l/2,l/2);solve(a+l/2,b+l/2-1,a+l/2,b,l/2);solve(a+l/2,b+l/2,a+l/2,b+l/2,l/2);}else if(x-a<=l/2-1&&y-b>l/2-1)//右上{cout<<a+l/2<<" "<<b+l/2-1<<endl;solve(a+l/2-1,b+l/2-1,a,b,l/2);solve(x,y,a,b+l/2,l/2);solve(a+l/2,b+l/2-1,a+l/2,b,l/2);solve(a+l/2,b+l/2,a+l/2,b+l/2,l/2);}else if(x-a>l/2-1&&y-b<=l/2-1)//左下{cout<<a+l/2-1<<" "<<b+l/2<<endl;solve(a+l/2-1,b+l/2-1,a,b,l/2);solve(a+l/2-1,b+l/2,a,b+l/2,l/2);solve(x,y,a+l/2,b,l/2);solve(a+l/2,b+l/2,a+l/2,b+l/2,l/2);}else//右下{cout<<a+l/2-1<<" "<<b+l/2-1<<endl;solve(a+l/2-1,b+l/2-1,a,b,l/2);solve(a+l/2-1,b+l/2,a,b+l/2,l/2);solve(a+l/2,b+l/2-1,a+l/2,b,l/2);solve(x,y,a+l/2,b+l/2,l/2);}
}
signed main()
{cin>>k>>x>>y;len=mv(k);solve(x,y,1,1,len);return 0;
}



)





)



)





