目录
搜索二叉树的相关概念和性质
搜索二叉树的查找
搜索二叉树的插入
搜索二叉树的删除
1.删除节点只有右子树，左子树为空
2.删除节点只有左子树，右子树为空
3.删除节点左右子树都不为空
搜索二叉树的完整代码实现
搜索二叉树的相关概念和性质
搜索二叉树（Binary Search Tree，简称BST）是一种树形数据结构，具有以下性质：
- 每个节点最多有两个子节点，分别称为左子节点和右子节点
- 左子节点的值小于父节点的值，右子节点的值大于父节点的值
- 中序遍历搜索二叉树得到的序列是有序的
搜索二叉树提供了快速的插入、删除和搜索操作，因为它能够通过比较节点值来减少搜索的范围。比如，要搜索一个值为x的节点，可以从根节点开始，如果x小于当前节点的值，则继续在左子树中搜索，如果x大于当前节点的值，则继续在右子树中搜索。重复这个过程，直到找到目标节点或者搜索到叶子节点。
插入和删除操作同样也是通过比较节点值来找到合适的位置进行操作的。具体的插入和删除操作可以根据需要进行扩展，保持BST的特性。
BST的时间复杂度取决于树的高度，在最坏情况下（树被构造成链表），时间复杂度为O(n)，其中n是节点的数量。但是在平均情况下，BST的时间复杂度是O(log n)。
搜索二叉树的应用非常广泛，比如数据库索引、缓存等。它提供了高效的数据访问操作，并且能够保持数据的有序性。
如下图就是一颗搜索二叉树，如果我们对这颗搜索二叉树进行遍历的话，我们就会得到 0 1 2 3 4 5 6 7 8 9 的有序队列，也就是我们上述提到的第三条性质。
我们随便拿到其中的一部分进行说明，对于任意一个节点他的左子节点一定小于该节点，而该节点一定小于该节点的右子节点
搜索二叉树的查找
搜索二叉树一般有三种操作：查找，插入，删除
而在其中查找是最为容易的，同时其他俩个操作也都是基于查找实现的。对于一颗搜索二叉树，因为他的规则是否的明确，节点之间是存在明确的大小关系的，所以我们就利用这个大小关系来进行查找操作，具体操作起来有点像二分查找，我们首先拿要查找的值与根节点的值进行比较，如果根节点的值就是我们要查找的元素，那我们就查找成功，然后返回。如果根节点的值<查找的值，那就说明我们要查找的值在根节点的右子树，如果根节点的值>查找的值，那就说明我们要查找的值在根节点的左侧。然后我们反复的将左右子树的根节点带入进行判断。最终我们就可以得出结果。
我们给出如下的图示举例：
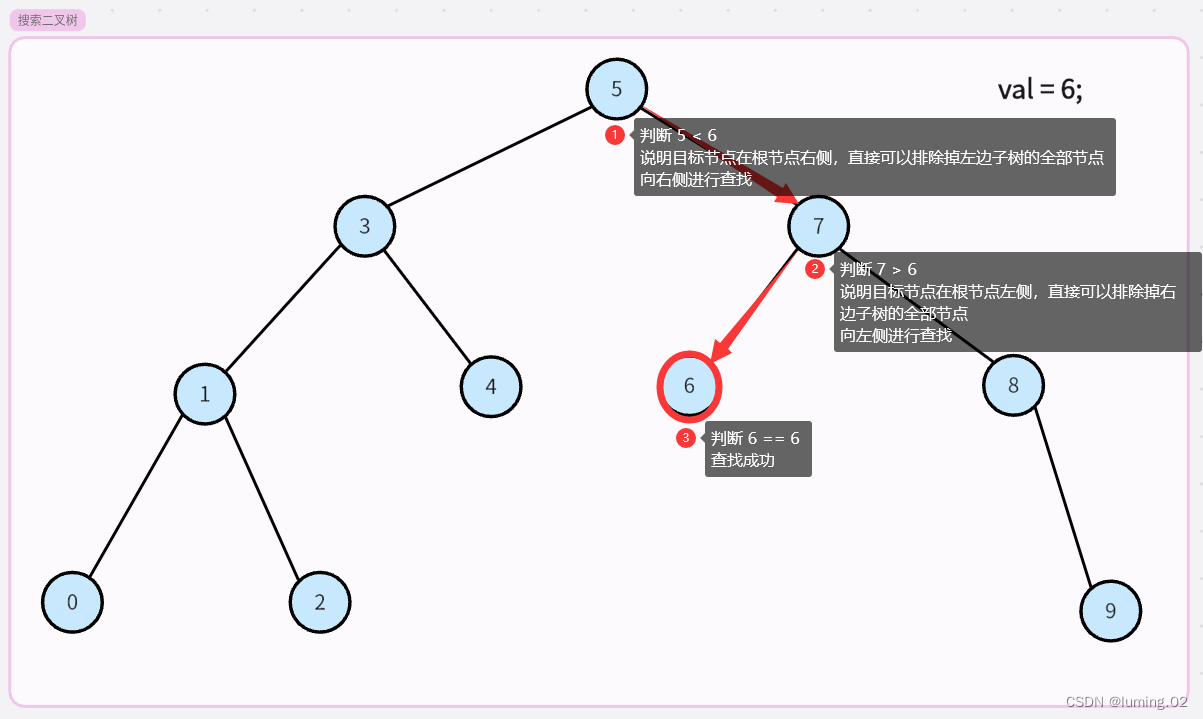
对于这样的搜索过程，我们可以分析他的效率，第一次查找我们排除了左边5个节点，第二次查找我们排除了右边2个节点，我们仅仅进行了3次判断就得到了我们想要的结果。这相较于我们常规的数组二分查找，提高了效率和确定性。由此可见搜索二叉树的效率还是非常高的。
对于这样的搜索过程，我们可以给出相应的代码：
//查找public boolean search(int val) {TreeNode cur = root;while (cur != null) {if (cur.val == val) {return true;} else if (cur.val < val) {cur = cur.right;} else {cur = cur.left;}}return false;}搜索二叉树的插入
对于搜索二叉树的插入，我们需要解决俩个问题：
- 找到往哪个节点后插入
- 往这个节点后插入时选择左子节点还是右子节点
对于第一个问题，其实本质上就是对节点的查找，查找出合适的插入节点；对于第二个问题，我们需要判断插入节点和目标节点的值的大小关系，另外在代码层面实现时有一点需要注意，我们找到插入节点的位置后，在使用指针指向的时候要避免空指针的问题，我们用下图举例：
假如我们要将节点 “7” 插入到搜索二叉树中，原本节点 “6” 的左右子节点都为空，那我们在插入的时候就不能直接将新节点的值赋给这俩个空节点，不然就会出现 null = newNode 这样的空指针异常，所以我们必须要将插入节点的父节点记录下来，通过父节点的指向来进行插入
//插入public void insert(int val) {TreeNode newNode = new TreeNode(val);if (root == null) {root = newNode;return;}TreeNode cur = root;//记录插入节点TreeNode parent = null;//插入节点的父亲节点while (cur != null) {if (cur.val < val) {parent = cur;cur = cur.right;} else if (cur.val > val) {parent = cur;cur = cur.left;}else {//重复元素不予插入return;}}//判断在父亲节点的左边还是右边进行插入if (parent.val < val) {parent.right = newNode;} else {parent.left = newNode;}}搜索二叉树的删除
对于整个搜索二叉树的操作中，删除节点是最麻烦的，因为我们需要对很多种情况进行判断
因为BST中元素与元素之间是存在严谨的大小关系的，所以在我们删除元素之后也应该任然保持这样的关系，为此我们将删除节点可能出现的情况做出分类：
- 删除节点只有右子树，左子树为空
- 删除节点只有左子树，右子树为空
- 删除节点左右子树都不为空
尽管我们对删除节点的状态做出了分类，但这任然不能包含所有的情况，上述三种情况是对删除节点的子树情况做出的分类，事实上删除节点的位置，也就是和父节点的关系也会影响我们的删除过程。以下我们分别对上述三种情况做出进一步的分类：
1.删除节点只有右子树，左子树为空
如图，在这种情况下，我们根据删除节点的位置又可以分出三类：
情况一：当删除节点为根节点的时候，因为删除节点没有左子树，所以我们直接将删除节点的右子节点更新为新的根节点，也就是
root = cur.right;情况二：当删除节点为父亲节点的左子节点的时候，因为删除节点没有左子树，所以我们直接让父亲节点的左指针指向删除节点的右子节点，也就是
parent.left = cur.right;情况三：当删除节点为父亲节点的右子节点的时候，因为删除节点没有左子树，所以我们直接让父亲节点的右指针指向删除节点的右子节点，也就是
parent.right = cur.right;以上便是删除节点左子树为空的情况
2.删除节点只有左子树，右子树为空
如图，在这种情况下，我们根据删除节点的位置又可以分出三类：
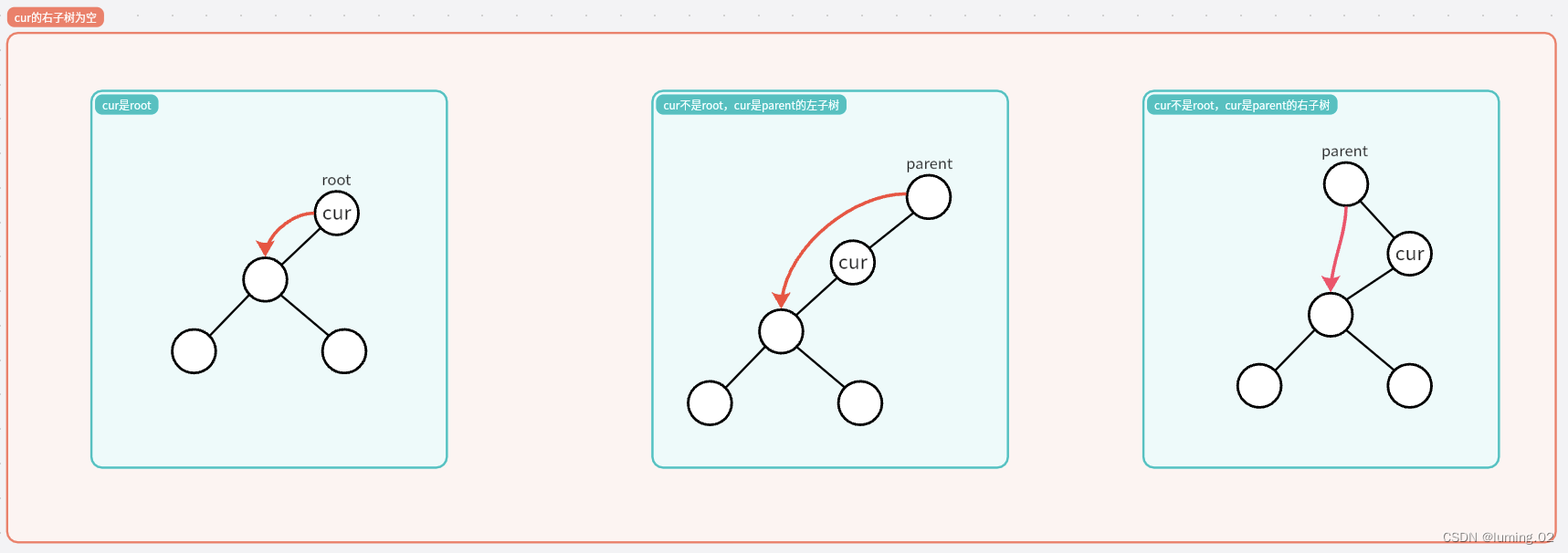
情况一：当删除节点为根节点的时候，因为删除节点没有右子树，所以我们直接将删除节点的左子节点更新为新的根节点，也就是
root = cur.left;情况二：当删除节点为父亲节点的左子节点的时候，因为删除节点没有右子树，所以我们直接让父亲节点的左指针指向删除节点的左子节点，也就是
parent.left = cur.left;情况三：当删除节点为父亲节点的右子节点的时候，因为删除节点没有右子树，所以我们直接让父亲节点的右指针指向删除节点的左子节点，也就是
parent.right = cur.left;3.删除节点左右子树都不为空
在这种情况下，我们往往需要在多个叶子节点中选取一个合适的叶子节点，并且将其替换掉删除节点，最后再将这个叶子节点删除，我们拿下图的情况一举例：
那么我们就需要解决一个问题，如何找到合适的叶子节点，在这里笔者给大家提供一个方法：
- 找删除节点左子树中的最大值
- 找删除节点右子树中的最小值
上述俩中方法选择一种即可，我们随便拿其中一种方法分析举例
假如我们找到了删除节点右子树中的最小值，那他就可以同时满足俩个条件， 他比删除节点中的所有右子树节点都小，又因为他在右子树，所以他也大于删除节点的左子节点，那么就同时满足了成为搜索二叉树节点的俩个条件，即该节点大于左子节点，小于右子节点。
在删除节点的时候，我们也需要使用父亲节点来避免出现空指针异常的情况，就如前文提到的那样。当我们找到删除节点后，其实我们还需要对删除节点的位置进行判断，就像上图的情况二和情况三一样，原因很简单，删除操作需要使用指针操作，如果删除节点在父亲节点的右边，那我们就需要更改父亲节点的右指针指向，反之则要更改父亲节点的左指针指向，因此我们对这种情况还得做出判断。
我们将删除节点总的代码给出如下：
//删除public void remove(int val) {TreeNode cur = root;TreeNode parent = null;//先找到要删除的节点的位置while (cur != null) {if (cur.val < val) {parent = cur;cur = cur.right;} else if (cur.val > val) {parent = cur;cur = cur.left;}else {//找到要删除的节点了removeNode(parent,cur);//调用函数删除节点return;}}}private void removeNode(TreeNode parent,TreeNode cur) {//对节点的状态进行分类if (cur.left == null) {//要删除节点左子树为空树if (cur == root) {root = cur.right;}else if (cur == parent.left) {parent.left = cur.right;}else {parent.right = cur.right;}}else if (cur.right == null) {//要删除节点右子树为空树if (cur == root) {root = cur.left;}else if (cur == parent.left) {parent.left = cur.left;}else {parent.right = cur.left;}}else {//要删除节点左右都不为空TreeNode temp = cur.right;//用来指向叶子节点TreeNode tempParent = cur;//用来指向叶子节点的父节点while (temp != null) {tempParent = temp;temp = temp.left;}//找到了要替换的节点cur.val = temp.val;//替换完成后就删除叶子节点if (tempParent.left == temp) {tempParent.left = temp.right;//删除叶子节点}else {tempParent.right = temp.right;//删除叶子节点}}前半部分是用来找到删除节点，后半部是根据我们的分析对删除节点的情况做出分类判断然后进行删除操作。
搜索二叉树的完整代码实现
为了方便读者使用，我们这里将整个搜索二叉树的完整代码给出：
public class BinarySearchTree {static class TreeNode {int val;TreeNode left;TreeNode right;public TreeNode(int val) {this.val = val;}}public TreeNode root;//查找public boolean search(int val) {TreeNode cur = root;while (cur != null) {if (cur.val == val) {return true;} else if (cur.val < val) {cur = cur.right;} else {cur = cur.left;}}return false;}//插入public void insert(int val) {TreeNode newNode = new TreeNode(val);if (root == null) {root = newNode;return;}TreeNode cur = root;//记录插入节点TreeNode parent = null;//插入节点的父亲节点while (cur != null) {if (cur.val < val) {parent = cur;cur = cur.right;} else if (cur.val > val) {parent = cur;cur = cur.left;}else {//重复元素不予插入return;}}//判断在父亲节点的左边还是右边进行插入if (parent.val < val) {parent.right = newNode;} else {parent.left = newNode;}}//删除public void remove(int val) {TreeNode cur = root;TreeNode parent = null;//先找到要删除的节点的位置while (cur != null) {if (cur.val < val) {parent = cur;cur = cur.right;} else if (cur.val > val) {parent = cur;cur = cur.left;}else {//找到要删除的节点了removeNode(parent,cur);//调用函数删除节点return;}}}private void removeNode(TreeNode parent,TreeNode cur) {//对节点的状态进行分类if (cur.left == null) {//要删除节点左子树为空树if (cur == root) {root = cur.right;}else if (cur == parent.left) {parent.left = cur.right;}else {parent.right = cur.right;}}else if (cur.right == null) {//要删除节点右子树为空树if (cur == root) {root = cur.left;}else if (cur == parent.left) {parent.left = cur.left;}else {parent.right = cur.left;}}else {//要删除节点左右都不为空TreeNode temp = cur.right;//用来指向叶子节点TreeNode tempParent = cur;//用来指向叶子节点的父节点while (temp != null) {tempParent = temp;temp = temp.left;}//找到了要替换的节点cur.val = temp.val;//替换完成后就删除叶子节点if (tempParent.left == temp) {tempParent.left = temp.right;//删除叶子节点}else {tempParent.right = temp.right;//删除叶子节点}}}
}
本次的分享就到此为止了，希望我的分享能给您带来帮助，也欢迎大家三连支持，你们的点赞就是博主更新最大的动力！
如有不同意见，欢迎评论区积极讨论交流，让我们一起学习进步！
有相关问题也可以私信博主，评论区和私信都会认真查看的，我们下次再见
![[机器学习]简单线性回归——最小二乘法](https://img-blog.csdnimg.cn/direct/00356d6433744736bcf023505acb0eb4.png)
