目录
光线追踪
基本的光线追踪算法
Whitted-Style光线追踪
求曲面交点
求三角形交点
Möller Trumbore Algorithm(MT算法)
光线追踪
这里讲一下为什么我们需要光线追踪,主要是因为光栅化没有办法很好的处理全局的光照效果,就像上节课我们说的到软阴影,还有这个毛玻璃一样的反射光,以及这种间接的光照效果,光栅化无法很好处理,虽然光栅化很快,光线追踪很慢,但是光线追踪的效果很好

基本的光线追踪算法
我们首先来定义一下光线
第一,虽然光是波粒二象性的,但是这里我们简单的认为光是沿直线传播的
第二,我们简单的认为两束光相遇的时候不会发生碰撞
第三,光路具有可逆性,就像我能从镜子里面看到你,那么你也能从镜子里面看到我,而且这个过程光的路线是一样的,当你在凝视深渊的时候,深渊也在凝视着你

我们并不知道会有哪些光线会进入我们的视线,但是根据光路的可逆性,从我们人眼发射出的光线所经过的光路同样也是进入我们人眼的光线的光路,那光线追踪具体怎么做呢
第一步,从人眼向投影平面每个像素投射出去一条光线,找到与场景物体的交点,这里考虑遮挡,只找到最近的交点
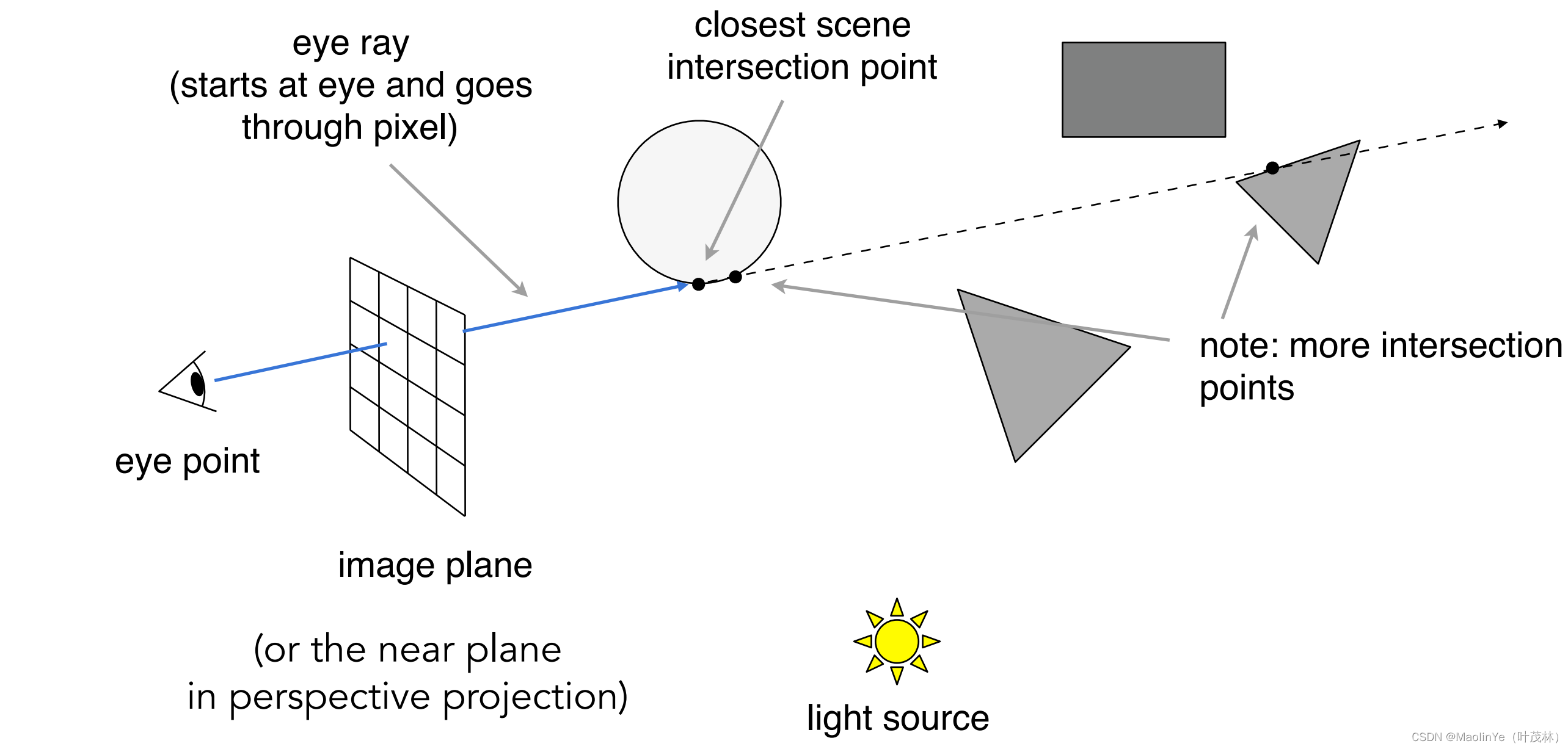
然后将交点和光源连线,根据连线上是否有物体存在判断是否存在阴影,然后用Blinn Phong着色模型计算这个像素的颜色
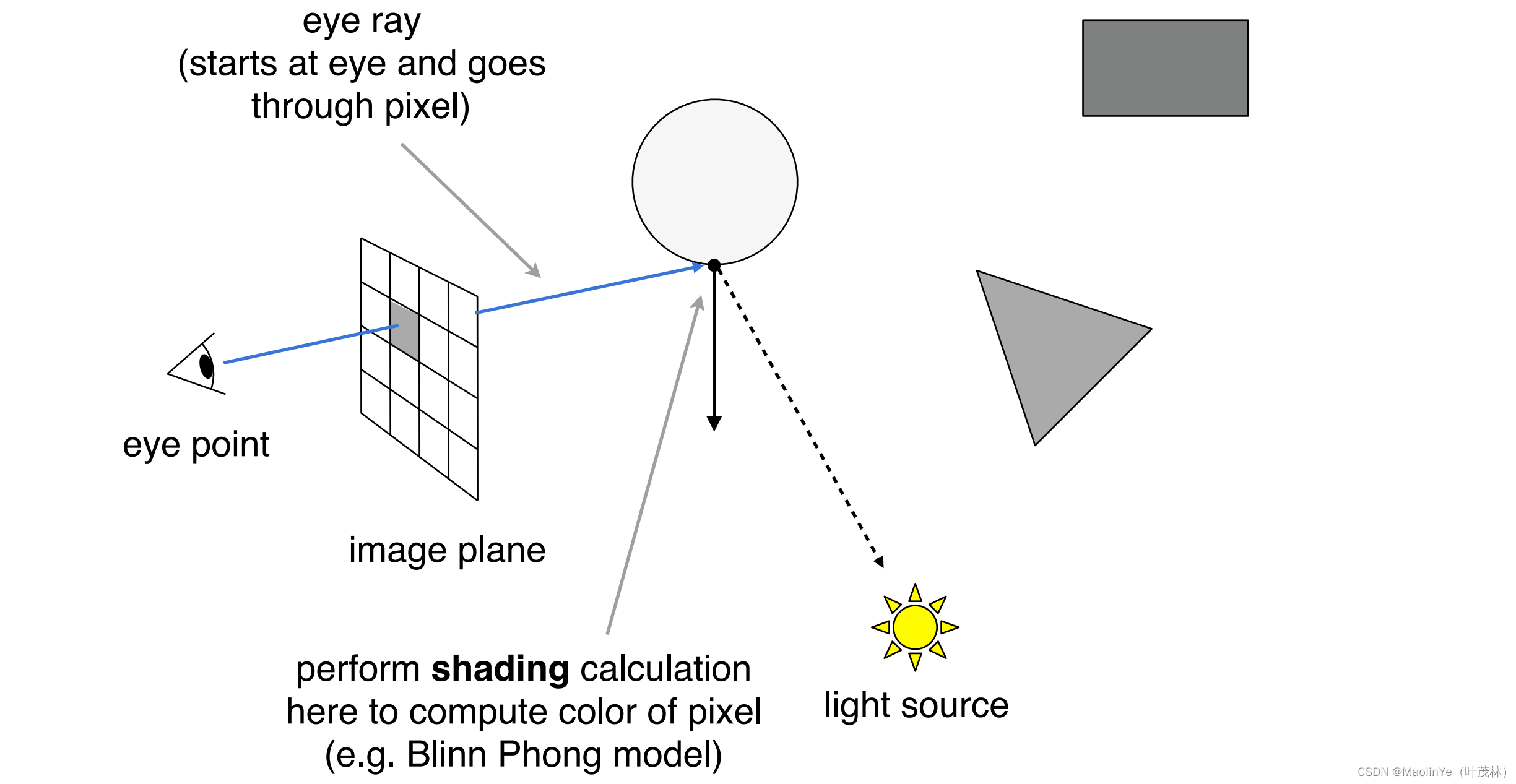 那这个不是和上次shadow mapping一样吗,所以有第二步,叫Whitted-Style光线追踪
那这个不是和上次shadow mapping一样吗,所以有第二步,叫Whitted-Style光线追踪
Whitted-Style光线追踪
找到第一个交点之后并不停止,根据这个物体的材质继续做反射光线
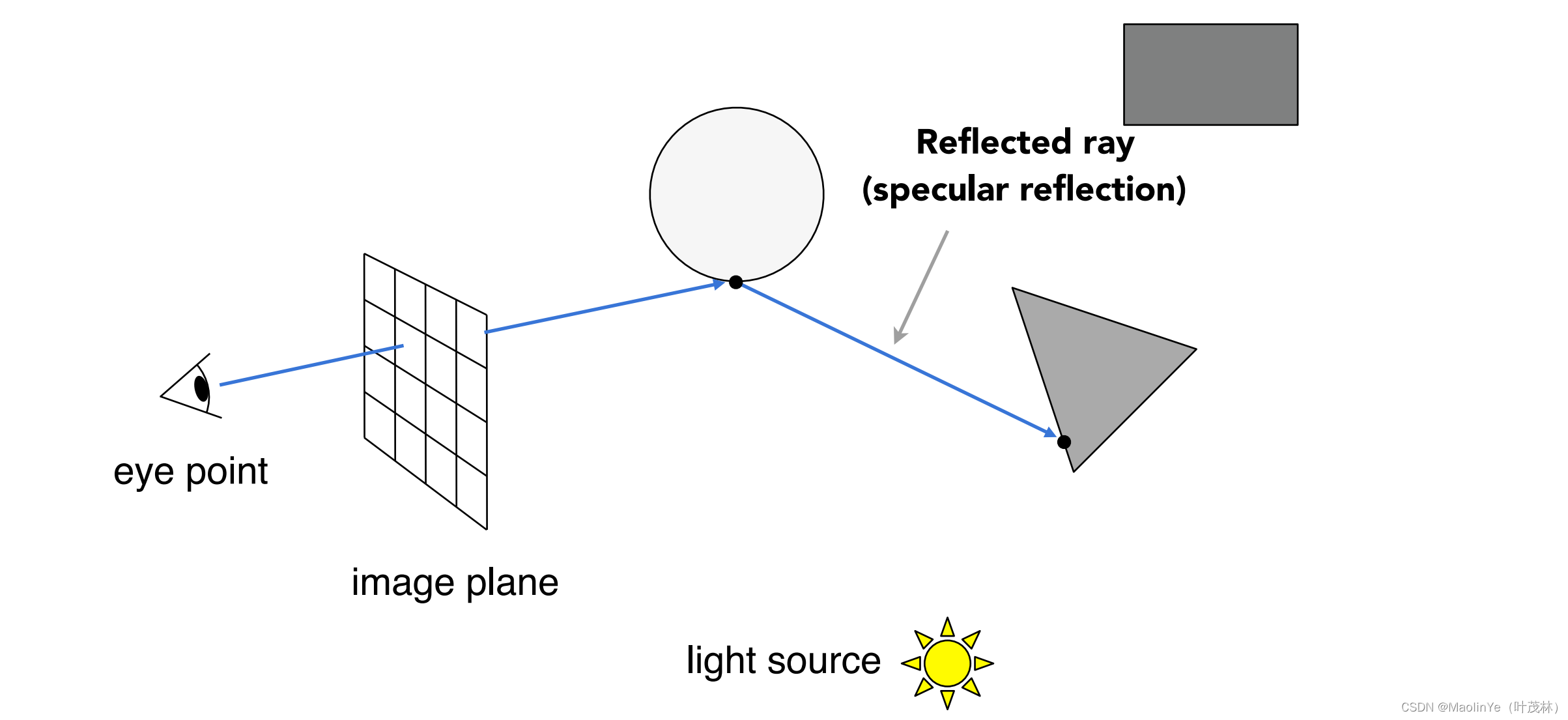
同时也继续做光线的折射

然后计算所有交点的光能量并加权累积,当然这个过程会有光的衰减,然后就可以得到这个像素的全局光照效果了
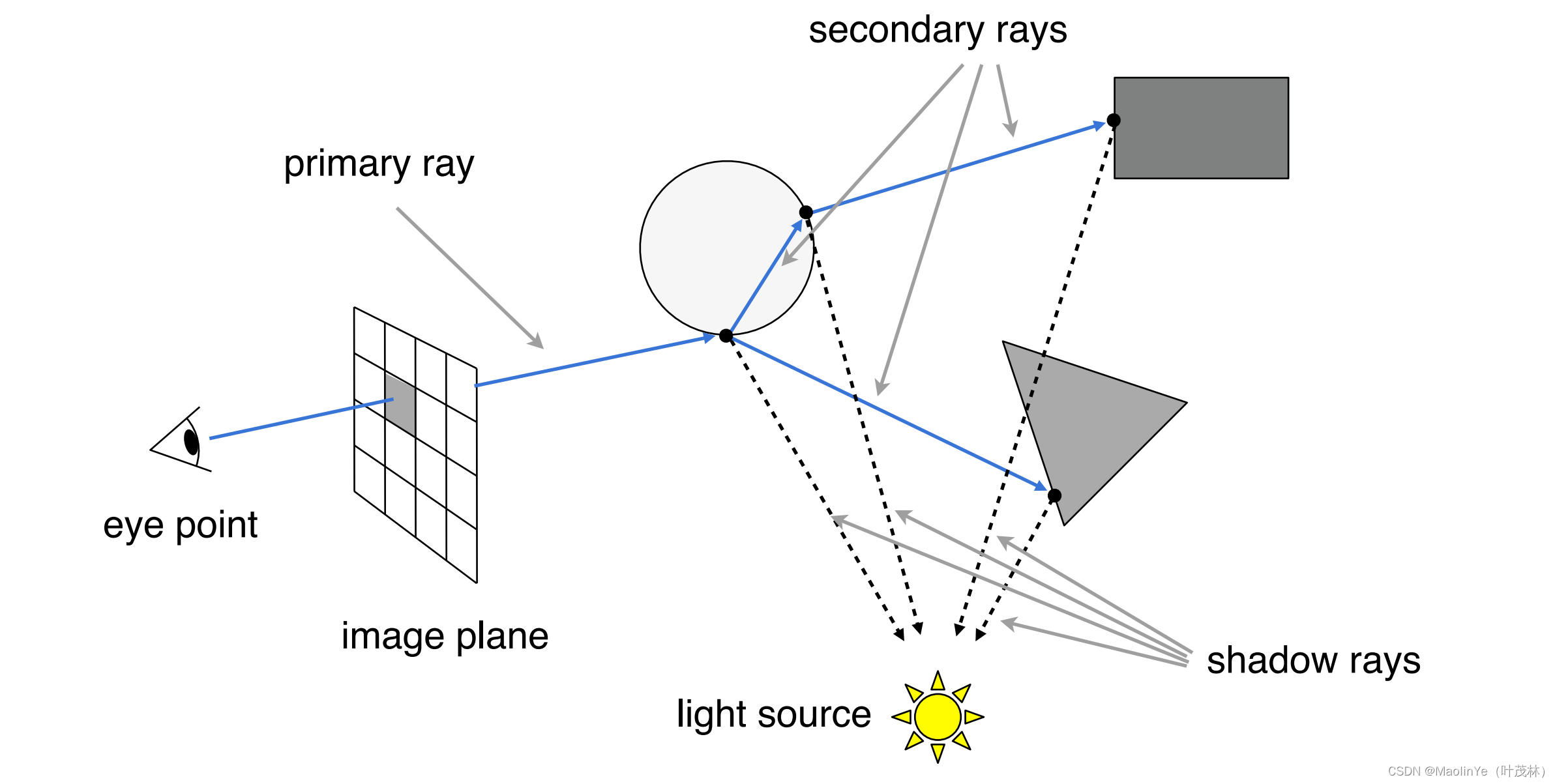
那具体怎么求这些交点呢?
求曲面交点
我们首先来定义一下这个光线的方程,有一个光源点O,然后有这个光线发射的方向d,那么在光线上任意一点就可以通过r(t)=o+td来表示了,其中这个t非负,其实就是射线的表示方程
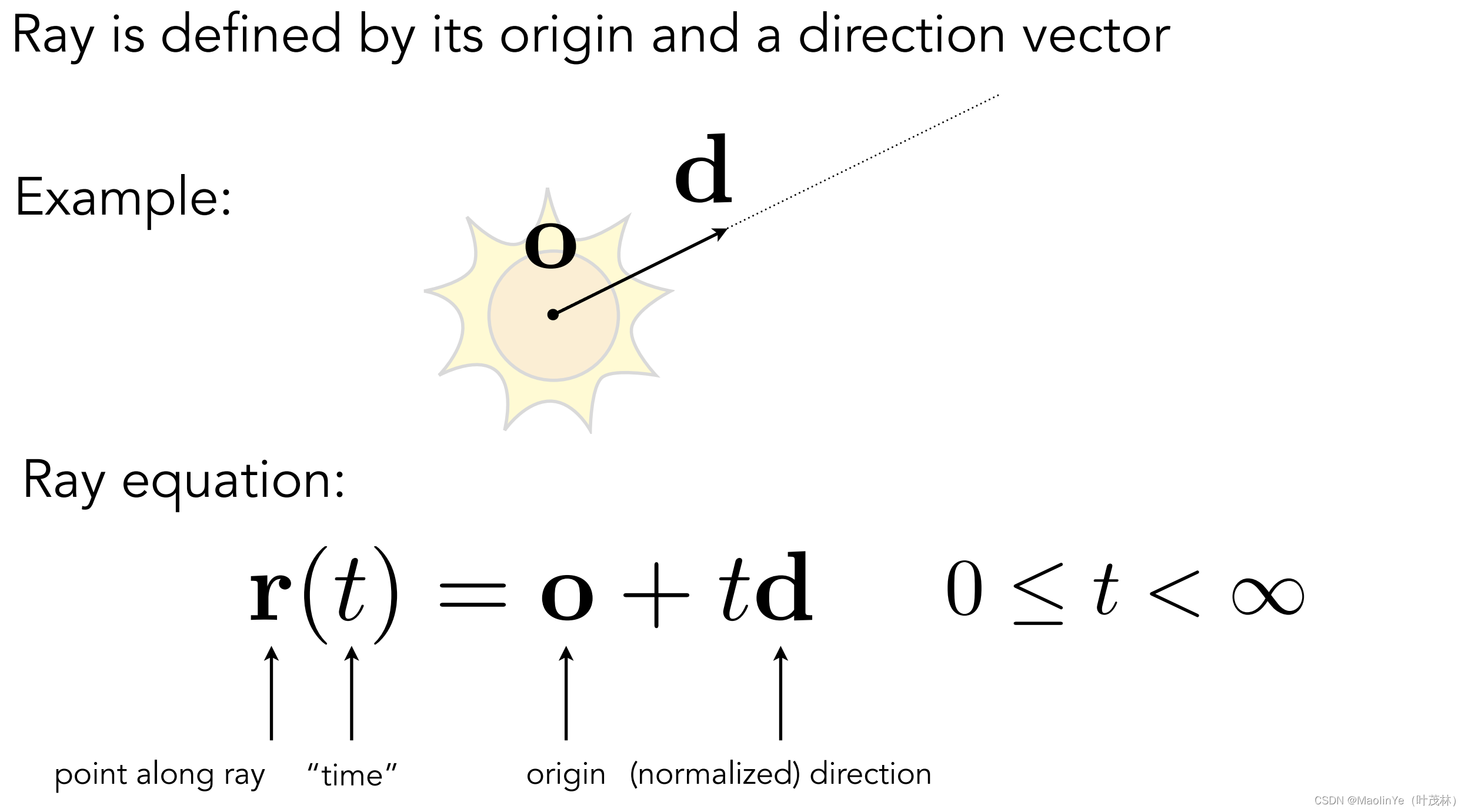
那怎么求交点呢,比如要找光线和一个球面的交点,是不是直接把光线方程代入球面方程就行了,没错,就是这么简单

然后会有相离、相切和相交这几种结果,但是要记得t得非负
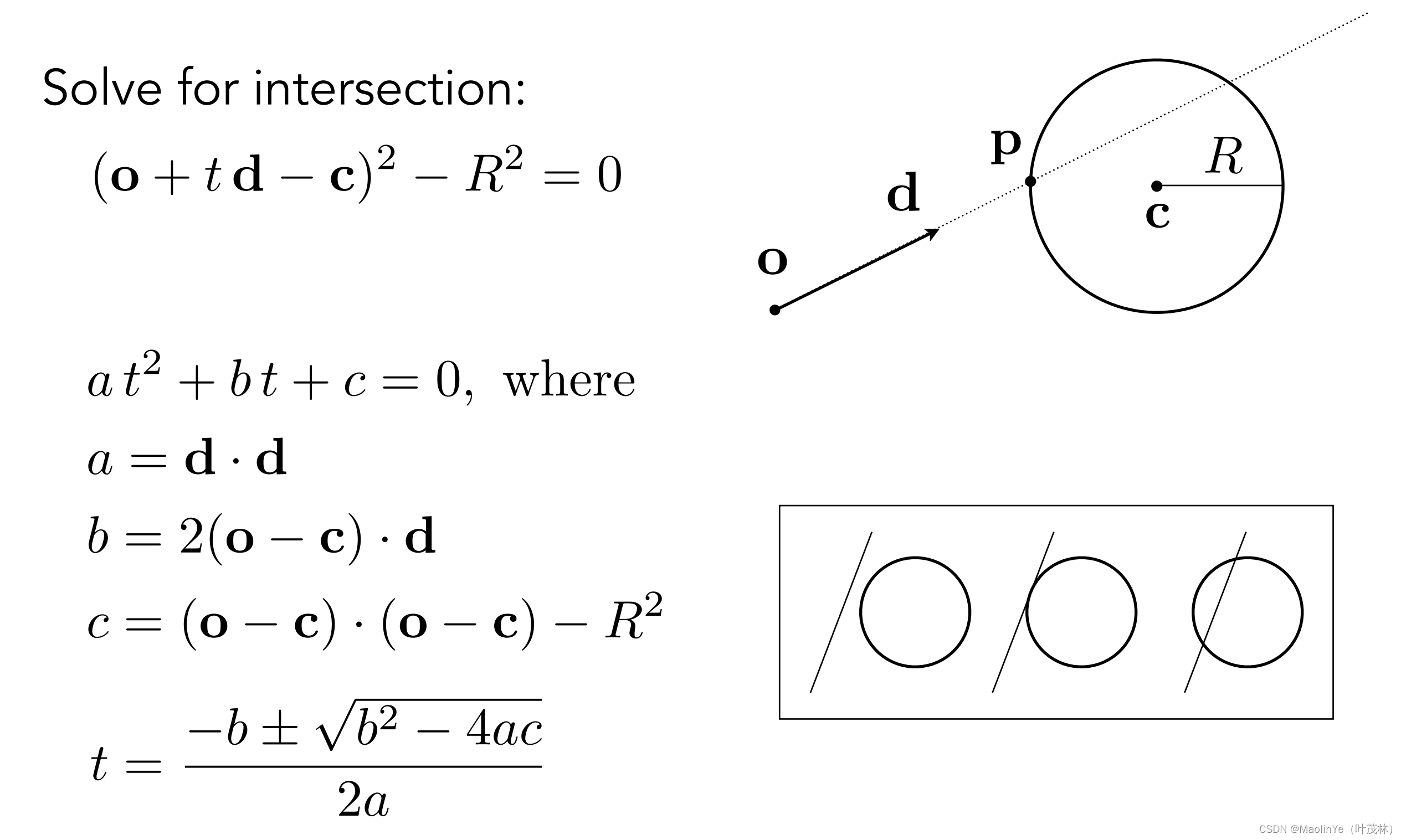 实际也是如此,对于这些隐式表示的曲面就直接将光线方程代入求解
实际也是如此,对于这些隐式表示的曲面就直接将光线方程代入求解

求三角形交点
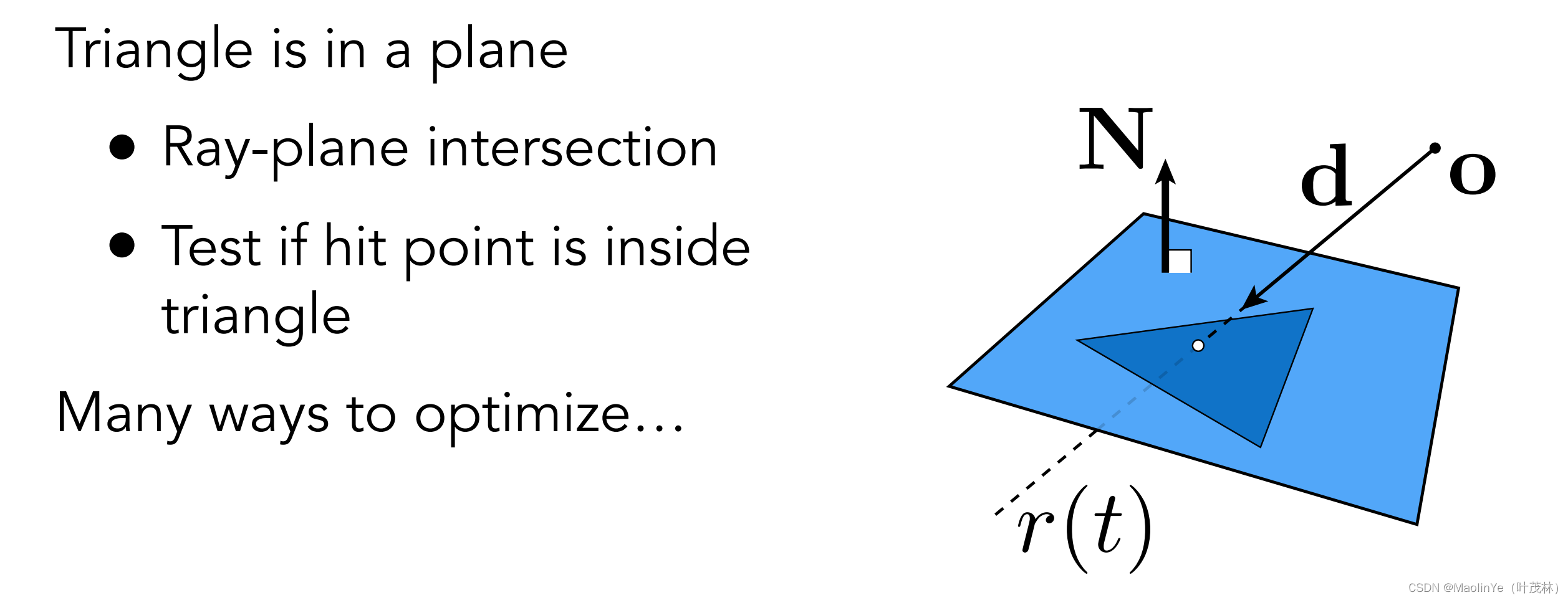
那三角形怎么求光线的交点呢,那这个事情比较复杂,我拆开来做,三角形不是能表示一个平面吗,那我先求光线和平面的交点,再去判断这个交点在不在三角形内,哎判断点在不在三角形内这个我们学过,那问题就是如何求和平面的交点
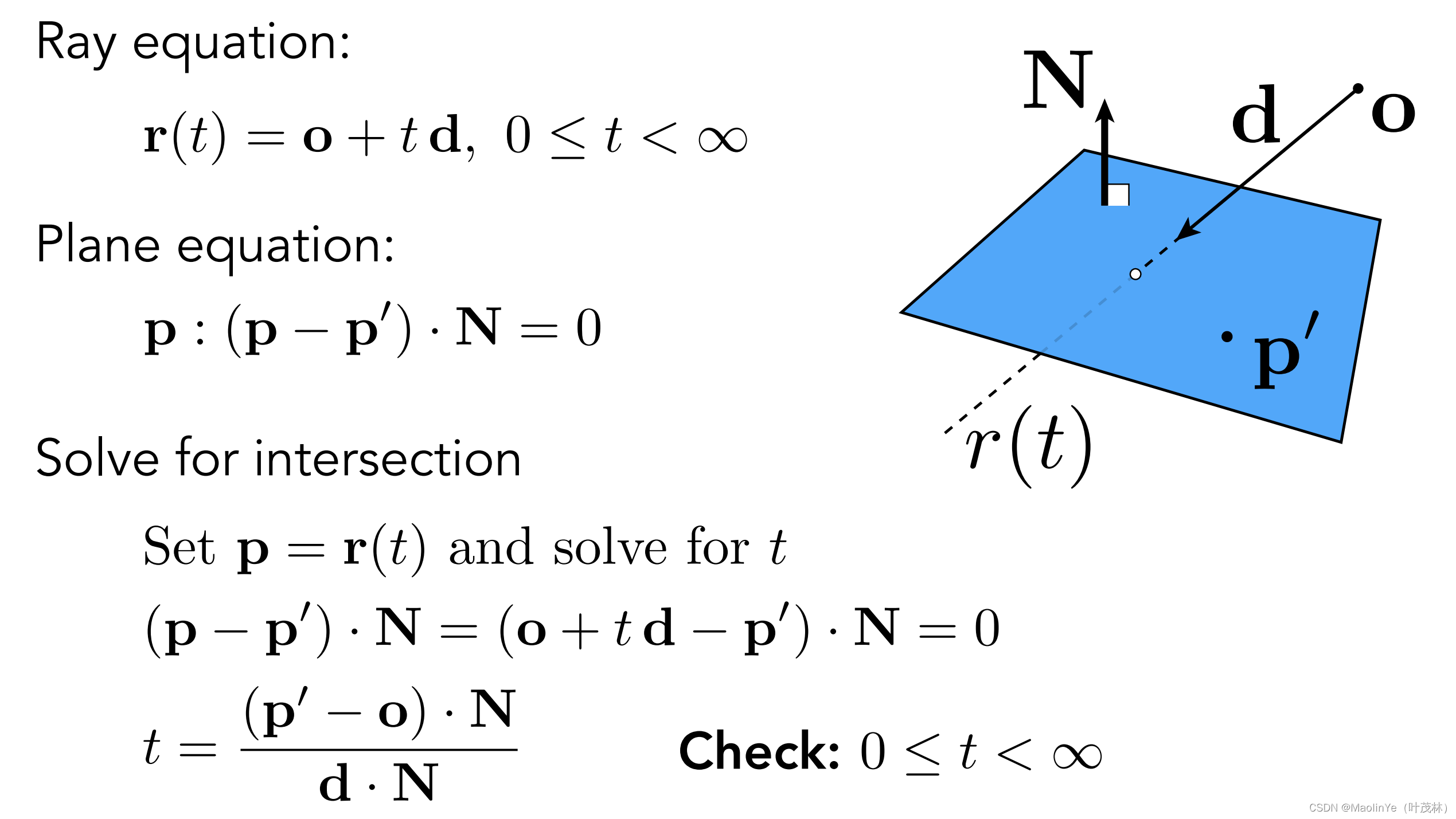
我们先来定义这个平面的方程,对于平面上已知的某个点,还有这个平面的法线,那平面上任意一点和这个点的连线是不是都和法线垂直,那这样就可以写出这个平面的方程(p-p')·N=0

然后我再把光线方程代入平面方程解出t不就行了吗
但是这个是不是算出来之后还得判断这个交点是不是在三角形内部,有没有一算出来就知道和三角形有没有交点的,答案是有
Möller Trumbore Algorithm(MT算法)
我们之前讲插值的时候不是讲过三角形的重心坐标系吗,那如果光线和三角形有交点,那这个交点是不是也会有一个重心坐标,于是就会有下面这个方程
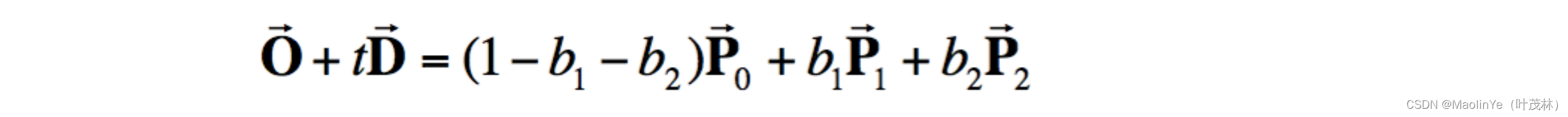
那这里面不是有三个未知数吗,但是我们的O和D实际上是三维的向量,所以这里面其实是三个方程,三个方程三个未知数,可算唯一解
当然如果大家学过这个线性代数的话,这个线性方程组也可以用克莱姆法则算出来
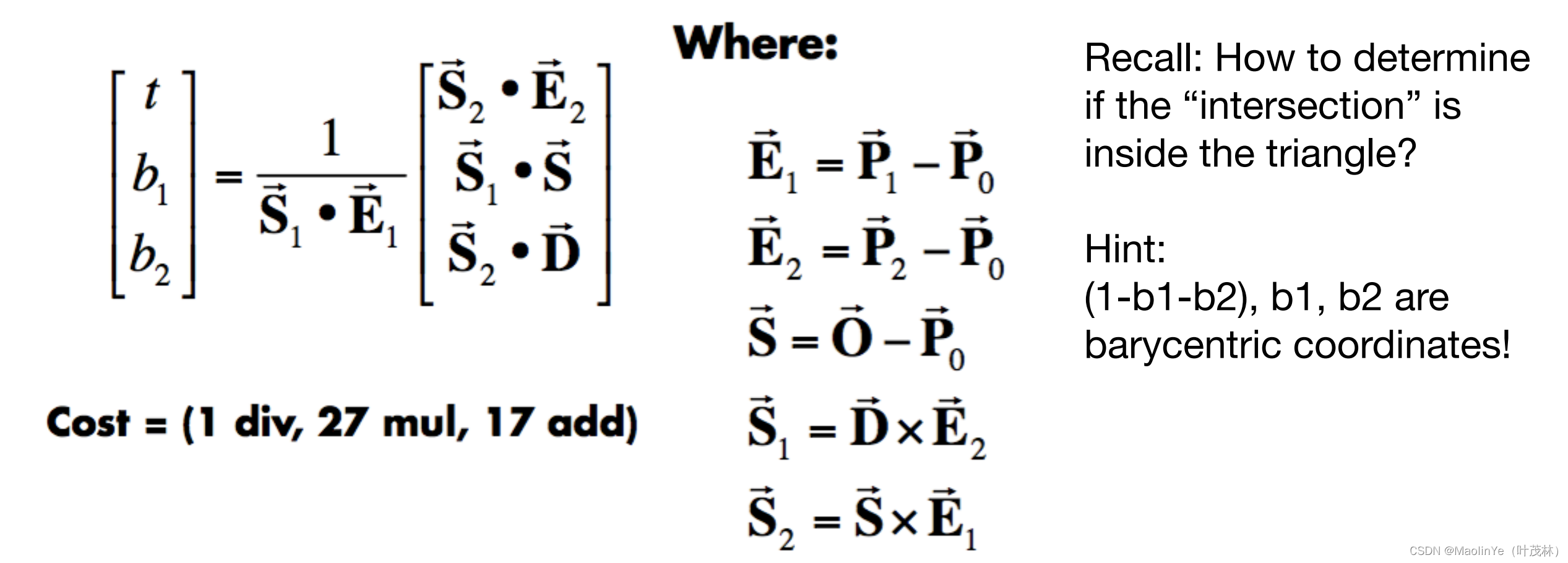
mysqldump)





指针)











