2024.1.28周报

摘要

ABSTRACT

一、文献阅读

1、题目

2、摘要

3、解决的问题

4、算法模型

5、总结

二、PINN方法

三、PINN神经网络源码

总结

摘要

本周我阅读了一篇题目为Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations的文献，论文分两部分，介绍数据驱动解决方案和偏微分方程发现，其次对Burgers方程使用PINN神经网络代码进行了实现，从实验结果可以看出，由干净数据得到的PDE比由带有噪声数据得到的PDE更接近真实值。

ABSTRACT

This week I read a paper titled "Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations". The paper is divided into two parts, introducing data-driven solutions and partial differential equation discovery. Next, the PINN neural network code was implemented for the Burgers' equation. From the experimental results, it can be seen that the PDE obtained from clean data is closer to the true value than the PDE obtained from noisy data.

一、文献阅读

1、题目

题目：Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations

链接：1711.10561.pdf (arxiv.org)

2、摘要

文章中引入物理信息神经网络，通过训练解决监督学习任务，尊重非线性偏微分方程描述的物理定律。论文分两部分，介绍数据驱动解决方案和偏微分方程发现。设计连续时间模型和离散时间模型两类算法，形成新的数据高效通用函数逼近器，自然编码任何潜在物理定律为先验信息。第一部分演示如何使用网络推断偏微分方程解，获得完全可微的物理信息代理模型。

The article introduces the concept of Physical Information Neural Networks, which are neural networks trained to address supervised learning tasks while respecting the physical laws described by nonlinear partial differential equations. The paper is divided into two parts, presenting data-driven solutions and the discovery of partial differential equations. Two types of algorithms are designed based on the nature and arrangement of available data: continuous-time models and discrete-time models. These algorithms form a new class of data-efficient universal function approximators, naturally encoding any potential physical laws as prior information. In the first part, the paper demonstrates how these networks are utilized to infer solutions to partial differential equations, obtaining a physically informed proxy model that is fully differentiable with respect to all input coordinates and free parameters.

3、解决的问题

1、监督学习是机器学习中的一个大类，很多分类问题，回归问题都可以用它来解决。那么，从求解PDE的角度来看，监督学习能发挥什么样的作用呢？

（如何逼近一个函数（算子）一直以来便是数学中的难题。数学家们发展了很多工具来逼近函数，如插值理论，框架，谱方法，有限元等。从逼近论的角度来看，神经网络（Neural Networks）便可以看做一个非线性函数逼近器。我们期望输出一个数据，通过神经网络输出的值可以反应出输入数据的好坏，有效性等，从而有助于我们理解问题。假设我们限制神经网络输出的值是一维的，那么对于 binary classfication 来说，我们可以把大于 0 的分为一类，小于 0 的分为另一类。但是对于一个PDE来说，我们如何来判断输入数据的好坏呢？）
2、机器学习的最新研究在众多科学学科中有了革命性的成果，但在复杂物理、生物或者工程领域中常常因为训练数据采集难度高，限制了机器学习在这些领域的发展，如何在较小训练集的情况下能够达到较高的预测精度呢？

（在很多实际的工程问题中，我们经常会碰到很多预测问题，而当这些预测问题与时间和空间相关时，他们往往会与偏微分方程（PDE）相关，比如台风预报、河流流速流量预测等等。一般来说，主流的求解偏微分方程问题的手段大多采用有限元法。有限元法的基本思想是借助离散化的方法，通过将大问题进行分解，转化成可以简单求解的小问题。那么这种方法有什么缺陷呢？最明显的一个缺陷是，这个方法需要进行离散化，通过将问题区域网格化来进行求解。但是在很多实际的问题中，区域往往并非是规则的、易分的几何区域，此时网格很难生成，基于网格的方法也无法取得很好的效果。除此缺陷外，传统的求解方法还存在着噪声对解的准确性影响很大、高维问题难以求解、由已知的稀疏的观测解很难反推原问题等等。而最近机器学习等数据驱动的方法被证明在解决一些预测问题上有着比较好的效果，我们可以不需要任何物理先验知识，仅仅通过大量的数据去对结果进行预测。这个预测过程自然也绕开了偏微分方程。但是，数据驱动方法也有问题，那就是很多情况下我们无法获得足量且优质的数据。对于有些工程问题，我们进行实验获取数据的成本太高，不足以支撑我们一遍遍进行实验直到获得足够的数据；而在一些工程实践中，我们的设备精度不够，无法支撑我们获得质量足够好的数据。那么一个很自然的想法出现了——能不能将我们已知的一些物理知识和数据驱动的方法相结合呢？）

4、算法模型

模型而所谓的物理神经网络，其实就是把物理方程作为限制加入神经网络中使训练的结果满足物理规律，而这个所谓的限制是怎么实现的？其实就是通过把物理方程的迭代前后的差值加到神经网络的损失函数里面去，让物理方程也“参与”到了训练过程。这样，神经网络在训练迭代时候优化的不仅仅的网络自己的损失函数，还有物理方程每次迭代的差，使得最后训练出来的结果就满足物理规律了。

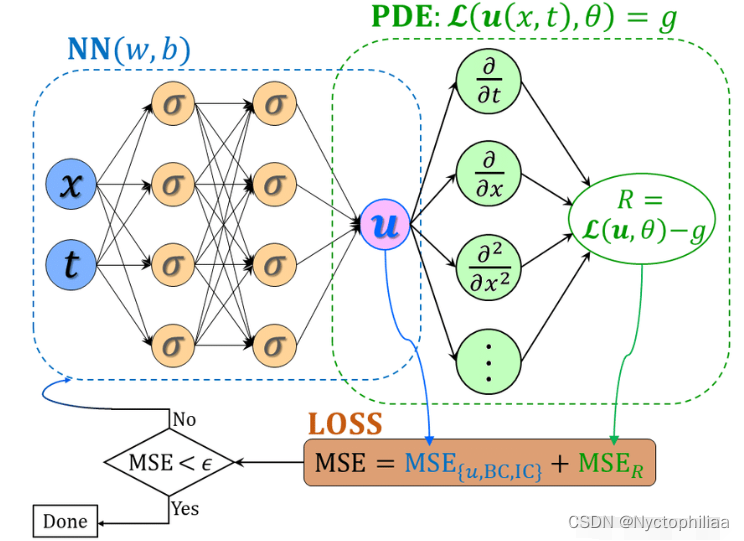
MSE代表均方误差（loss约束的一种）， $eq?MSE_%7B%7Bu%2CBC%2CIC%7D%7D$ 代表数据的拟合情况，能够像传统神经网络一样学习到训练数据样本的分布规律； $eq?MSE_%7BR%7D$ 代表方程的拟合情况，能够学习到数学方程描述的物理定律。（其中u,BC,IC 分别代表微分方程的解、边界条件限制、初始条件限制）

微分方程模型：给定一个非线性PDE ：

用一个具体的例子（Burgers方程，其中参数λ是已知的，故可以在具体的方程中，对应的问题是 Data-driven solutions of nonlinear partial differential equations，就是在讲怎么解 PDEs（Partial Differential Equations））来说明。
主要的想法和步骤：

如果神经网络能很好地求解出PDE的解，那么对于来自初边值的任一个点，其值 $eq?MSE_%7Bu%7D$ 趋于零；对于内部的配置点，因为很好地拟合了微分方程， $eq?MSE_%7Bf%7D$ 趋于零，也就是说，损失函数的值为 0 时，我们便可以说在训练集上每个点都有神经网络的值趋于真实值。
这样便问题便转化为如何优化损失函数。利用神经网络的反向传播机制和L-BFGS便可以求解。

算法模型两类通用解法：
问题明确为：
1、Data-driven solutions of partial differential equations：参数λ已知的时候，如何求的未知的解u(x,t)
2、 Data-driven discovery of partial differential equations：参数λ 未知的时候，如何求解u(x,t)的同时确定参数λ
针对这两个问题，下面两种通用求解算法模型依据数据类型的不同均可进行处理。

1 连续时间模型

$eq?f%28t%2Cx%29%3Du_%7Bt%7D+N%5Bu%5D$

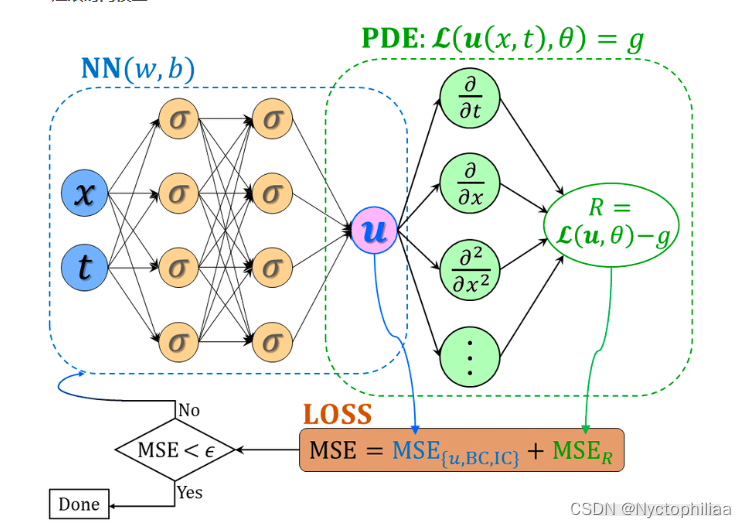
使用神经网络来逼近u(x)和f(x),且这两个网络共享参数,(基于神经网络自动微分的功能，链式法则)

具体操作：首先定义一个网络来你和u(x),然后f(t，x)可以接在u(x,t)的后面再加上一些操作算子,为了优化网络我们定义一个均方损失函数:

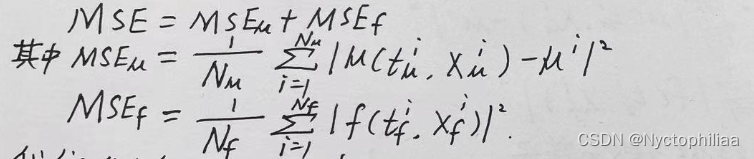
其中上式表示在初始和边界条件处神经网络的拟合值 $eq?u%28t_%7Bu%7D%5E%7Bi%7D%2Cx_%7Bu%7D%5E%7Bi%7D%29$ 与真实值的均方误差；下式表示神经网络与真实物理规律的均方误差。

2 连续时间模型

MSE= $eq?MSE_%7B%7Bu%2CBC%2CIC%7D%7D$ + $eq?MSE_%7BR%7D$ ，，具体来说，之前连续时间模型的输出是一个u，而离散时间模型的输出在上面已经提到了，是一个多输出的神经网络拟合，并且构成了物理信息神经网络，有多个方程。因此，它的MSE= $eq?MSE_%7B%7Bu%2CBC%2CIC%7D%7D$ （多个输出的u，像连续时间模型一样进行求和即可）+ $eq?MSE_%7BR%7D$ （多个R，像连续时间模型一样进行求和即可）。

5、总结

物理信息神经网络是在神经网络通用近似理论的基础上，通过加入偏导数等算子给数值模拟加上了物理约束，从而使得整个网络具有模拟物理规则的作用。关键点在于：通用近似理论 + 物理信息的传递（导数算子+残差构建）+NN的自动微分（AD），简单的全连接神经网络甚至已经能很好地进行通用近似了。

二、PINN方法

PINN的主要思想如下图，先构建一个输出结果为 $eq?%5Cwidehat%7Bu%7D$ 的神经网络，将其作为PDE解的代理模型，将PDE信息作为约束，编码到神经网络损失函数中进行训练。损失函数主要包括4部分：偏微分结构损失(PDE loss)，边值条件损失(BC loss)、初值条件损失(IC loss)以及真实数据条件损失(Data loss)。

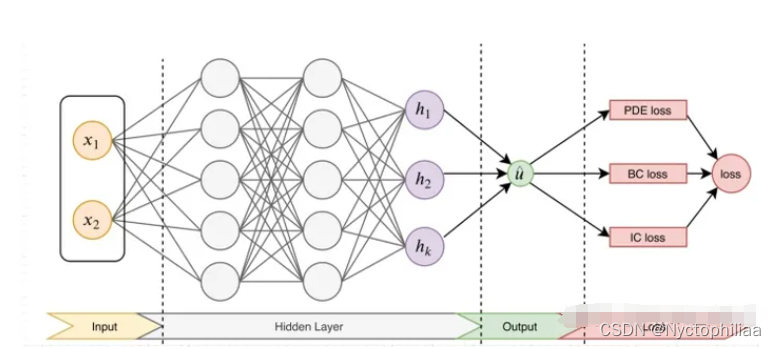
值得注意的是，对于逆问题，即方程中的某些参数未知。若只知道PDE方程及边界条件，PDE参数未知，该逆问题为非定问题，所以必须要知道其他信息，如部分观测点 $eq?u$ 的值。在这种情况下，PINN做法可将方程中的参数作为未知变量，加到训练器中进行优化，损失函数包括Data loss。

三、PINN神经网络源码

1、Physics-informed Neural Networks

下段代码定义了一个深度神经网络（DNN）类，用于创建具有多个隐藏层的前馈神经网络模型。该类通过传递层的维度列表来初始化，然后设置神经网络的各个层，每个隐藏层之间都使用Tanh激活函数。最后，定义了前向传播方法，将输入数据传递到网络中并返回输出结果。

# the deep neural network
class DNN(torch.nn.Module):def __init__(self, layers):super(DNN, self).__init__()# parametersself.depth = len(layers) - 1# set up layer order dictself.activation = torch.nn.Tanhlayer_list = list()for i in range(self.depth - 1): layer_list.append(('layer_%d' % i, torch.nn.Linear(layers[i], layers[i+1])))layer_list.append(('activation_%d' % i, self.activation()))layer_list.append(('layer_%d' % (self.depth - 1), torch.nn.Linear(layers[-2], layers[-1])))layerDict = OrderedDict(layer_list)# deploy layersself.layers = torch.nn.Sequential(layerDict)def forward(self, x):out = self.layers(x)return out

下段代码实现了一个基于物理约束的神经网络（Physics-Informed Neural Network, PINN）模型。它包含了以下关键部分：

初始化和设置参数： 在初始化过程中，提供了数据集（X, u），网络层的结构，以及边界条件（lb, ub）等。同时设置了优化器（LBFGS和Adam）以及损失函数中的参数（lambda_1, lambda_2）。

定义前向网络结构： 通过构建DNN（深度神经网络）类，定义了前向传播过程中的网络结构。这个网络包含了隐藏层、激活函数等。

定义残差函数： 使用神经网络的输出来近似物理方程中的残差。这里使用了自动微分（Autograd）来计算残差，并结合了已知的物理方程形式，其中包含了一些导数的计算。

定义损失函数： 将预测值与实际值的差异以及残差的平方作为损失函数的一部分，目标是最小化损失函数。

训练过程： 使用Adam优化器对网络进行训练，优化损失函数。

预测过程： 使用训练好的模型进行预测，得到输出结果。

# the physics-guided neural network
class PhysicsInformedNN():def __init__(self, X, u, layers, lb, ub):# boundary conditionsself.lb = torch.tensor(lb).float().to(device)self.ub = torch.tensor(ub).float().to(device)# dataself.x = torch.tensor(X[:, 0:1], requires_grad=True).float().to(device)self.t = torch.tensor(X[:, 1:2], requires_grad=True).float().to(device)self.u = torch.tensor(u).float().to(device)# settingsself.lambda_1 = torch.tensor([0.0], requires_grad=True).to(device)self.lambda_2 = torch.tensor([-6.0], requires_grad=True).to(device)self.lambda_1 = torch.nn.Parameter(self.lambda_1)self.lambda_2 = torch.nn.Parameter(self.lambda_2)# deep neural networksself.dnn = DNN(layers).to(device)self.dnn.register_parameter('lambda_1', self.lambda_1)self.dnn.register_parameter('lambda_2', self.lambda_2)# optimizers: using the same settingsself.optimizer = torch.optim.LBFGS(self.dnn.parameters(), lr=1.0, max_iter=50000, max_eval=50000, history_size=50,tolerance_grad=1e-5, tolerance_change=1.0 * np.finfo(float).eps,line_search_fn="strong_wolfe"       # can be "strong_wolfe")self.optimizer_Adam = torch.optim.Adam(self.dnn.parameters())self.iter = 0def net_u(self, x, t):  u = self.dnn(torch.cat([x, t], dim=1))return udef net_f(self, x, t):""" The pytorch autograd version of calculating residual """lambda_1 = self.lambda_1        lambda_2 = torch.exp(self.lambda_2)u = self.net_u(x, t)u_t = torch.autograd.grad(u, t, grad_outputs=torch.ones_like(u),retain_graph=True,create_graph=True)[0]u_x = torch.autograd.grad(u, x, grad_outputs=torch.ones_like(u),retain_graph=True,create_graph=True)[0]u_xx = torch.autograd.grad(u_x, x, grad_outputs=torch.ones_like(u_x),retain_graph=True,create_graph=True)[0]f = u_t + lambda_1 * u * u_x - lambda_2 * u_xxreturn fdef loss_func(self):u_pred = self.net_u(self.x, self.t)f_pred = self.net_f(self.x, self.t)loss = torch.mean((self.u - u_pred) ** 2) + torch.mean(f_pred ** 2)self.optimizer.zero_grad()loss.backward()self.iter += 1if self.iter % 100 == 0:print('Loss: %e, l1: %.5f, l2: %.5f' % (loss.item(), self.lambda_1.item(), torch.exp(self.lambda_2.detach()).item()))return lossdef train(self, nIter):self.dnn.train()for epoch in range(nIter):u_pred = self.net_u(self.x, self.t)f_pred = self.net_f(self.x, self.t)loss = torch.mean((self.u - u_pred) ** 2) + torch.mean(f_pred ** 2)# Backward and optimizeself.optimizer_Adam.zero_grad()loss.backward()self.optimizer_Adam.step()if epoch % 100 == 0:print('It: %d, Loss: %.3e, Lambda_1: %.3f, Lambda_2: %.6f' % (epoch, loss.item(), self.lambda_1.item(), torch.exp(self.lambda_2).item()))# Backward and optimizeself.optimizer.step(self.loss_func)def predict(self, X):x = torch.tensor(X[:, 0:1], requires_grad=True).float().to(device)t = torch.tensor(X[:, 1:2], requires_grad=True).float().to(device)self.dnn.eval()u = self.net_u(x, t)f = self.net_f(x, t)u = u.detach().cpu().numpy()f = f.detach().cpu().numpy()return u, f

2、Configurations

下段代码的作用是为求解Burgers方程提供了必要的数据准备步骤和问题设置。首先，它定义了Burgers方程中的粘性系数（nu），然后设置了神经网络的层结构（layers）。接着，从.mat文件中加载了Burgers方程的数据，包括时间（t）、空间（x）以及准确的解（Exact）。然后，通过网格化的空间和时间网格，构建了输入数据X_star和准确解u_star。最后，设置了问题的边界（lb和ub），即空间和时间的上下界。

nu = 0.01/np.piN_u = 2000
layers = [2, 20, 20, 20, 20, 20, 20, 20, 20, 1]data = scipy.io.loadmat('data/burgers_shock.mat')t = data['t'].flatten()[:,None]
x = data['x'].flatten()[:,None]
Exact = np.real(data['usol']).TX, T = np.meshgrid(x,t)X_star = np.hstack((X.flatten()[:,None], T.flatten()[:,None]))
u_star = Exact.flatten()[:,None]              # Doman bounds
lb = X_star.min(0)
ub = X_star.max(0)

3、Training on Non-noisy Data

下段代码主要用于训练基于物理约束的神经网络模型。首先，它从预先准备的数据集X_star中随机选择了N_u个数据点作为训练集，并相应地选取对应的准确解u_star。然后，利用这些训练数据，构建了一个PhysicsInformedNN类的实例model，并调用了其train方法来对模型进行训练。最后的参数0表示不进行额外的迭代优化，意味着该代码段主要是为了观察模型的初始化状态以及训练时的时间消耗。

%%timenoise = 0.0            # create training set
idx = np.random.choice(X_star.shape[0], N_u, replace=False)
X_u_train = X_star[idx,:]
u_train = u_star[idx,:]# training
model = PhysicsInformedNN(X_u_train, u_train, layers, lb, ub)
model.train(0)

下段代码用于评估训练后模型的性能和参数拟合情况。首先，使用训练好的模型对整个空间和时间范围的数据点进行预测，得到预测值u_pred和残差f_pred。然后，通过计算真实解u_star与预测解u_pred之间的L2范数误差，评估模型的整体拟合性能。接着，使用griddata函数将预测值u_pred插值到整个网格上，得到插值解U_pred。

# evaluations
u_pred, f_pred = model.predict(X_star)error_u = np.linalg.norm(u_star-u_pred,2)/np.linalg.norm(u_star,2)U_pred = griddata(X_star, u_pred.flatten(), (X, T), method='cubic')lambda_1_value = model.lambda_1.detach().cpu().numpy()
lambda_2_value = model.lambda_2.detach().cpu().numpy()
lambda_2_value = np.exp(lambda_2_value)error_lambda_1 = np.abs(lambda_1_value - 1.0) * 100
error_lambda_2 = np.abs(lambda_2_value - nu) / nu * 100print('Error u: %e' % (error_u))    
print('Error l1: %.5f%%' % (error_lambda_1))                             
print('Error l2: %.5f%%' % (error_lambda_2))

4、Visualizations

下段代码用于绘制二维图像，展示了预测的函数u(t,x) 的空间和时间分布情况。通过imshow函数将预测结果U_pred以彩虹色调展示在图像上，同时绘制了训练数据点的位置。在图像中还绘制了三条白色线，表示特定时间截面上的数据。通过修改标签大小、标题大小和标记大小，增强了图像的可读性和美观性。


""" The aesthetic setting has changed. """####### Row 0: u(t,x) ##################    fig = plt.figure(figsize=(9, 5))
ax = fig.add_subplot(111)h = ax.imshow(U_pred.T, interpolation='nearest', cmap='rainbow', extent=[t.min(), t.max(), x.min(), x.max()], origin='lower', aspect='auto')
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.10)
cbar = fig.colorbar(h, cax=cax)
cbar.ax.tick_params(labelsize=15) ax.plot(X_u_train[:,1], X_u_train[:,0], 'kx', label = 'Data (%d points)' % (u_train.shape[0]), markersize = 4,  # marker size doubledclip_on = False,alpha=.5
)line = np.linspace(x.min(), x.max(), 2)[:,None]
ax.plot(t[25]*np.ones((2,1)), line, 'w-', linewidth = 1)
ax.plot(t[50]*np.ones((2,1)), line, 'w-', linewidth = 1)
ax.plot(t[75]*np.ones((2,1)), line, 'w-', linewidth = 1)ax.set_xlabel('$t$', size=20)
ax.set_ylabel('$x$', size=20)
ax.legend(loc='upper center', bbox_to_anchor=(0.9, -0.05), ncol=5, frameon=False, prop={'size': 15}
)
ax.set_title('$u(t,x)$', fontsize = 20) # font size doubled
ax.tick_params(labelsize=15)plt.show()

5、 Identified PDE

fig = plt.figure(figsize=(14, 10))gs2 = gridspec.GridSpec(1, 3)
gs2.update(top=0.25, bottom=0, left=0.0, right=1.0, wspace=0.0)ax = plt.subplot(gs2[:, :])
ax.axis('off')s1 = r'$\begin{tabular}{ |c|c| }  \hline Correct PDE & $u_t + u u_x - 0.0031831 u_{xx} = 0$ \\  \hline Identified PDE (clean data) & '
s2 = r'$u_t + %.5f u u_x - %.7f u_{xx} = 0$ \\  \hline ' % (lambda_1_value, lambda_2_value)
s3 = r'Identified PDE (1\% noise) & '
s4 = r'$u_t + %.5f u u_x - %.7f u_{xx} = 0$  \\  \hline ' % (lambda_1_value_noisy, lambda_2_value_noisy)
s5 = r'\end{tabular}$'
s = s1+s2+s3+s4+s5
ax.text(0.1, 0.1, s, size=25)plt.show()

结果如下：