ascii码表

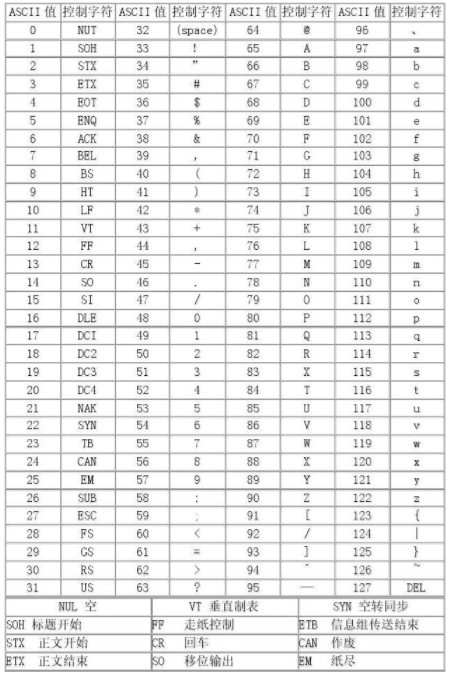
BCD码（Binary-Coded Decimal‎）

BCD码也称二进码十进数
BCD用4位二进制数来表示1位十进制数中的0~9这10个数码
BCD码这种编码形式利用了四个位元来储存一个十进制的数码，使二进制和十进制之间的转换得以快捷的进行。这种编码技巧最常用于会计系统的设计里，因为会计制度经常需要对很长的数字串作准确的计算。相对于一般的浮点式记数法，采用BCD码，既可保存数值的精确度，又可免去使计算机作浮点运算时所耗费的时间。

BCD码可分为有权码和无权码两类。
有权BCD码有8421码、2421码、5421码，
无权BCD码有余3码、余3循环码、格雷码。
每一位没有固定权值的代码称为无权码

有权码-8421码

从左到右的权为 8、4、2、1
以十进制37为例，进行转换：
3=2+1 =(8421码) 0011
7=4+2+1=(8421码)0111

8421BCD码只用了前十个代码，余下的六个代码1010、1011、1100、1101、1110、1111，即为禁止码；

有权码-2421码

从左到右的权为 2，4，2，1
例如：
9（十进制）= 1111（二进制）= 2+4+2+1
5（十进制）= 0101（二进制）= 0+4+0+1

有权码-5421码

从左至右每位的权分别是十进制5、4、2、1
8（十进制）= 1011（二进制）= 5+0+2+1

5421BCD码的禁止码是0101、0110、0111、1101、1110、1111

无权码-余3码

余三码（余3码）是由8421BCD码加上0011形成的一种无权码，由于它的每个字符编码比相应的8421码多3，故称为余三码。
如
1318 十进制 =（0001 0011 0001 1000）8421BCD码=（0100 0110 0100 1011）余3码= 0111 1001 0111 1010

无权码-余3循环码

无权码-格雷码

Gray码（格雷码）也称循环码。

---

---