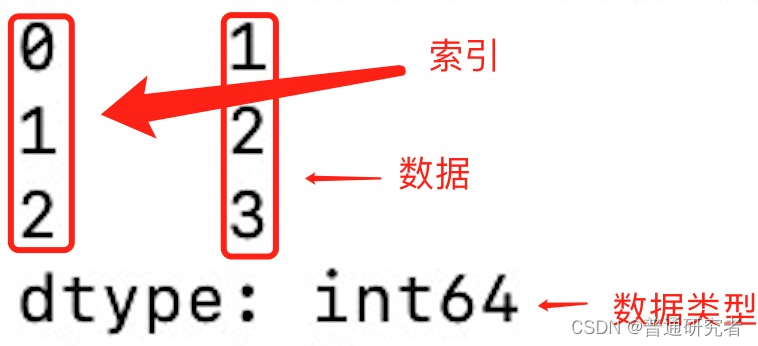
机器学习实际应用时的工程问题与面临的挑战


一、实现细节问题
1.1 训练样本
训练样本与标注对各类机器学习算法和模型的精度影响

训练样本的选择对各类机器学习算法和模型的影响

训练样本的优化

如何进行数据增强?

如何进行数据清洗?

样本的标注对各类机器学习算法精度的影响

样本的对齐

各个类的训练样本不均衡问题怎么解决

1.2 特征预处理
如果特征向量各分量的取值范围相差很大,会影响算法的精度与训练时的收敛

特征预处理方法

将特征向量归一化到单位长度

归一化可以通过学习实现


1.3 模型选择
没有免费的午餐定理

如何选择合适的算法和参数?

剃刀原理

剃刀原理在机器学习中的应用

1.4 过拟合问题

二、安全性问题

2.1 对抗样本

神经网络拟合出的目标函数不连续

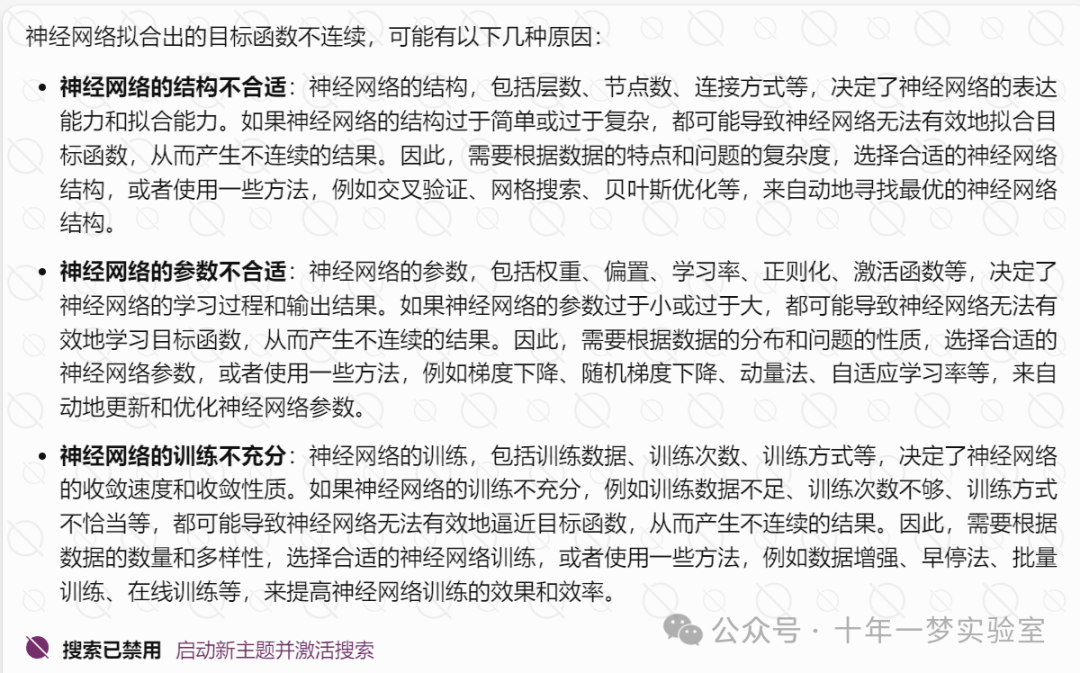
如何找到扰动图像(如何找到一些能够使得机器学习模型产生错误的输出或行为的扰动图像)

什么是对抗样本攻击?
对抗样本攻击是一种在机器学习中的一种安全性问题,它是指利用一些经过特殊设计或修改的数据,来使得机器学习模型产生错误的输出或行为,从而达到攻击或干扰的目的。对抗样本攻击的原因是机器学习模型的泛化能力有限,对于一些看似微小的数据变化,可能会导致模型的输出发生巨大的变化。对抗样本攻击的影响是很严重的,它可能会威胁到机器学习模型的安全性和可靠性,甚至危害到人类的利益和社会的稳定。对抗样本攻击的应用领域很广泛,例如图像识别、自然语言处理、语音识别、生物识别、自动驾驶等。
人工生成对抗样本的方法


2.2 形成原因分析
线性模型拟合数据时哪些情况容易出现对抗样本问题

数据维度过高导致线性模型对抗样本问题

激活函数与对抗样本问题
激活函数是神经网络中的一个重要的组成部分,它决定了神经元的输出和非线性特性。激活函数的选择会影响神经网络的性能和效果,例如准确性、收敛速度、泛化能力等。一些常用的激活函数有线性函数、Sigmoid函数、双曲正切函数、整流线性单元(ReLU)、Leaky ReLU、参数化整流线性单元(PReLU)、指数线性单元(ELU)、斜坡函数(Ramp)等。其中,一些激活函数是不连续的,例如ReLU、Leaky ReLU、PReLU、Ramp等,它们在某些点上的导数为0或无穷大,导致神经网络的输出也不连续。
激活函数与对抗样本问题的关系有以下几个方面:
激活函数的非线性程度:激活函数的非线性程度是指激活函数的输出与输入的非线性关系的强度,它可以用激活函数的导数的变化率来衡量。激活函数的非线性程度会影响神经网络的对抗样本的抵抗能力,一般来说,激活函数的非线性程度越高,神经网络的对抗样本的抵抗能力越强,反之亦然。这是因为,激活函数的非线性程度越高,意味着神经网络的输出对输入的微小变化越不敏感,从而使得对抗样本的生成更困难。例如,Sigmoid函数的非线性程度较高,它的导数在中间区域变化较快,在两端区域变化较慢,这使得Sigmoid函数对输入的微小变化不太敏感,从而使得神经网络的对抗样本的抵抗能力较强。相反,线性函数的非线性程度较低,它的导数在任何区域都是恒定的,这使得线性函数对输入的微小变化非常敏感,从而使得神经网络的对抗样本的抵抗能力较弱。
激活函数的连续性:激活函数的连续性是指激活函数的输出是否在整个输入域内都是连续的,即是否存在任何断点或跳跃。激活函数的连续性会影响神经网络的对抗样本的抵抗能力,一般来说,激活函数的连续性越高,神经网络的对抗样本的抵抗能力越强,反之亦然。这是因为,激活函数的连续性越高,意味着神经网络的输出对输入的微小变化越平滑,从而使得对抗样本的生成更困难。例如,Sigmoid函数和双曲正切函数的连续性较高,它们的输出在整个输入域内都是连续的,没有任何断点或跳跃,这使得Sigmoid函数和双曲正切函数对输入的微小变化比较平滑,从而使得神经网络的对抗样本的抵抗能力较强。相反,ReLU函数和Ramp函数的连续性较低,它们的输出在某些点上存在断点或跳跃,这使得ReLU函数和Ramp函数对输入的微小变化比较突变,从而使得神经网络的对抗样本的抵抗能力较弱。
激活函数的饱和性:激活函数的饱和性是指激活函数的输出是否在某些区域内趋于恒定,即是否存在任何饱和区域。激活函数的饱和性会影响神经网络的对抗样本的抵抗能力,一般来说,激活函数的饱和性越低,神经网络的对抗样本的抵抗能力越强,反之亦然。这是因为,激活函数的饱和性越低,意味着神经网络的输出对输入的变化越敏感,从而使得对抗样本的生成更困难。例如,ReLU函数和Ramp函数的饱和性较低,它们的输出在任何区域都是线性增长的,没有任何饱和区域,这使得ReLU函数和Ramp函数对输入的变化比较敏感,从而使得神经网络的对抗样本的抵抗能力较强。相反,Sigmoid函数和双曲正切函数的饱和性较高,它们的输出在两端区域都趋于恒定,存在饱和区域,这使得Sigmoid函数和双曲正切函数对输入的变化比较不敏感,从而使得神经网络的对抗样本的抵抗能力较弱。

通过哪种方式生成的样本导致大量的神经网络模型出现错分类


三、实现成本问题

3.1 训练样本量
样本的收集和标注问题

小样本深度学习技术


哪些情况适用于半监督学习

3.2 计算与存储成本

四、深度模型优化
深度模型优化的方法

减少存储空间和计算量的方法是对神经网络的模型进行压缩。有哪些实现手段?

剪枝与编码 二值化网络 卷积核分离简述:

4.1 剪枝与编码
剪枝与编码是一种对神经网络模型进行压缩的方法,它包括以下两个步骤:
剪枝:剪枝是指通过删除一些不重要或冗余的模型参数,例如权重、偏置、节点、层等,以减少模型的结构和规模。剪枝的目的是去除模型中的无用或有害的信息,提高模型的性能和精度。剪枝的方法有很多,例如最小化损失函数、最大化信息量、最小化梯度等。剪枝的结果是一个稀疏的模型,即模型中有很多的零值或接近零的值。
编码:编码是指对剪枝后的模型参数进行编码,以减少模型的存储空间和计算量。编码的目的是利用模型的稀疏性,压缩模型的大小和复杂度。编码的方法有很多,例如哈夫曼编码、熵编码、矩阵分解、张量分解等。编码的结果是一个紧凑的模型,即模型中的参数用更少的位数或更简单的形式来表示。
剪枝与编码的优点是可以显著地减少模型的存储空间和计算量,而不影响模型的性能和精度。剪枝与编码的缺点是可能导致模型的不稳定和不可逆。

Deep Compression深度模型压缩技术


稀疏矩阵存储方式 CSR CSC

k 均值算法类中心的初始化三种策略

4.2 二值化网络



二值神经网络的训练算法

二值权重网络

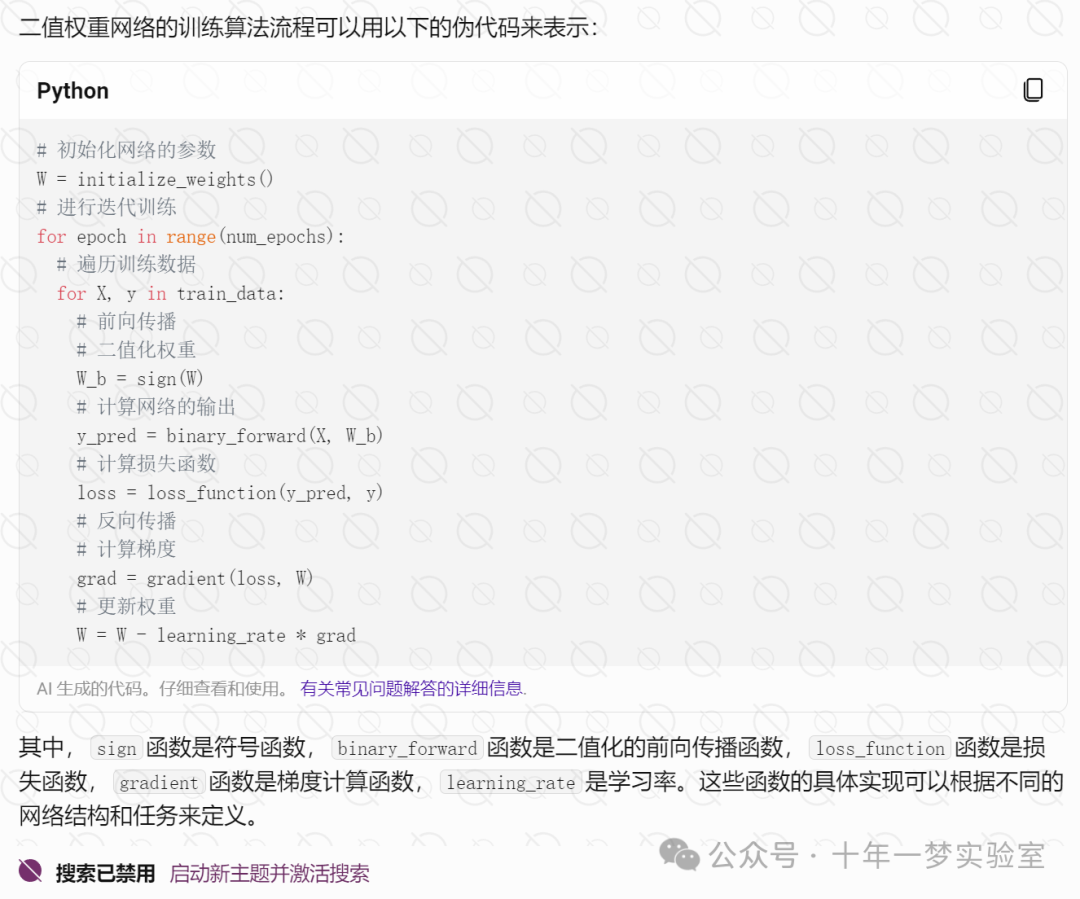
XNOR网络



4.3 卷积核分离