1. Softmax回归–分类问题

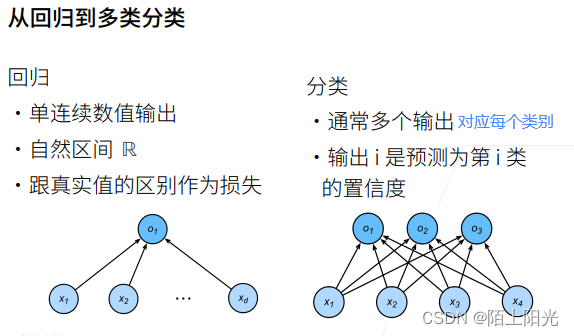
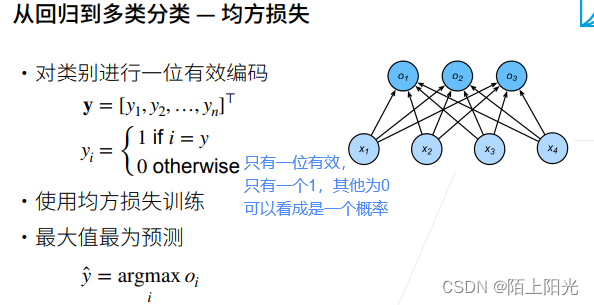
真实y只有一个为1，其他为0，也是概率。

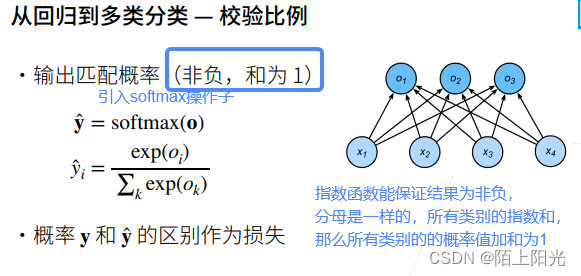
p q假设为离散概率。真实y是有一个类别概率为1，其他为0。

2. 三个常用损失函数

衡量预测值和真实值之间的区别。

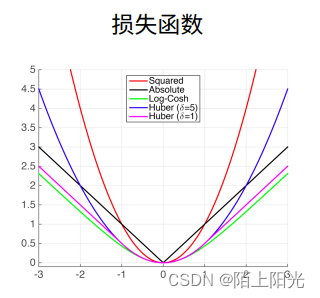
1. 均方损失 L2 Loss

定义：真实值减去预测值的平方再除以2.【除以2为了求导是方便抵消掉系数】
蓝色曲线：二次函数，当y=0， 变化预测值的函数
绿色曲线：似然函数，高斯分布 $e^{-l}$ ?
橙色曲线：损失函数的梯度，是穿过原点的。
梯度下降时，根据负梯度的方向更新参数，导数决定如何更新参数的。当预测值和真实值相差比较大，梯度比较大，参数变化比较大、多；当预测值和真实值相差比较小–靠近原点，梯度越来越小，参数变化的幅度也越来越小。

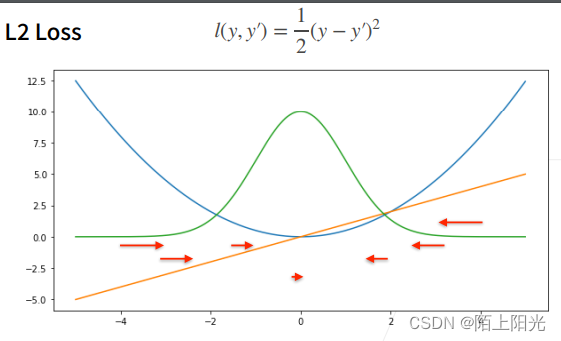
当离原点比较远的时候，不一定想要很大的梯度来更新参数，可以考虑绝对值损失函数。

2. 绝对值损失函数 L1 Loss

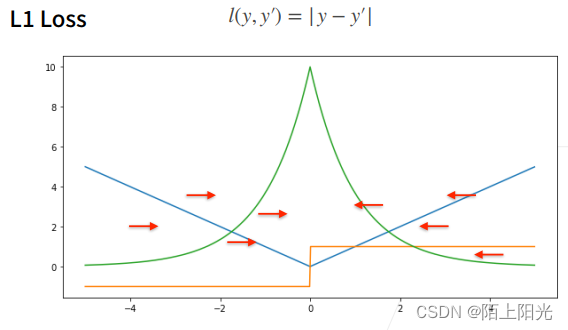
定义：真实值减去预测值的绝对值。
蓝色曲线：损失函数–绝对值函数，当y=0
绿色曲线：似然函数，在原点处有一个很尖的点
橙色曲线：导数–梯度，在大于0，导数为常数1，小于0，导数-1，在0点不可导，导数在（-1,1）之间瞬间变化
当预测值和真实值离得比较远的时候，梯度为常数，权重更新不大，会带来很多稳定性的好处【不管多远，梯度以同样的力度向中间扯】。不好的地方，0点处不可导，从-1到+1的剧烈变化，平滑性差，当预测值和真实值靠的近，优化到了末期，这里可能变得不那么稳定。

3. 两个结合 HUber’s Robust Loss

鲁棒损失
定义：当预测值和真实值差距较大，绝对值大于1的时候，损失函数是绝对值误差，减去1/2是为了和曲线连接起来。
当预测值和真实值差距较小，绝对值小于等于1的时候，是平方误差。
蓝色曲线：损失函数，在正负一之间是平滑的二次函数，之外是直线
绿色曲线：似然函数，很像高斯分布
橙色曲线：在正负一之间，是渐变的；意外是常数。

当预测值和真实值差距较大，梯度用均匀的力度往回拉。
当预测值和真实值差距较小，到了优化末期，梯度会越来越小，保证优化是平滑的，避免出现数值的问题。

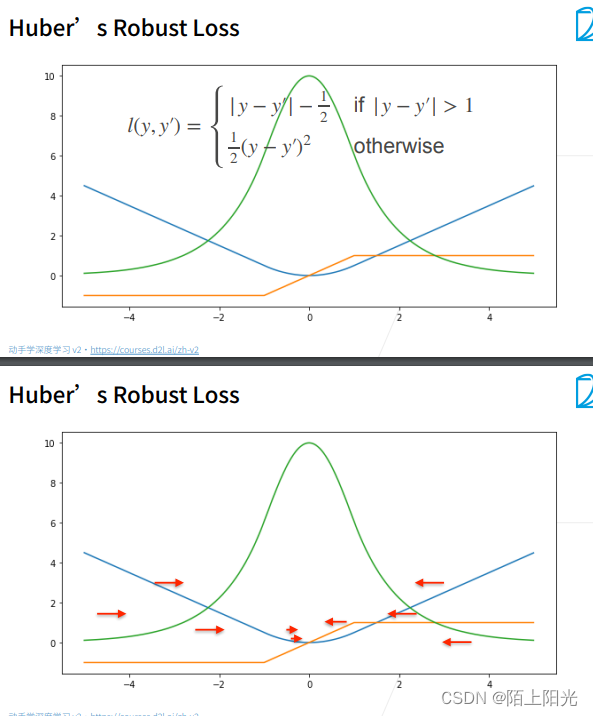
分析损失函数特性：：通过函数形状，梯度形状，分析预测值和真实值差别大 差别小的时候的函数特性。

3. 图片分类数据集

读取多类分类数据集。

4. Softmax回归从零开始实现

5. Softmax回归简洁实现

6. QA

下周再更新。