摘要

存在 theoretical results show that SA and HL are conflicting measures

1 介绍

an algorithm usually performs well on some measures while poorly on others.There are a few works studying the behavior of various measures.Although they provide valuable insights, the generalization analysis of the algorithms on different measures is still largely open.本文 focus on kernel-based learning algorithms which have been widely-used for MLC，this is the first to provide the generalization error bounds for the learning algorithms between these measures for MLC

number of labels (i.e., c) plays an important role in the generalization error bounds

3 Generalization analysis techniques

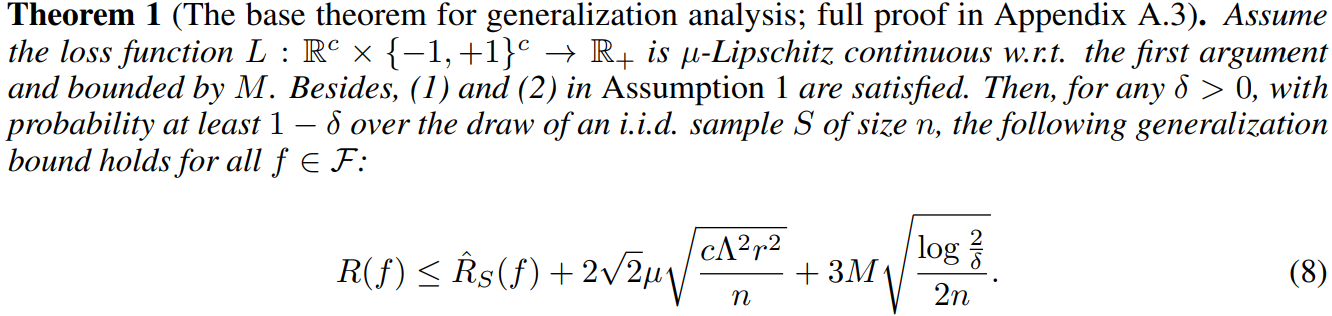
4 Learning guarantees between Hamming and Subset Loss

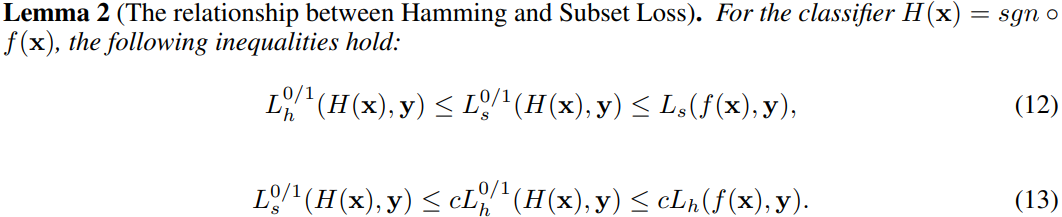
4.1 Learning guarantees of Algorithm $A^h$

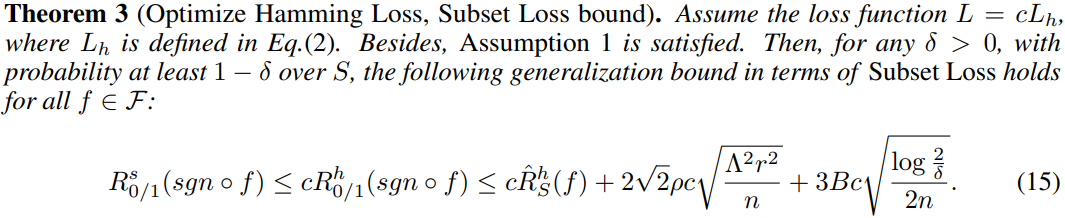
4.2 Learning guarantees of Algorithm $A^s$

4.3 对比

For Hamming Loss，$A^h$ has tighter bound than $A^s$, thus $A^h$ would perform better than $A^s$

5 Learning guarantees between Hamming and Ranking Loss

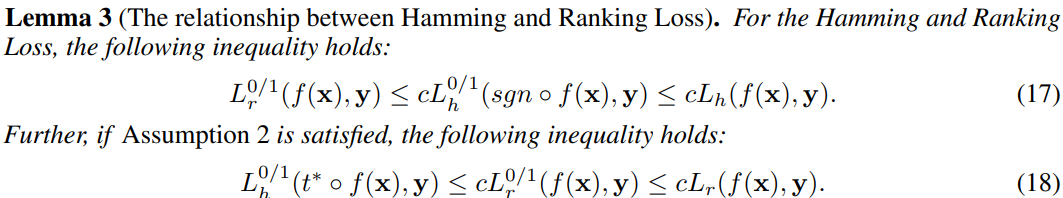
5.1 Learning guarantee of Algorithm $A^h$

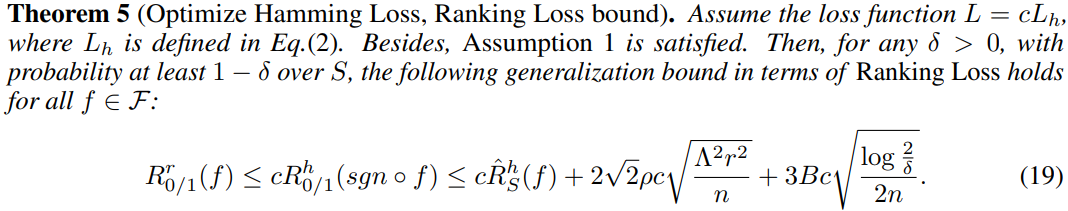
When c is small, $A^h$ can have promising performance for Ranking Loss

5.2 Learning guarantee of Algorithm $A^r$

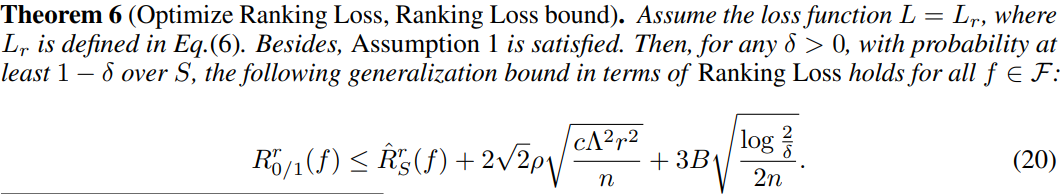
6 实验

for the experiments,the goal is to validate 本文 theoretical results rather than illustrating the performance superiority.For $A^h$ and $A^s$, we take the linear models with the hinge base loss function for simplicity

表2

$A^h$复现结果：
image：$\text{0.192}\pm \text{0.010}$，enron：$\text{0.176}\pm \text{0.013}$，rcv1-subset1：$\text{0.109}\pm \text{0.002}$

表3

复现结果：$\begin{array}{cccc}Dataset& image& enron& rcv1-subset1\\ A^h& \text{0.417}\pm \text{0.021}& \text{0.051}\pm \text{0.021}& ---\\ A^s& ---& ---& \text{0.050}\pm \text{0.004}\end{array}$
默认设置有误差很正常

感悟

第四篇完全复现的论文！