所谓均方误差实际上就是方差

分析：对单词进行编码后，采用聚类方法，可以将单词难度分为三类或者更多，如困难、一般、简单。然后对每一类的单词可视化分析，并描述数据得出结论。

聚类算法较多，在论文中可以使用改进的聚类算法

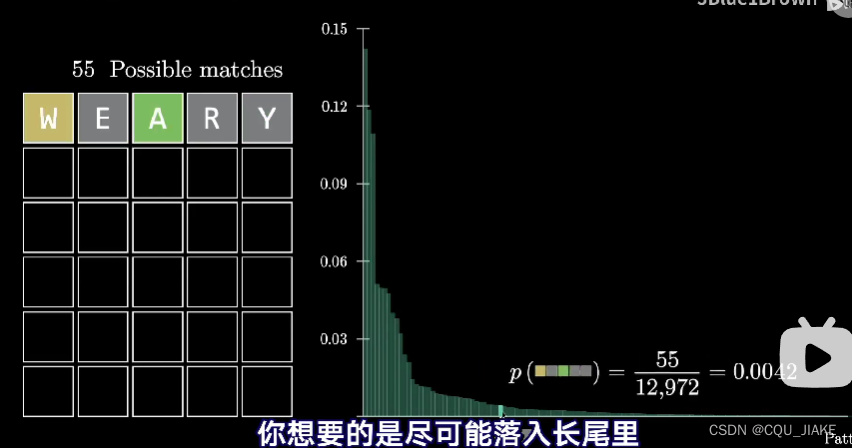
就是说，情况越少，在总的所有可能情况里出现的概率也就越少，出现的话，那么也就越能确定 

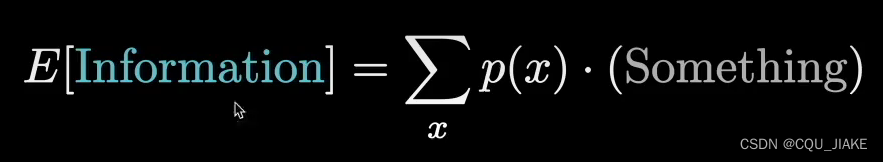
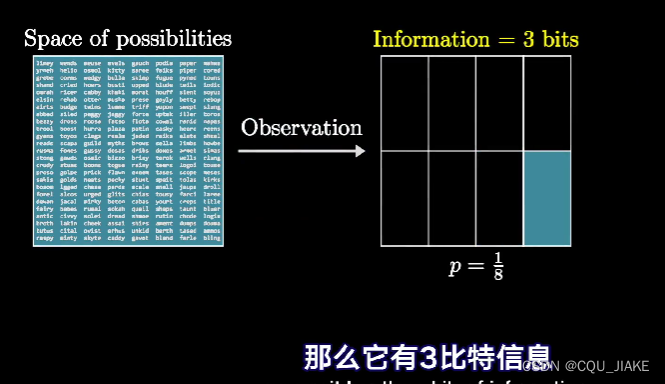
如果所蕴含的信息越多，那么就是经过的判断也就越多，即经过所谓判断（是或不是）也就越多，也就是说，就是用所蕴含的判断次数来确定信息量的大小，划分的越细，所在的格子越小，就认为信息越多，经过二分次数越多，所处的位置精度也就越大

与此同时，信息越多，要想一次就精准确定出这个信息的概率也就越小，即需要正确回答与信息量成正相关的判断次数才可以确定出这个信息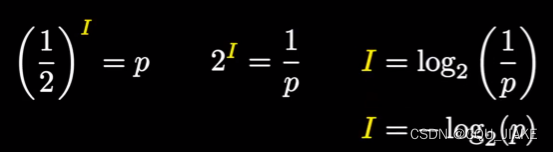

一次观测到了2比特的信息，会将空间缩小到了1/4 ；如果又一次一个3比特的信息，就会在原来1/4的概率空间里，再缩小1/8，变为总的1/32

也就是说筛选掉的错误情况就越少

衡量猜词质量的方式，是计算信息量的期望值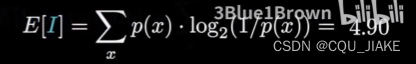

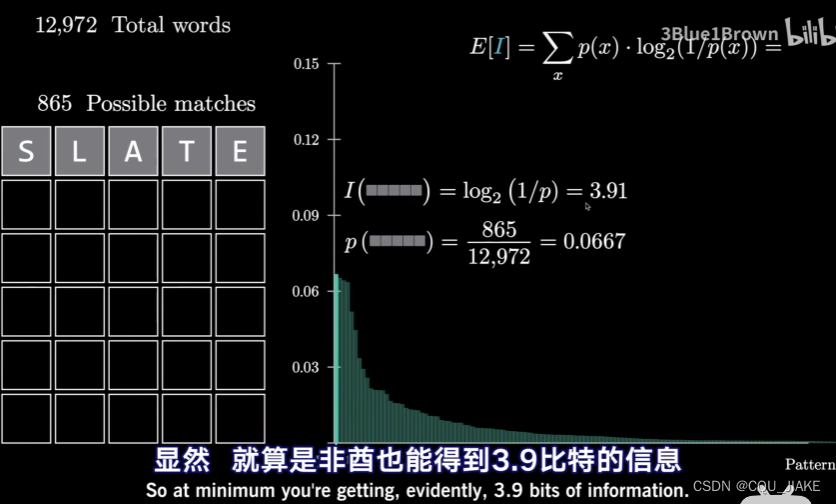
就是说，每个单词都有这么多的出现颜色格子组合的情况，然后依据总的所有的单词数量，可以求出来这个单词所对应的所有出现格子的情况总数，

1.20

熵是信息理论中的一个概念，用于衡量随机变量的不确定性或信息量。在离散随机变量的情况下，熵可以看作是随机变量的平均信息量。

对于一个离散随机变量X，其熵H(X)可以用以下公式表示：

H(X) = -Σ(P(x) * log2(P(x)))

其中，P(x)是随机变量X取值为x的概率。

熵的函数里，只和概率有关，就是概率函数的一个积分

根据这个公式，我们可以看出，当随机变量的取值越均匀分布时，即每个取值的概率都接近于相等时，熵最大。

这是因为，在一个均匀分布的情况下，每个取值的概率都相等，且不确定性最大。而在一个偏向某个取值的分布中，某些取值的概率会更大，从而减少了不确定性，导致熵变小。

因此，越接近于均匀分布，每个取值的概率都相近，每个取值所带来的信息量相似，导致熵变大。而当分布不均匀，某些取值的概率较大，会减少不确定性，使得熵变小。

在信息理论中，信息量是用来衡量传递或表示某个事件或消息所包含的信息多少的指标。

信息量的概念来源于对信息的度量和表示的需要。当我们接收到一条消息或者发生一个事件时，如果这个消息或事件是我们事先不知道的、意外的或者概率较低的，那么它会给我们带来更多的新信息。相反，如果这个消息或事件是我们已经预料到或者概率很高的，那么它会给我们带来较少的新信息。

以二进制的形式来表示信息量是很常见的，其中用比特（bit）来衡量信息量。比特是信息的最小单位，表示一种二元选择（比如是或者不是、真或者假等）。这种表示方法中，每个二元选择都有一个比特的信息量。

信息量的计算可以基于概率来进行。对于一个事件或消息，其信息量可以用以下公式表示：

I(x) = -log2(P(x))

其中，I(x)是事件或消息x的信息量，P(x)是事件或消息x发生的概率。公式中的负号是用来保证信息量为正值。

根据这个公式，我们可以看出，当某个事件或消息的概率很低时，它的信息量会很大；当概率很高时，信息量会减小。因此，信息量可以用来描述一个事件或消息的重要程度或意外程度。
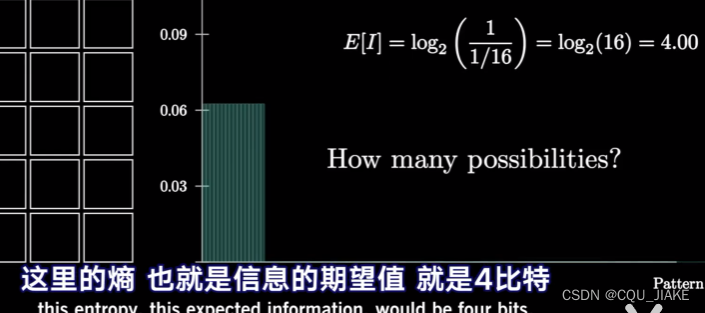
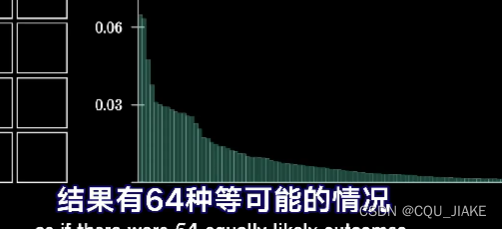